字母系数方程与高次方程的拓展

●章才岔

(温州外国语学校 浙江温州 325000)

方程是一种重要的数学模型，也是一种重要的数学思想.在初中数学竞赛中，含字母系数的方程及高次方程的应用与拓展始终是学生学习上的热点与难点.解决此类问题，常常涉及分类讨论、数形结合等数学思想，用到因式分解、整除和不定方程的解法等有关知识，具有较强的综合性和技巧性.现选竞赛试题为例，谈谈此类方程在竞赛中的拓展应用.

1 变更主元法在解高次方程中的应用

在初中数学竞赛中，对于三次及以上的方程(组)，常常伴随着多个未知数出现.一般情况下，并非每一个字母的最高次都会大于或等于三次，当所求未知数高于三次，而系数字母次数小于或等于二次时，常常可以用变更主元的方法去解此类方程.

例1 已知a≥-6，解关于x的方程

x4-10x3-2(a-11)x2+2(5a+6)x+a2+2a=0.

分析 本题若直接以x为主元解这个方程，次数较高，无从下手．但注意到系数字母a的最高次幂仅为二次，因此可以改变策略，采用变更主元的方法，视a为主变量，x为字母系数，则原方程可化为关于a的一元二次方程，方便求解．此方法将高次方程中的元进行巧妙互换，从而使高次转化为低次，此即转化思想在解题中的应用之一．

解 原方程变形为

a2-2(x2-5x-1)a+(x4-10x3+22x2+12x)=0,

从而Δ= 4(x2-5x-1)2-

4(x4-10x3+22x2+12x)=

4(x2-2x+1),

于是

解得

a=x2-6x或a=x2-4x-2,

即

x2-6x-a=0或x2-4x-a-2=0,

故

注 这是一个典型的变更主元解高次方程的试题，主要运用于转化变量与参数或常数的位置关系，以达到化繁为简的目的，此种解法可以说是一种逆向思维法.

当然，例1中元的变更比较容易，在平时的习题中，同样存在着元用具体数字形式给出的变更方法.

分析 这个方程仅含有一个未知数x，但要求解方程，却非常不易.观察此方程的系数“11”多次出现，故可以将常值11看作一个“未知数”，即通过“常值代换”，进行逆向转换，然后转化成二次方程求解.此题在应用转化思想时，虽然与例1异曲同工，但要将一个常数看作一个新的元时，需要学生们有敏锐的数感，在平时的解题中多观察数式的结构特征，才能触类旁通.

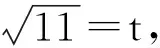
xt2+(2x2+1)t+(x3+1)=0,

解得

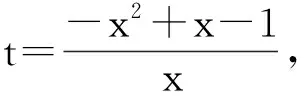
即

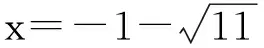
注 高次方程求解的基本思路也是“降次”，因此求解的关键是如何降次及降次的方法.除了常见的配方法、因式分解法、换元法之外，例1和例2给我们提供了解高次方程新的拓展思路.

2 整数解在整系数高次方程中的拓展应用

数学竞赛中的高次多项式或高次方程，很多是在整系数范围内进行研究拓展.对于此类多项式和方程，首先要了解高次方程整数解存在的可能情况，在整数根验证的过程中寻求解题的突破口.

现以首项为1的整系数三次方程为例，探讨在何时会有整数解：对于三次方程x3+px2+qx+m=0，其中p,q,m为整数，若存在整数解c，则c只可能是m的因数.

证明 将c代入原方程得

c3+pc2+qc+m=0，

移项得

m=-c3-pc2-qc，

即

m=c(-c2-pc-q).

因为-c2-pc-q与c及m都是整数，所以c是m的因数．

上述过程说明：整数系数方程x3+px2+qx+m=0的整数解只可能是m的因数．

例3 解方程x3-2x2-4x+3=0.

分析 高次方程的求解，突破口在于降次，本题对于配方、换元等方法显然不适合.而方程左边这种整系数的多项式，让我们联想到是否可以用因式分解进行降次，于是问题可转化为如何寻求多项式的一个因式，而这种因式的寻找，首先从整系数因式开始，即联想方程的整数解.

解 方程x3-2x2-4x+3=0的整数解只可能是3的因数，即1,-1,3,-3.将它们分别代入方程x3-2x2-4x+3=0进行验证,得x=3是该方程的整数解,从而x-3是x3-2x2-4x+3的一个因式,于是

x3- 2x2-4x+3=

x3-3x2+x2-3x-x+3=

x2(x-3)+x(x-3)-(x-3)=

(x-3)(x2+x-1)=0,

例4 已知a是正整数，如果关于x的方程

x3+(a+17)x2+(38-a)x-56=0

的根都是整数，求a的值及方程的整数根.

(2007年全国初中数学联赛试题)

分析 作为高次方程，同时含有字母系数，直接求解不容易.根据已知条件，a是正整数，且方程的根都是整数：一方面可以通过整数根将方程左边因式分解，以达到降次的目的；另一方面，可以通过判别式必须为完全平方数进行因数分解，讨论可能的情况.

解 将方程左边因式分解得

(x-1)[x2+(a+18)x+56]=0,

由题意可知，方程x2+(a+18)x+56=0的根都是整数,从而Δ=(a+18)2-224应为完全平方数.令(a+18)2-224=k2(k是正整数)，则

(a+18+k)(a+18-k)=224.

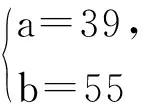
当a=39时，原方程有3个根为1，-1，-56；当a=12时，原方程有3个根为1，-2，-28.

3 整除性在高次方程(组)中的应用

通常关于方程整数解的讨论用到整除知识与分解变形技巧，是初中数学竞赛常考的内容之一.对于整系数高次方程(组)，若已知解为整数，则已经为待定系数增加了一个隐含条件，如何去探求字母系数的关系或求解方程(组)，运用整除性就是常用的有效手段之一.

分析 当遇到高次方程组时，解题的突破口同样在于消元，但如何消元与方程组的形式特征有着极其重要的关系.如本例中，若消去y，则余下就是一个关于x的三次方程，且同时含有3个字母，显然不易求解.第1个方程进行部分因式分解，得y=x3-x(ax+b)，观察第2个方程，通过整体代换可消去a，b这2个待定系数，以下只要根据(x，y)为整数解进行整除性方面的讨论即可.

解 第1个方程可化为

y=x3-x(ax+b)=x3-xy，

即

(1+x)y=x3，

显然方程中x≠-1，因此

因为x,y是整数,所以1+x=±1，即x=0或x=-2.

当x=0时，y=0，此时a,b满足的关系式是b=0(a为任意实数)；当x=-2时，y=8，此时a,b满足的关系式2a-b+8=0.

例6 求使关于x的方程(a+1)x2-(a2+1)x+2a3-6=0的根均为整数的所有整数a.

分析 本题所给方程既是关于x的方程，又是关于a的高次方程.显然题目中以x为主元有利于解题，但同时又隐含着一次方程与二次方程的讨论，解题的基本思路是：

(1)讨论二次项系数的情况:若二次项系数为0，则直接求解判断；若二次项系数不为0，则由韦达定理表示出2个根的和与积.

(2)将2个根之和与积的表示式写成整式与分式和的形式，并且分式的分子一定为整数.

(3)根据整除的性质，可知分式的分母一定是分子的约数，从而求出字母的可能取值.

(4)将字母的可能值分别代入原方程检验,从而确定结果.

解 当a=-1时，原方程变为-2x-8=0，得x=-4，符合要求；当a≠-1时，设方程的2个整数根为x1,x2，则由韦达定理，得

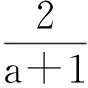
当a=0时，原方程为x2-x-6=0，解得x1=3,x2=-2；当a=1时，原方程为2x2-2x-4=0，解得x3=2,x4=-1；当a=-2时，原方程为-x2-5x-22=0，无实根；当a=-3时，原方程为-x2-10x-60=0，无实根.

综上所述，当a=-1时，方程的整数根为x=-4；当a=0时，方程的整数根为x=3或x=-2;当x=1时，方程的整数根为x=2或x=-1.

4 其他特殊方法在高次方程中的拓展应用

4.1 试根分解

前面，我们了解了在整系数范围下整数根的验根方法，更进一步，在整系数范围下有理根的验根方法如何呢？

试根法即猜根法，是用来试探性地求解一元高次方程的方法，一些比较复杂的因式分解也可以利用试根法来解决(试根法一般适用于整系数多项式的因式分解).具体方法如下：

例7 求一实数p，使得三次方程5x3-5(p+1)x2+(71p-1)x+1=66p的3个根均为自然数.

分析 对比例4，本题中字母系数不明确是否为整数，试根的方法也与例4中整数根的验证有所区别.观察方程的特点，当x=1时，方程2边相等，故66p移到方程左边分解后含有因式(x-1)，进而通过待定系数或综合除法可得

(x-1)(5x2-5px+66p-1)=0

的解为自然数，然后根据韦达定理可知p为方程2根之和，即p是自然数，进而求出p的值.

解 原方程可化为

5x3-5(p+1)x2+(71p-1)x+1-66p=0.

观察知当x=1时，方程左边为0，于是

(x-1)(5x2-5px+66p-1)=0,

因此只要方程5x2-5px+66p-1=0的2个根为自然数即可.因为p是方程5x2-5px+66p-1=0的2个根之和,所以p是自然数.设

Δ=(5p-132)2-17 404=n2(n∈N*),

则

(5p- 132+n)(5p-132-n)=17 404=

22×19×229.

又因为5p-132+n，5p-132-n同奇偶,所以

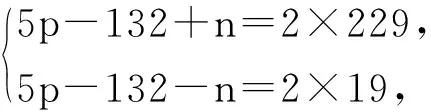
解得

p=76.

4.2 公式变形

变形法主要是对方程中具有特殊形式的式子，通过公式变形转化为具有同一形式或相同特点的式子，进而采用整体或换元的方法使方程降次，再求解的方法.常用的变形式有：

(x+y)2=(x-y)2+4xy；

x2+y2=(x+y)2-2xy=(x-y)2+2xy；

a3+b3=(a+b)[(a+b)2-3ab]；

a3+b3+c3=3abc,其中a+b+c=0.

例8 关于x的方程x4+(k-1)x3+kx2+(k-1)x+1=0没有实数根，求实数k的取值范围.

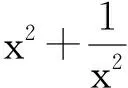
即可采用换元的方法使原方程降次.

解 原方程2边同除以x2，得

y2+(k-1)y+k-2=0，

即

(y+1)[y+(k-2)]=0,

从而y=2-k或y=-1(舍去).要使原方程无解，则

-2

即

-2<2-k<2,

故k的取值范围是0

4.3 零点判断

零点法，就是根据零点存在性定理，当函数在某一闭区间[a,b]上连续，且f(a)·f(b)<0，2个端点值符号相反说明图像必穿过x轴，因此在(a,b)上必有一个零点.

例9 三次方程x3+x2-2x-1=0的根不可能在的区间为

( )

A．(-2,-1) B．(-1,0)

C．(0,1) D．(1,2)

分析 本题属于函数零点存在性定理的简单应用.若去求方程的解，显然不容易也不必要，可令f(x)=x3+x2-2x-1，则函数f(x)在R上连续，然后结合零点存在性定理即可求解.

解 设f(x)=x3+x2-2x-1，则f(x)在R上连续.因为f(-2)=-1<0，f(-1)=1>0,所以函数f(x)在区间(-2,-1)内存在零点，即方程x3+x2-2x-1=0有一个根在区间(-2,-1)内.

同理可得f(0)=-1<0，f(1)=-1<0，f(2)=7>0,因此原方程的3个根分别在区间(-2,-1)，(-1,0)，(1,2)内.

当然，字母系数方程与高次方程作为初中数学竞赛内容的一个部分，其可拓展的宽度与深度方面还有很多.本文仅选取较为常见的一些试题，通过对问题的剖析求解，帮助读者在梳理归纳的过程中，进一步拓展探究，总结方法，达到把握初中数学竞赛试题的脉络.