活跃在竞赛中的几何计数问题
●卢国兴
(桐庐中学 浙江桐庐 311500)
几何计数问题主要是指与几何有关的计数问题,由于该类问题往往蕴含着“形”的美妙与“数”的严谨,因此倍受竞赛命题者的青睐.
几何计数问题的内容比较别致,富于变化.如果自己不能理清思路,寻找到一种合适的解法,就很难得到正确的答案.以下笔者结合一些数学竞赛试题,介绍几种典型的解法.
1 直接分类枚举
当对于原问题中的各种情形一时无法统一处理,并且注意到结论不是很庞大的数字时,不妨采用分类枚举法.“直接分类枚举”是一种最简单、最基本的计数方法.
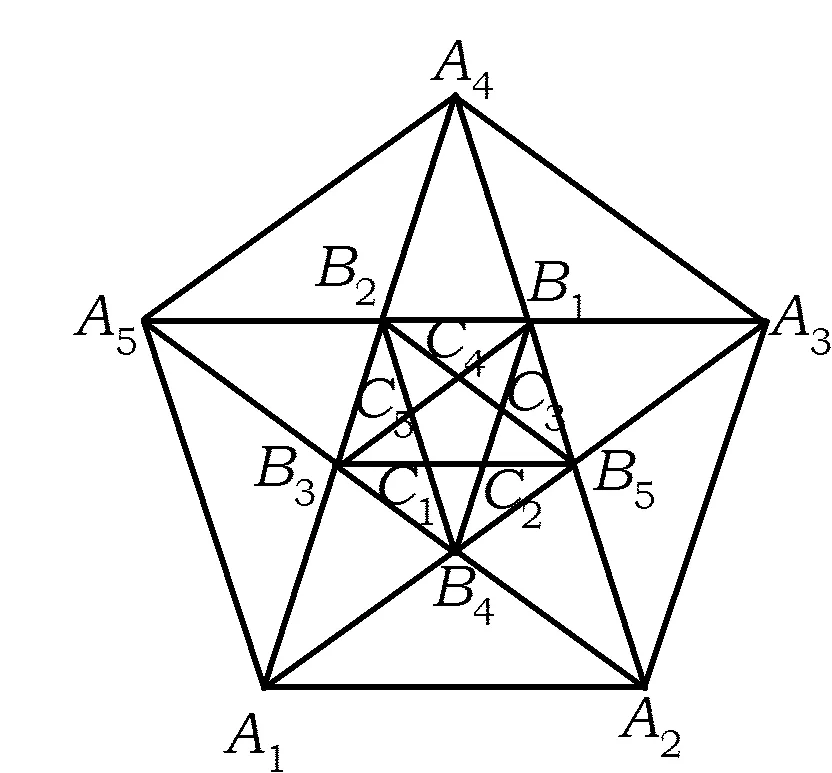
图1
例1 联结正五边形A1A2A3A4A5的对角线交出另一个正五边形B1B2B3B4B5,再次联结正五边形B1B2B3B4B5的对角线,又交出一个正五边形C1C2C3C4C5(如图1),以图中线段为边的三角形中,共有等腰三角形
( )
A.50个 B.75个 C.85个 D.100个
(2005年全国高中数学联赛江西省初赛试题)
解 以A1为2条腰公共点的等腰三角形有6个:△A1A2A5,△A1B3B4,△A1B2B5,△A1A3A4,△A1A2B5,△A1A5B2;
以B1为2条腰公共点的等腰三角形有9个:△B1A3A4,△B1B2B5,△B1B3B4,△B1C3C4,△B1B2C5,△B1C2B5,△B1A2A5,△B1A3B4,△B1A4B3;
以C1为2条腰公共点的等腰三角形有2个:△C1B3B3,△C1B2B5.
由于图1中没有等边三角形,故每个等腰三角形的2条腰恰有一个公共顶点.因此,由对称性可知共有等腰三角形5×(6+9+2)=85个.
例2 作正四面体每个面的中位线,共得12条线段,在这些线段中,求相互成异面直线的“线段对”的个数.
解 任取一条中位线AB,AB所在的侧面没有与AB异面的线段;含点A的另一个侧面恰有一条中位线与AB异面;含点B的另一个侧面也恰有一条中位线与AB异面;不含点A,B的侧面恰有2条中位线与AB异面;因此与AB异面的中位线共有4条,即含有线段AB的异面“线段对”共有4个,于是得到异面“线段对”共有12×4=48个(其中有重复).
但每一个异面“线段对”中有2条线段,故恰好被计算了2次,因此,得到48÷2=24个异面“线段对”.
在直接分类枚举时,必须注意无一重复、无一遗漏,要有规律地进行.
2 运用2个原理
分类计数原理与分步计数原理是解决组合计数问题的2种基本思想方法,是解决计数问题的基础.合理运用2个原理可以顺利解决一些简单的几何计数问题.
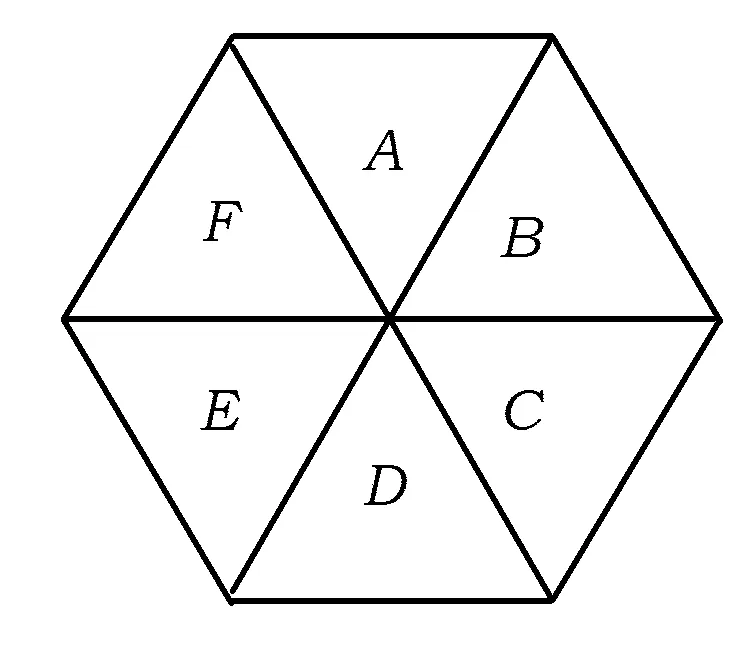
图2
例3 在一个正六边形的6个区域中栽种观赏植物(如图2),要求在同一个区域中种同一种植物,相邻的2个区域种不同的植物.现有4种不同的植物可供选择,则有______种栽种方法.
(2001年全国高中数学联赛试题)
解 将6个区域依次标上字母A,B,C,D,E,F,按A,C,E种植植物的种数进行讨论:
(1)若A,C,E种同一种植物,有4种种法.当A,C,E种植后,B,D,F可从剩余的3种植物中各选一种植物(允许重复),各有3种方法.此时共有4×3×3×3=108种种植方法.
根据分类计数原理,共有N=108+432+192=732种栽种方案.
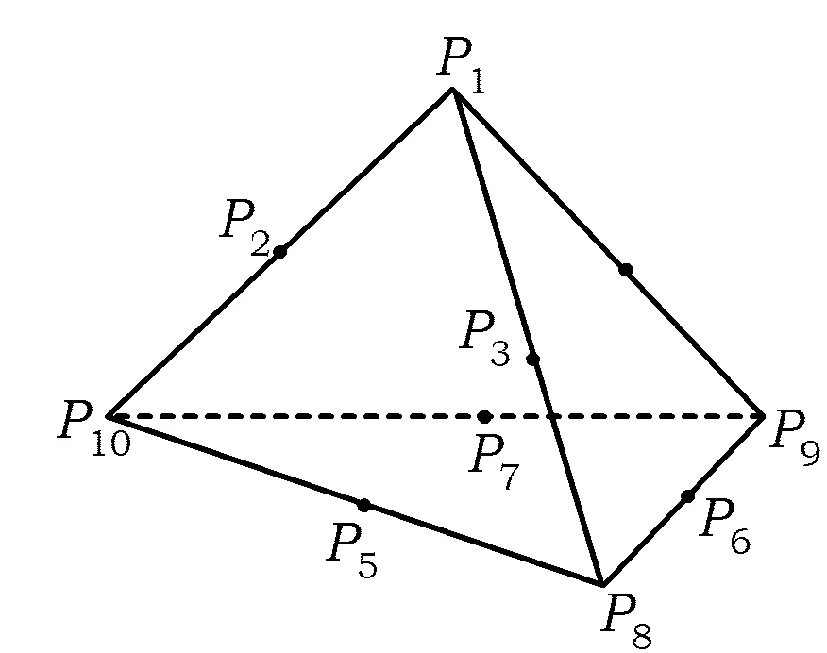
图3
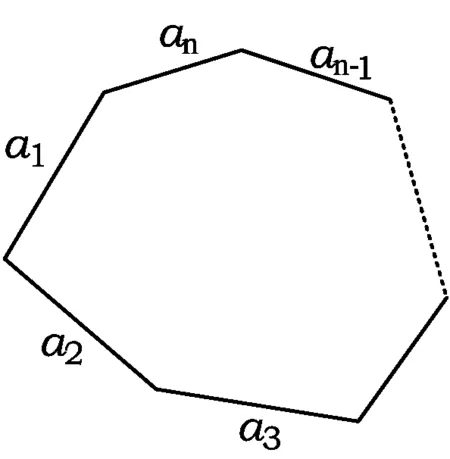
评注 事实上本题是一个环形排列问题,可作如下推广:已知P是n(n≥3)边形内的一点,它与n个点相连构成n个三角形,取k(k≥2)种颜色对这n个三角形涂色,要求相邻2个三角形所涂颜色不同,试求涂色的方案有多少种?
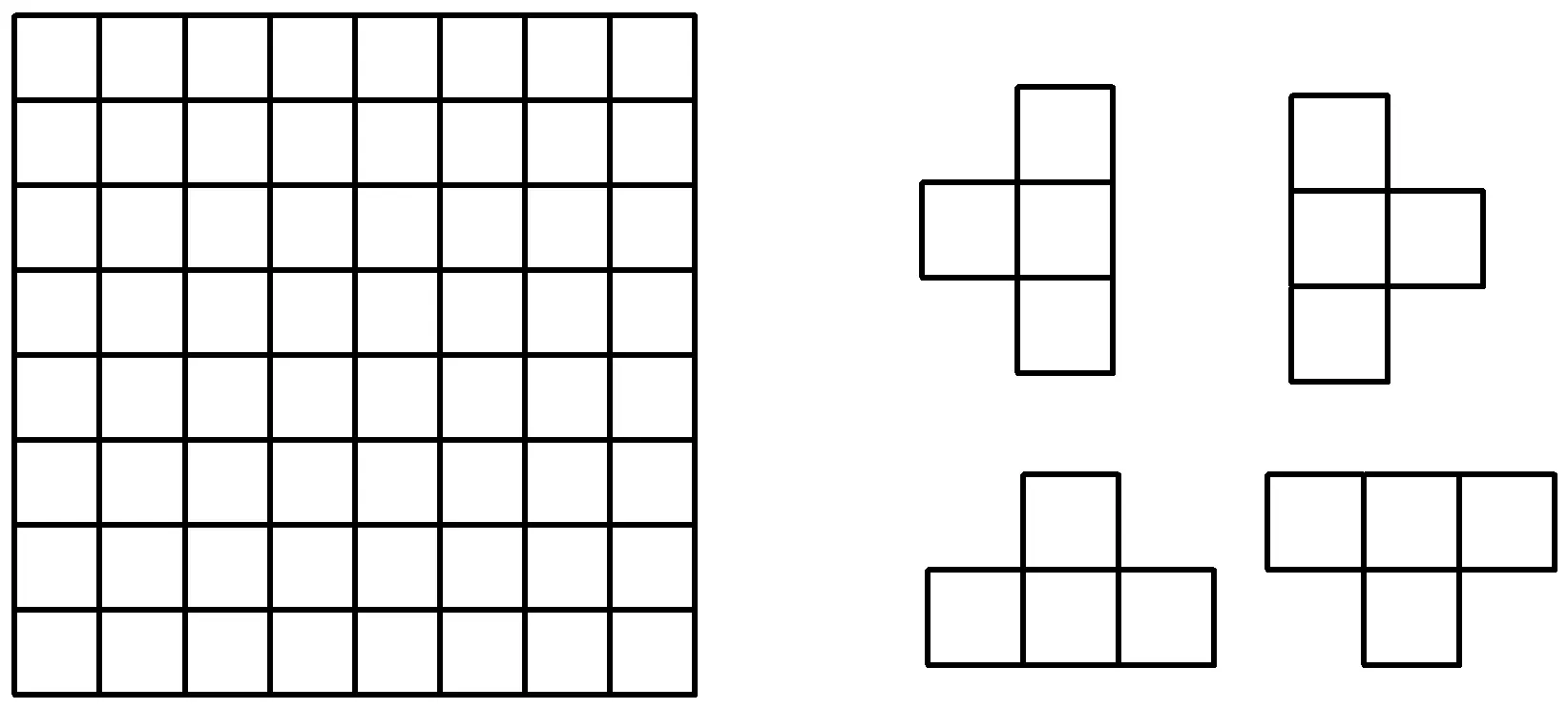
例4 如图3,点P1,P2,…,P10分别是四面体的顶点或棱的中点,那么在同一平面上的四点组(P1,Pi,Pj,Pk) (1 (2002年全国高中数学联赛试题) 解 可分为2类情况讨论: (2)含P1的每条棱上三点组添加底面与它异面的那条棱上的中点组成的四点组也在一个平面上,这样的四点组有3个. 著名数学家华罗庚曾说:“善于‘退’,足够地‘退’,‘退’到最原始而不是去重要性的地方,是学好数学的一个诀窍.”对于有些几何计数问题,当正向思维受阻或需迂回曲折方能达到目的时,用间接法往往能开拓新的解题途径,得出简捷甚至奇异的解,效果更甚. 例5 在正2 006边形中,与所有边均不平行的对角线的条数为 ( ) A.2 006 B.1 0032 C.1 0032-1 003 D.1 0032-1 002 (2006年全国高中数学联赛浙江省初赛试题) 例6 平面上有5个点,任意两点之间用线段连接,这些线段互不平行,互不垂直,也不重合,过其中每个点,都向其他4个点间的线段作垂线,所有这些垂线的交点至多有多少个? (第6届IMO试题) 综上所述,这些垂线的交点至多有435-30-20-75=310个.4 特殊问题一般化 在数学学习过程中,我们经常会将一个数学问题特殊化,从而得到需要的结果,提高解题的效率.但有时也可将一个特殊问题进行一般化地研究,让待解决的问题置于更为一般情形之中,揭示其问题本质,从而解决这一特殊问题或类似问题.对于有些计数问题,我们利用这种“特殊问题一般化”的思考方法,其结果会让人有种“柳暗花明又一村”的感觉. 例7 用5种不同的颜色给图4中“五角星”的5个顶点染色(每个点染一种颜色,有的颜色也可以不用),使每条线段上的2个顶点皆不同色,则不同的染色方法有种______. (2005年全国高中数学联赛江西省初赛试题) 图4 解 将其转化为:具有5个扇形格的圆盘染5种颜色,使得邻格不同色的染色问题.设有k个扇形格的圆盘染5种颜色的方法数为xk,则 xk+xk-1=5·4k-1, 于是x5= (x5+x4)-(x4+x3)+(x3+x2)-x2= 5(44-43+42-4)=1 020. 因此,不同的染色方法有1 020种. 图5 例8 对一个边长互不相等的凸n(n≥3)边形的边染色,每条边可以染红、黄、蓝3种颜色中的一种,但是不允许相邻的边有相同的颜色.问:共有多少种不同的染色方法? (2006年全国高中数学联赛 上海市初赛试题) 解 设不同的染色法有pn种.易知p3=6.当n≥4时,如图5,对于边a1,有3种不同的染法,因为边a2的颜色与边a1的颜色不同,所以对边a2有2种不同的染法,类似地,对边a3,…,边an-1均有2种染法.对于边an,用与边an-1不同的2种色染色,但是,这样也包括了它与边a1颜色相同的情况,而边a1与边an颜色相同的不同染色方法数就是凸n-1边形的不同染色方法数的种数pn-1.因此 pn=3×2n-1-pn-1, pn-2n=-(pn-1-2n-1), 于是pn-2n=(-1)n-3(p3-23)=(-1)n-2·2, pn=2n+(-1)n·2 (n≥3). 综上所述,不同的染色方法数为 pn=2n+(-1)·2. 利用对应(或映射)来解决计数问题,就是通过建立集合A与另一集合B之间的对应(或映射),把对集合A的计数转化为对集合B的计数.实现这种转化的关键是:(1)选择适当的便于计数的集合;(2)建立集合间的对应(或映射)关系. 例9 设有一个凸n边形,不相邻的2个顶点的连线叫做它的对角线.假设没有3条对角线交于凸n边形内部一点,求这些对角线两两相交(在凸n边形内部)的交点总数. (1955年普特南数学奥林匹克竞赛试题) 评注 本题的结论是几何计数中一个重要的结论,可用它解决一些较复杂的几何计数问题. 图6 例10 如图6,在8×8的棋盘上取出一个由4个小方格组成的凸字形,问共有多少种不同的取法? 解 把凸字形上面的那个小方格称为它的头,则每个凸字形恰好有一个头,按凸字形的头在棋盘的边框或内部,把凸字形分为2类: (1)当凸字形的头在棋盘的边框时,则除盘上4个角外,边框上其余的每个方格都唯一地对应着凸字形的一种取法,共有4×6=24种取法; (2)当凸字形的头在棋盘内部时,则棋盘内部的每个方格都对应着凸字形的4种取法,而棋盘内部有6×6=36个方格,因此凸字形共有4×36=144种取法. 由分类计数原理知,共有24+144=168种不同的取法. 例11 设O是边长为1的方格纸上的一个固定的结点.现以Pk表示方格纸上的以点O为起点、长度为k且各段都位于网格线上的所有不同折线的条数,求证:对所有k,都有Pk<2×3k. (第22届莫斯科数学奥林匹克竞赛试题) 证明 (用数学归纳法) (1)当k=1时,有P1≤4<2×3成立; (2)假设当k=m时,结论成立,则当k=m+1时,对于任何一条长度为m+1的满足要求的折线,去掉其最后长度为1的部分,就得到一条长度为m且满足要求的折线.在这个对应过程中,至多有3条长为m+1的折线对应于同一条长度为m的折线,因此 Pm+1≤3Pm<3×2×3m=2×3m-1, 即当k=m+1时,结论也成立. 由(1),(2)可知结论对任何k∈N*都成立. 例12 圆上有n个点(n>1),联结这n个点,依次记为P1,P2,…,Pn,使得折线P1P2…Pn不相交,问这样的联结方法有多少种? 解 先用数学归纳法证明:在点Pn确定的情况下,可联结的方法数有2n-2(n≥2)种: (1)当n=2时,联结P1P2只有1种方法,即1=22-2成立; (2)假设当n=k(k≥2,k∈N)时,有2k-2种联结方法,则当n=k+1时,由于对每一种联结Pk+1的方法,Pk+1必须在P1和Pk之间,因此,连成的折线或是P1P2…PkPk+1,或是Pk+1P1P2…Pk,即有2种可能的选择.由此可得,k+1个点有2×2k-2=2(k+1)-2种联法,即当n=k+1时结论也成立. 由(1),(2)可得在点Pn确定的情况下,可联结的方法数有2n-2(n≥2)种.另外,注意到点Pn的选择有n种,因此,符合题意的联结方法数为n·2n-2种. 计数问题是数学中重要研究对象之一,通过对计数方法的学习和应用,既可以让学生掌握相关的数学内容,处理一些计数问题,又可以培养学生的数学意识,提升数学思想.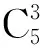
3 考虑间接方法
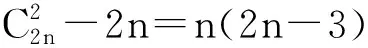
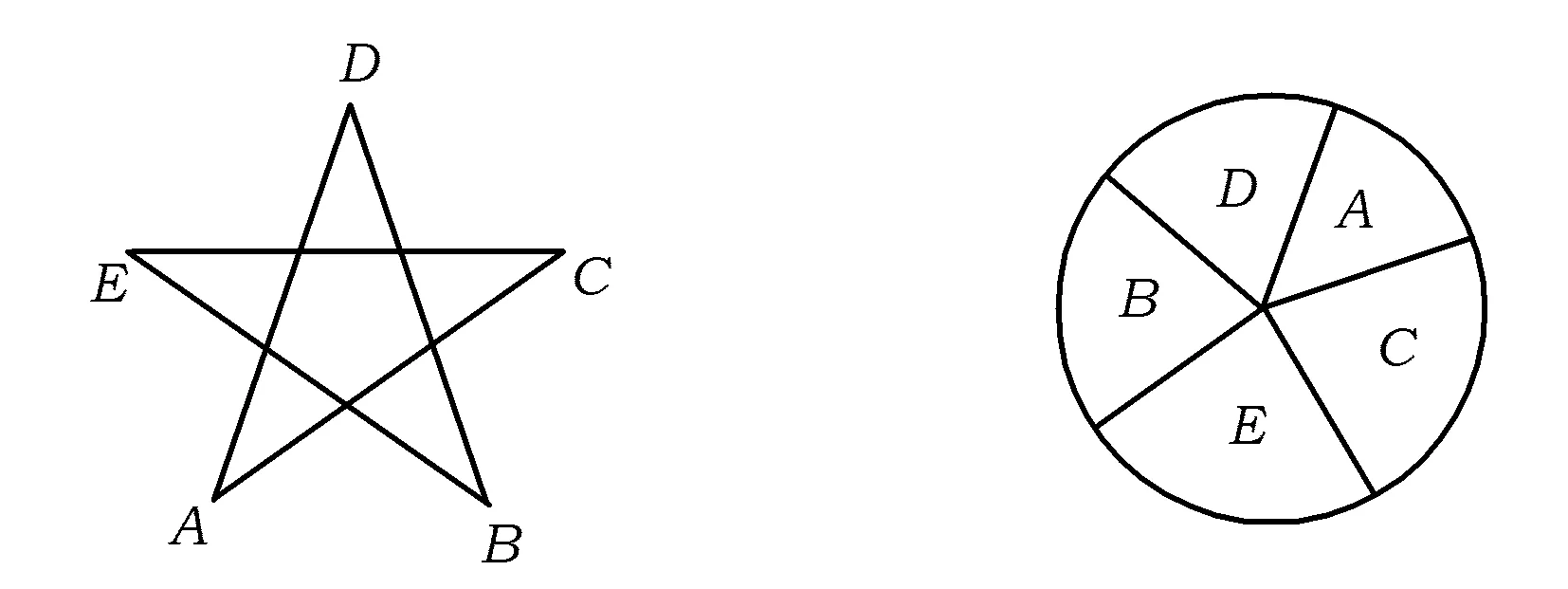
5 构造一一对应
6 用数学归纳法

