直觉对偶犹豫模糊集的集结算子及其应用

吴婉莹，何迎东，郭 甦，陈华友，周礼刚

(安徽大学数学科学学院，安徽合肥230601)

直觉对偶犹豫模糊集建立在直觉模糊集［1－2］与对偶犹豫模糊集［3］的基础上，用一个实数对构成的集合表示隶属度与非隶属度。将直觉对偶犹豫模糊集运用到决策过程中是非常实用的，可以更加具体地描述模糊性的本质，对事物属性的描述提供了更多的方式，使得在处理不确定信息时具有更强的表现能力。

多属性群决策［4－5］广泛存在于社会、经济和管理等领域，其实质就是利用已有的决策信息，通过一定的方式对一组备选方案进行排序或择优。模糊多属性决策已成为当前国内外研究的一个热点。

笔者首先提出直觉对偶犹豫模糊集的概念，并在直觉对偶犹豫模糊集定义的基础上构造其基本运算，接着给出直觉对偶犹豫模糊集的加权平均集结算子［6－9］，最后，将直觉对偶犹豫模糊集的加权平均集结算子应用到多属性群决策中，给出多属性群决策方法，并通过实例说明该方法的可行性和有效性。

1 模糊集定义及运算

定义1 令X是一个固定的集合，X上的直觉模糊集A定义如下:

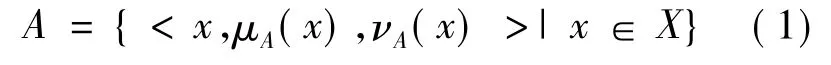
式中，μA(x):X→［0，1］和 νA(x):X→［0，1］分别为A的隶属函数和非隶属函数，且对任意的x∈X，0≤μA(x)+νA(x)≤1。对于 X 中的每个直觉模糊集，称πA(x)=1－μA(x)－νA(x)为x在A中的犹豫度，表示x对A的犹豫程度。显然，对于任意的 x∈X，有0≤πA(x)≤1。

定义2［10－11］令 X为一个给定的集合。形如A={＜x，hA(x)＞|x∈X}的二元组称为X上的犹豫模糊集(HFS)。其中，hA(x)为由区间［0，1］上若干个不同的数构成的集合，表示元素x属于A的若干种可能隶属度构成的集合。为了书写方便，记hA(x)为犹豫模糊元(HFE)。

定义3 令X是一个固定的集合，在X上的对偶犹豫模糊集H定义为:

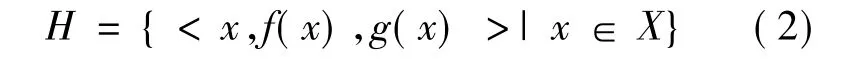
其中，f(x)和 g(x)是两个集合，f(x)⊂［0，1］，g(x)⊂［0，1］，f(x)为 x∈H 的可能隶属度，g(x)为x∈H的可能非隶属度。为方便起见，称H(x)=(f(x)，g(x))为对偶犹豫模糊元，简记为H=(f，g)。

定义4 令X为一个给定的集合，在X上的直觉对偶犹豫模糊集A定义为:

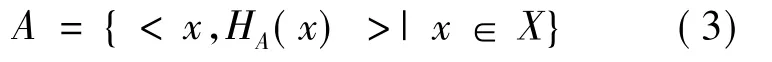
其中，HA(x)为由若干个不同的实数对(fA(x)，gA(x))组成的集合，fA(x):X→［0，1］为A的隶属函数，gA(x):X→［0，1］为A的非隶属函数，且对任意的x∈X，0≤fA(x)+gA(x)≤1。为方便起见，称h=HA(x)是一个直觉对偶犹豫模糊元。

定义5 设X上的直觉对偶犹豫模糊集A={＜x，HA(x) ＞ |x∈X}，犹豫度 πA(x)为由区间［0，1］上若干个不同的数构成的集合，πA(x)=1－fA(x)－gA(x)。显然，对于任意的 x∈X，有0≤πA(x)≤1。

定义6 设A、A1、A2是论域X上的3个直觉对偶犹豫模糊集，则直觉对偶犹豫模糊集的基本运算法则如下:

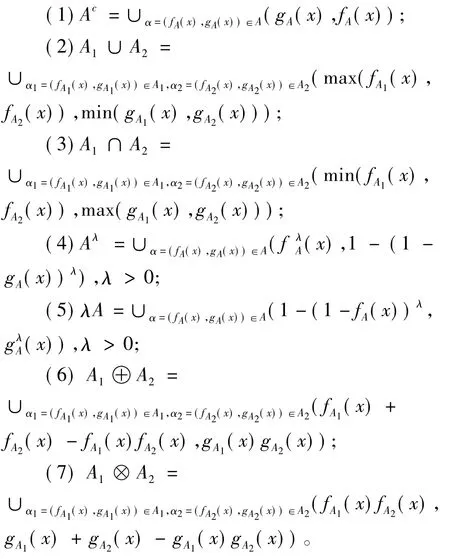
为了比较两个直觉对偶犹豫模糊元的大小，引入直觉对偶犹豫模糊元的得分函数。

定义7 设X上的直觉对偶犹豫模糊元h=HA(x)， 其得分函数定义为，其中#h为 h 中的元素个数。对于两个直觉对偶犹豫模糊元h1和h2，若s(h1) ＞ s(h2)，则h1＞ h2;若s(h1) =s(h2)，则 h1=h2。

2 直觉对偶犹豫模糊集的集结算子

XU和YAGER曾给出了直觉模糊集的有序加权平均算子(OWA)，有序加权几何平均算子，有序加权调和平均算子，以及广义的有序加权平均算子。在这些理论基础上，这里给出直觉对偶犹豫模糊集的一些集结算子。

定义8 设hi(i=1，2，…，n)是论域 X上的一组直觉对偶犹豫模糊元，直觉对偶犹豫模糊集的一些集结算子如下:

(1)直觉对偶犹豫模糊算术加权平均算子:

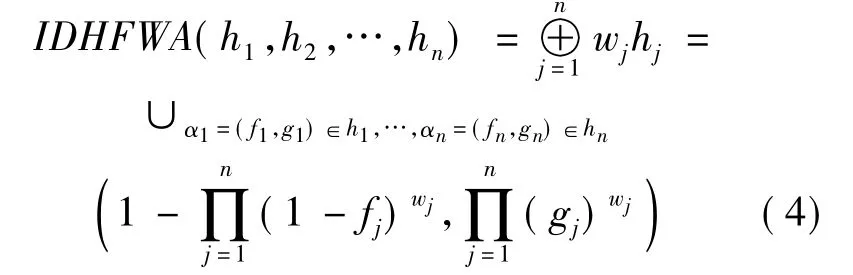
(2)直觉对偶犹豫模糊有序加权算术平均算子:

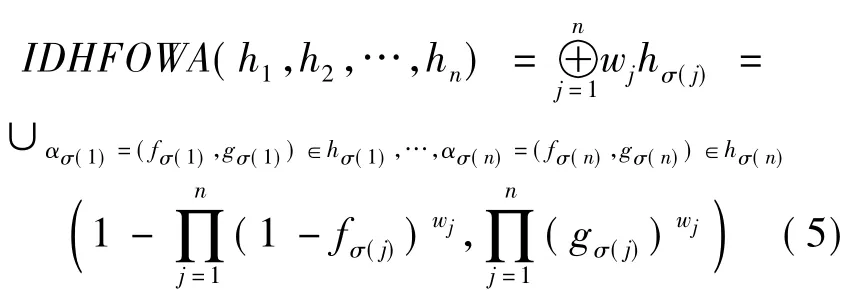
(3)广义的直觉对偶犹豫模糊有序加权算术平均算子:

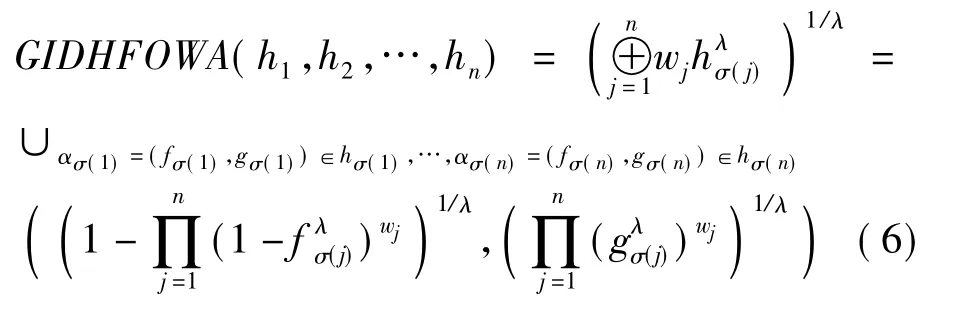
(4)直觉对偶犹豫模糊加权几何平均算子:

(5)直觉对偶犹豫模糊有序加权几何平均算子:

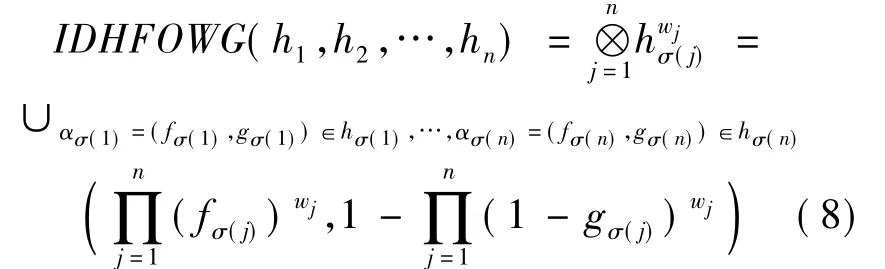
(6)广义直觉对偶犹豫模糊有序加权几何平均算子:

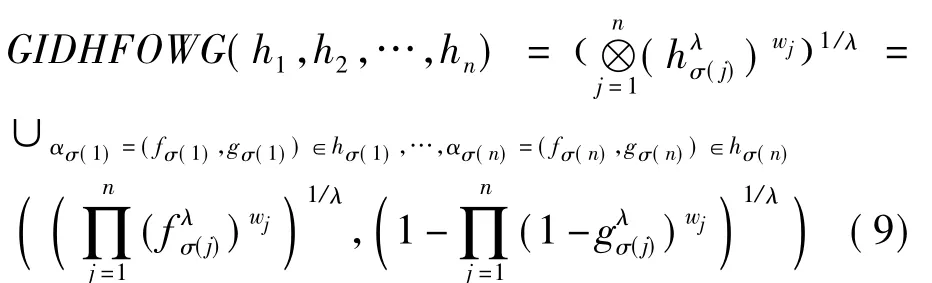
式中:hσ(j)为 hi(i=1，2，…，n) 中第 j大的数;λ ＞ 0;w=(w1，w2，…，wn)T为 h1，h2，…，hn的权重向量，满足 wj∈［0，1］，j=1，2，…，n，且

定理1 直觉对偶犹豫模糊加权几何平均算子具有以下性质:

(2)幂等性。设(h1，h2，…，hn)为直觉对偶犹豫模糊元，若对任意的 i，有hi=h，则IDHFWG(h1，h2，…，hn)=h。

(3)介值性。直觉对偶犹豫模糊加权几何平均算子介于 max算子与 min算子之间，即min(hi)≤IDHFWG(h1，h2，…，hn)≤max(hi)。其中max(hi)={max fi，min gi} ，min(hi)={min fi，max gi}。

(4)若 w=(1/n，1/n，…，1/n)T，则相应的直觉对偶犹豫模糊加权几何平均算子即为几何平均算子:

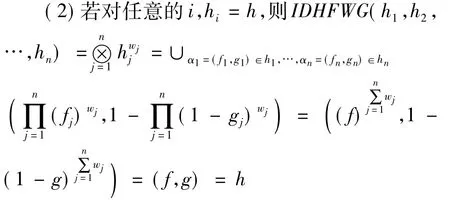
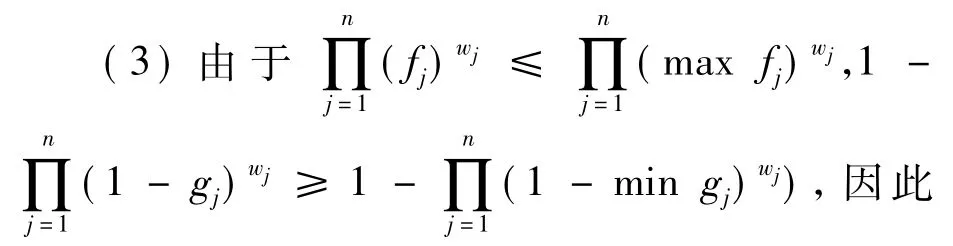
(4)将权重 w=(1/n，1/n，…，1/n)T代入直觉对偶犹豫模糊加权几何平均算子的计算公式即可。

3 直觉对偶犹豫模糊集的多属性群决策

在实际问题中，为了保护决策者的隐私以及避免相互影响，往往采取匿名的形式，如总统选举或论文盲审。这里，将直觉对偶犹豫模糊集的集结算子应用于匿名的多属性群决策中［12］。假设Yi(i=1，2，…，m) 为方案集，Gj(j=1，2，…，n)为属性集，权重向量为 w=(w1，w2，…，wn)T。决策者采取匿名的形式对方案Yi在属性Gj给出评价值，且评价值以直觉对偶犹豫模糊元hij的形式给出。通过1个实例说明具体的决策方法。

例如银行打算贷款给公司进行运作，在对市场进行考察后，有3家公司在考虑范围内:①制药公司Y1;②食品公司Y2;③家具公司Y3。在进行对比时，主要考虑以下3个方面:①短期收益G1;②长期收益G2;③投资风险G3。专家组由3名成员组成，每位成员均采取直觉对偶犹豫模糊元的形式表达自己的观点。结果如表1所示，属性的权重向量 w=(0.33，0.41，0.26)T。

(1)为了避免相互影响，决策者采取匿名的方式给出评价值，决策矩阵H=(hij)m×n如表1所示，hij均为直觉对偶犹豫模糊元的形式，表示方案Yi在属性Gj下的评价值。

(2)使用GIDHFOWA算子和GIDHFOWG算子对方案Yi的属性值进行集结，取λ=2，得到相应的直觉对偶犹豫模糊元hi(i=1，2，…，m)。

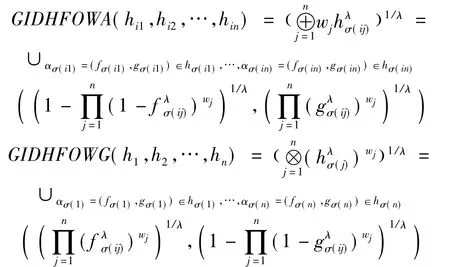
(3)计算得分函数s(Yi)的值，GIDHFOWA算子 的结果为:s(Y1)=0.7876，s(Y2)=0.8554，ns(Y3)=0.833 6;GIDHFOWG 算子的结 果 为:s(Y1)=0.656 8，s(Y2)=0.847 8，s(Y3)=0.798 5。

表1 决策矩阵

(4)将s(Yi)的值按照降序进行排列s(Y2)＞s(Y3)＞s(Y1)，则得到最优方案为投资食品公司是Y2。在直觉模糊集环境下，根据集结算子和得分函数的运算，得到最优方案也是Y2。

4 结论

笔者给出了直觉对偶犹豫模糊集的定义，构造了其基本运算，提出了直觉对偶犹豫模糊集的信息集结算子，并将其应用于解决多属性群决策问题，通过一个实例说明该方法的实用性和可行性。

［1］ATANASSOV K T.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986(1):87 －96.

［2］ATANASSOV K T.New operations defined over the intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1994(2):137－142.

［3］ZHU B，XU Z，XIAM.Dualhesitant fuzzy sets［J］.Journal of Applied Mathematics，2012，32(5):317 －386.

［4］LID F.Multi－ attribute decision making models and methods using intuitionistic fuzzy sets［J］.Journal of Computer and System Sciences，2005，70(1):73 －85.

［5］XU Z.Intuitionistic preference relations and their application in group decision making［J］.Information Sciences，2007，177(11):2363 －2379.

［6］XU Z.Intuitionistic fuzzy aggregation operators［J］.IEEE Transactions on Fuzzy Systems，2007，15(6):1179－1187.

［7］XIA M，XU Z.Hesitant fuzzy information aggregation in decision making［J］.International Journal of Approximate Reasoning，2011，52(3):395 －407.

［8］YAGER R R.On ordered weighted averaging aggregation operators in multicriteria decision making［J］.IEEE Transactions on Systems，Man and Cybernetics，1988，18(1):183 －190.

［9］XU Z，YAGER R R.Some geometric aggregation operators based on intuitionistic fuzzy sets［J］.International Journal of General Systems，2006，35(4):417 －433.

［10］TORRA V.Hesitant fuzzy sets［J］.International Journal of Intelligent Systems，2010，25(6):529 －539.

［11］TORRA V，NARUKAWA Y.On hesitant fuzzy sets and decision［C］∥IEEE International Conference on Fuzzy Systems.［S.l.］:［s.n，］，2009:1378 －1382.

［12］邱方鹏，莫莉.基于直觉模糊集的产品规划评估群决策研究［J］.武汉理工大学学报:信息与管理工程版，2013，35(5):723 －727.