衰落信道下的传感器网络局部容错目标检测

刘守军，刘克中，陈 伟

(1.武汉理工大学 信息工程学院，湖北武汉430070;2.武汉理工大学 航运学院，湖北武汉430063)

无线传感器网络由众多传感器节点组成，节点之间相互协作，自组织形成多跳网络，能广泛应用于环境监测和目标跟踪等领域。传感器节点往往通过人工投放或者飞机播撒，部署在野外无人区域，环境较为恶劣，节点容易遭受破坏，出现故障。此外，传感器节点由电池供电，能量十分有限，容易因能量耗尽而停止工作。因此，单个传感器节点的工作状态并不可靠，容易出现故障。为了提高系统检测性能，可以利用数据融合技术对众多传感器节点的判决进行融合处理，结合相邻节点观测数据之间的空间相关性，消除错误判决，从而增强网络容错能力。文献［1］提出了分布式贝叶斯检测算法，通过邻居节点交互信息实现容错和事件检测。文献［2］将计数规则应用于分布式目标检测，该方法虽较为简单，但没有充分利用节点间的协作性。文献［3］提出了应用于目标检测的局部投票决策融合算法，并取得了良好的检测效果。在此基础上，文献［4］提出了近似计算系统判决阈值的改进方法。上述文献均为假设理想信道的情况，没有考虑衰落信道的影响。文献［5－6］针对衰减信道提出了次优的决策融合规则，在系统性能、算法复杂度、占用系统资源大小之间进行折衷，但其假设是本地判决已经形成，并且没有考虑节点之间的差异。笔者在上述文献的基础上，考虑了衰落信道并且存在节点故障情况下的目标检测问题，提出了一种基于邻居节点观测数据的局部容错决策融合算法。仿真结果表明，该算法具有良好的检测性能。

1 问题描述与检测模型

笔者以无线传感器网络监控车辆为应用场景，利用车辆行驶时产生的声音、振动和红外辐射等信号，对监控区域内出现的车辆目标进行检测［7］。为了简化分析，只考虑单个信号即声音强度的检测问题。

1.1 系统模型

笔者采用并行结构分布式检测系统，如图1所示，假设系统中有N个传感器节点，所观测的目标为H，H1为目标出现，H0为目标未出现。传感器节点首先基于检测到的声音信号对目标是否出现作出初步判决 u1，u2，…，uN，ui∈{0，1}，i=1，2，…，N;然后在邻域内对判决结果进行容错处理，各个节点根据处理结果修正初步判决，得到局部判决x1，x2，…，xN;为了减少信息传输，达到降低系统能耗的目的，传感器仅在局部判决xi=1时，将局部判决结果通过无线信道上传到融合中心，融合中心再对接收信号yi，y2，…，yN进行融合处理，最后作出全局判决u0，从而判断目标是否出现。

1.2 信号模型

单个传感器节点i首先对混有噪声的声音信号进行检测，相应的观测值Si分别为:

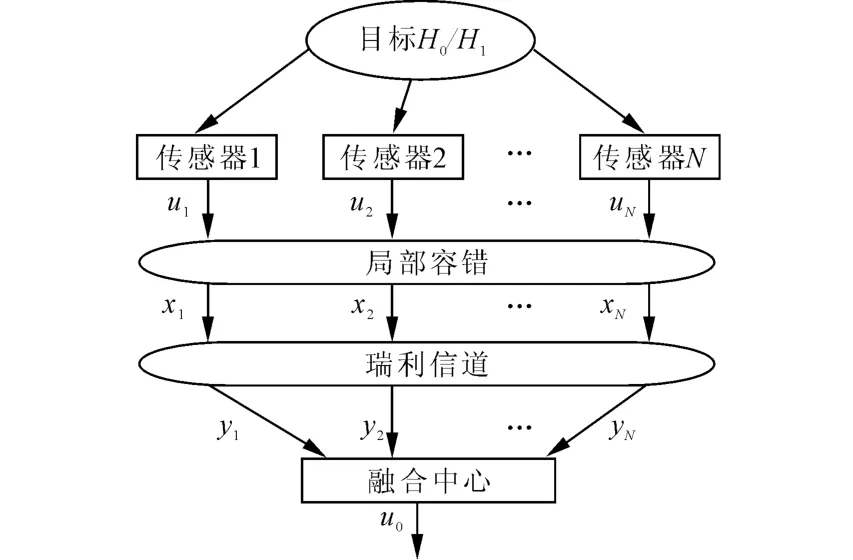
图1 基于衰落信道的并行结构分布式检测系统

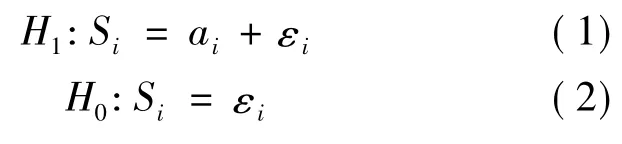
式中:εi为零均值且方差为σ2n的高斯噪声;ai为节点处的信号幅度，大小取决于信号衰减模型。笔者采用以下信号衰减模型［8］:

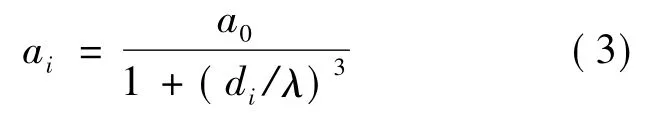
式中:a0为检测对象发射的信号幅度;di为节点到检测对象的欧氏距离;λ为信号衰减常数;信噪比 SNRn=20lg(a0/σn)。

1.3 信道衰落模型

假设无线信道服从瑞利衰落，融合中心接收到的信号yi为:

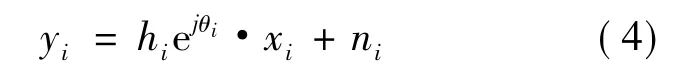
式中:xi为节点的局部判决结果，xi∈{0，1};ni为复高斯噪声，实部和虚部均服从零均值且方差为σ2的高斯分布;hi为瑞利分布的信号包络，其概率密度函数为:

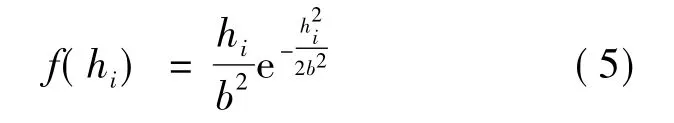
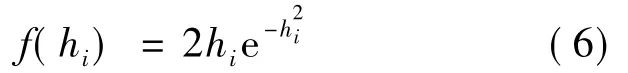
假设信道噪声相互独立，信噪比 SNRc=10lg(1/2σ2)。

2 容错算法及融合规则

2.1 容错算法描述

(1)节点i首先基于观测信号作出初步判决ui，ui∈{0，1}，若观测值大于等于局部判决阈值τ，则判决目标出现，否则判决目标未出现。相应得到节点的虚警概率和检测概率分别为:

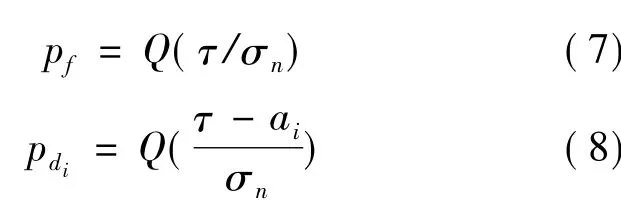
其中:

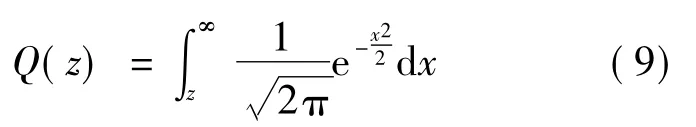
(2)由于节点的工作环境比较恶劣，节点可能遭受破坏，出现故障，从而产生错误判决。考虑两种情形:①目标未出现，而传感器节点因故障误判为目标出现;②实际有目标出现，而传感器节点因故障误判为目标没有出现［9］。假设两类故障的概率分别为p1和p2，且p1=p2=p/2，则考虑传感器故障后的节点虚警概率和检测概率分别为:

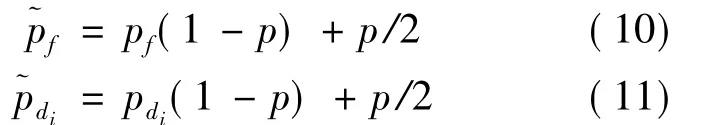
(3)N个节点分别将判决结果发送给各自的邻居节点。

(4)节点i根据邻居节点的判决结果，按照多数原则更新自己的判决，得到局部判决即若有否则，xi=0，其中N(i)为以节点i为中心的邻居节点集合，Mi为N(i)中的节点个数。

2.2 融合规则

考虑到融合中心接收到的信号yi为复信号，直接处理较为困难，因此将接收信号的功率zi作为决策融合统计量。即:

根据贝叶斯准则，使系统平均风险达到最小的似然比判决LR是最优的融合规则［10］。即:

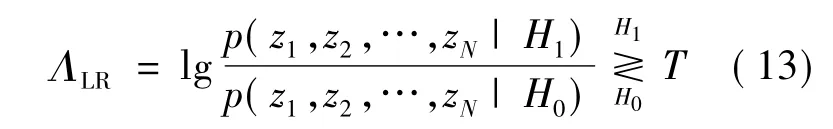
其中，T为系统阈值。

在理论上似然比融合规则是最优的，但是需要知道信道和节点的参数，并且要求各传感器节点的判决相互独立，显然局部容错后的判决并不满足相互独立的条件，因此笔者对最优似然比融合规则进行近似处理，提出次优的简单平均融合规则。该融合规则直接对接收信号功率zi求和，再与系统阈值T作比较，如果大于阈值，则判决目标出现，否则判决目标未出现。即:

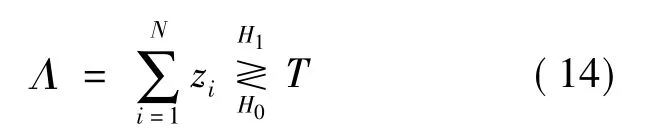
2.3 阈值计算

由于考虑了节点之间的协作，各个传感器节点不再是相互独立的，局部判决结果之间存在着空间相关性。

在目标未出现的情况下(即H0情况)，局部判决xi服从二项式分布，其均值为:

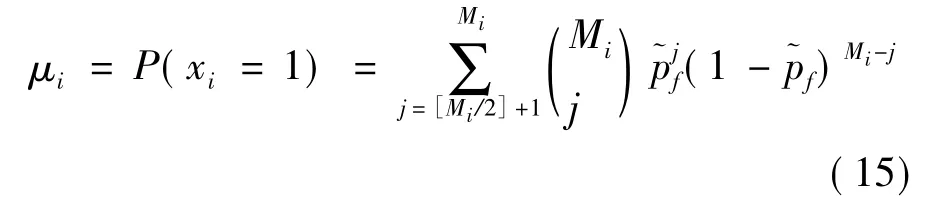
其中，［.］为向下取整。

Λ在H0条件下的均值和方差分别为:

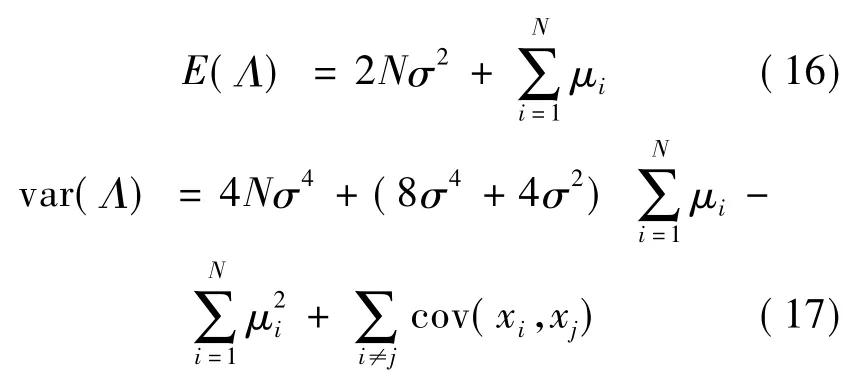
上述均值和方差由附录Ⅰ给出。局部判决协方差cov(xi，xj)的计算公式见参考文献［3］。

对于规则网格分布或随机分布的大量传感器组成的网络，Λ近似服从正态分布，从而系统虚警概率为:

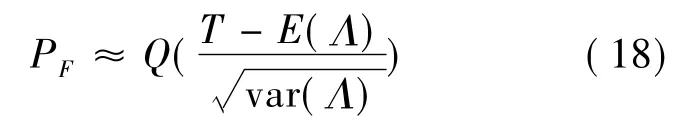
已知系统虚警概率，通过式(19)可近似求得系统阈值T。

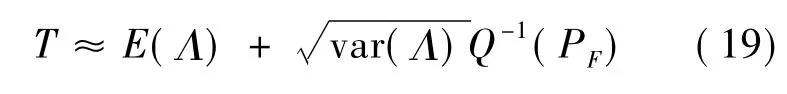
3 实验结果与分析

利用Matlab软件对算法进行仿真实验，假设节点基于正方形网格分布在100 m×100 m的区域内，信号源位于区域中心，目标发射功率P0=1W，信号衰减常数λ=15，邻居节点个数M=5，节点虚警概率 pf=0.1，信噪比 SNRn=10 dB，SNRc=7 dB。为了说明局部容错决策融合算法(LFTDF)的性能，将其与文献［2］提出的能量检测决策融合算法(EDDF)进行了比较。

图2为分别通过蒙特卡罗仿真和数值近似得到的LFTDF算法ROC曲线，可以用来衡量数值近似对系统真实性能的逼近程度。其中，节点个数N=100，节点故障概率p=0.1。由图2可以看出，蒙特卡罗仿真和数值近似的曲线有少量偏差，但在虚警概率较高时两曲线基本吻合，逼近程度良好。

图3为反映系统检测概率与虚警概率关系的ROC曲线，其中节点个数N=100，节点故障概率p=0.2。由图3可以看出，LFTDF算法的检测性能明显优于EDDF算法。例如，当系统虚警概率为0.15时，LFTDF算法和EDDF算法的检测概率分别为 88.32%和 77.3%，相差 11.02%。

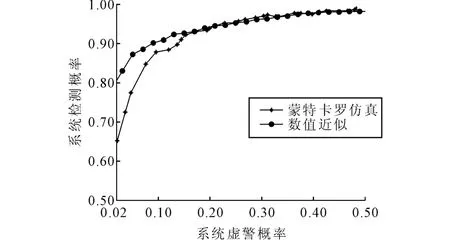
图2 LFTDF算法ROC曲线(蒙特卡罗仿真与数值近似)

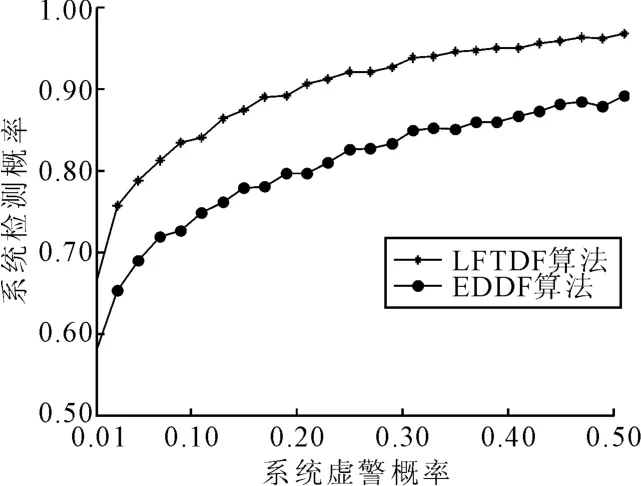
图3 系统ROC曲线

图4 为系统检测概率随节点故障概率变化的关系曲线图，其中节点个数N=100。由图4可以看出，随着节点故障概率的增加，两种算法的检测概率均在下降，但LFTDF算法的系统检测概率较EDDF算法均有较大程度提高。当节点故障概率较低时，LFTDF算法的性能改善程度优于故障概率为0的情况。例如，当节点故障概率为0.2时，系统虚警概率为0.1对应的LFTDF算法的检测概率比EDDF算法提高了11.4%，系统虚警概率为0.2对应的LFTDF算法的检测概率比EDDF算法提高了9.7%;而当节点故障概率为0时，则分别提高了6.37%和4.8% 。这表明该算法对节点故障具有较好的容错能力。当节点故障概率较高时，改善程度明显下降，这是由于可靠节点个数过少的缘故。

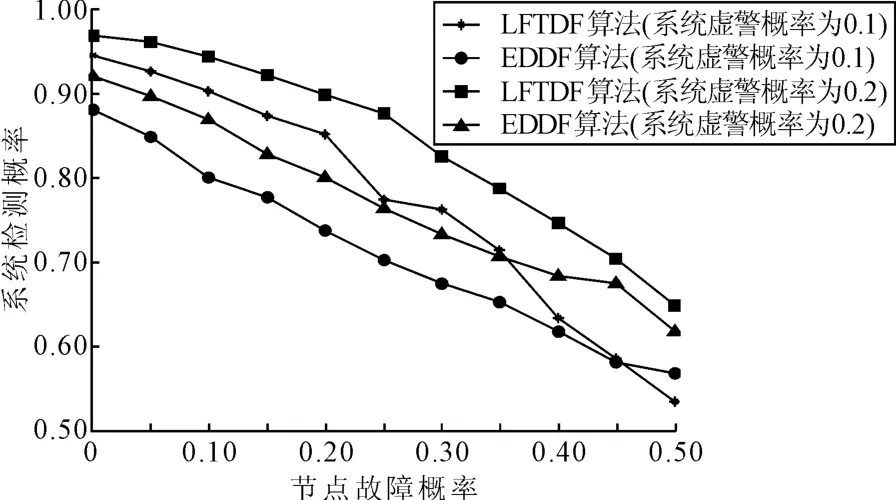
图4 系统检测概率随节点故障概率的变化关系

图5为系统检测概率随节点个数变化的关系曲线图，其中节点故障概率p=0.1，系统虚警概率为0.1。由图5可以看出，随着节点个数的增加，系统的检测概率均在上升。当节点个数过少时，LFTDF算法的检测概率低于EDDF算法;随着节点个数的增加，LFTDF算法的检测概率较EDDF算法有明显提高;当节点个数过多时，两者的检测概率较为接近，改善程度下降。因此，对于中等规模传感器网络，该算法可以显著提高系统检测性能。

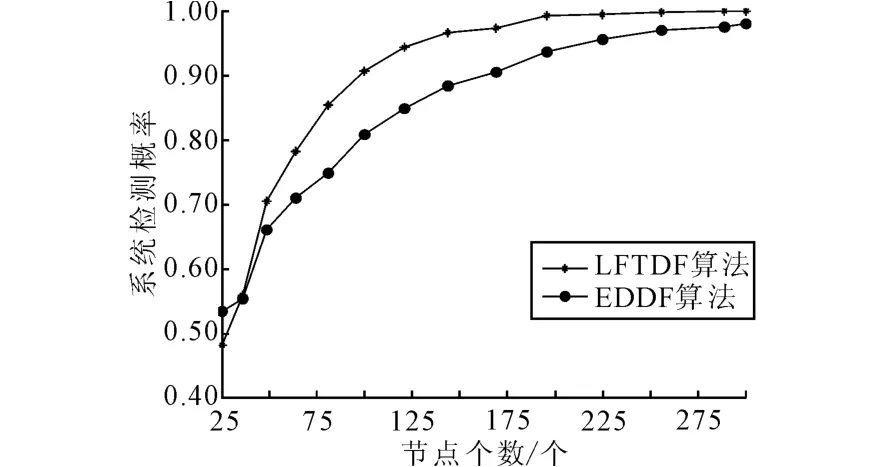
图5 系统检测概率与节点个数的关系

4 结论

针对衰落信道下的目标检测问题，提出了一种基于局部容错机制的决策融合算法。该算法利用邻居节点数据的空间相关性，按照多数原则纠正节点错误，提高了系统的容错能力。对最优似然比融合规则进行近似处理，提出了次优的简单平均融合规则。仿真结果表明，该算法在中等规模的无线传感器网络环境下可以显著提高系统检测概率，容错效果良好。

附录Ⅰ

令nIi、nQi分别为复噪声信号ni的实部和虚部，则Λ在H0条件下的均值为:

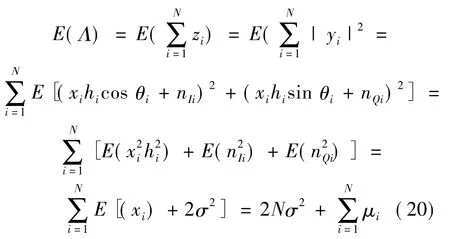
Λ在H0条件下的方差为:

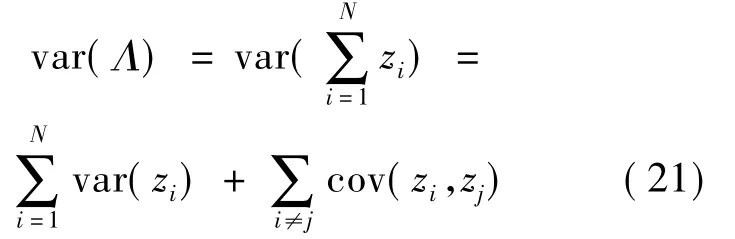
由于:

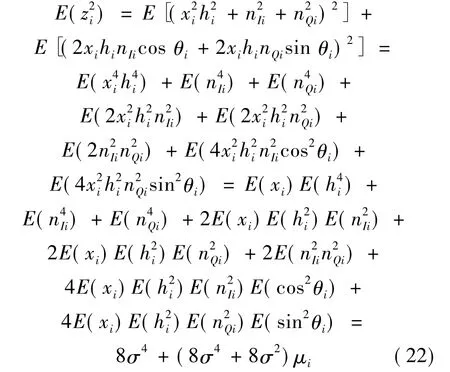
故而:

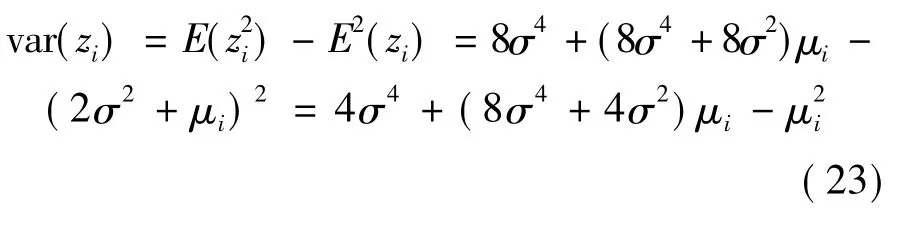
又有:

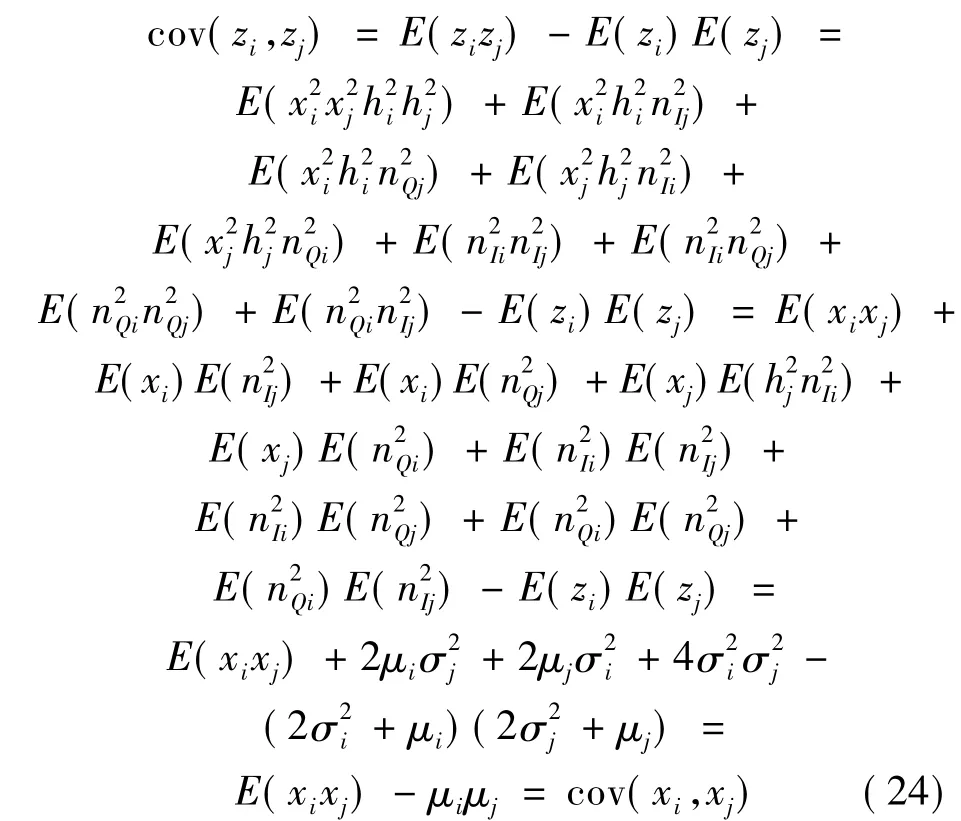
将式(23)和式(24)代入式(21)可得:

［1］KRISHNAMACHARIB，LYENGAR S.Distributed basesian algorithms for fault－tolerant event region detection in wireless sensor networks［J］.IEEE Transactions on Computers，2004，53(3):241 －250.

［2］R UIXIN N，PRAMOD K V.Performance analysis of distributed detection in a random sensor field［J］.IEEE Transactions on Signal Processing，2008，56(1):339－349.

［3］NATALLIA K，ELIZAVETA L，GEORGE M.Local vote decision fusion for target detection in wireless sensor networks［J］.IEEE Transactions on Signal Processing，2008，56(1):329 －338.

［4］MARTIN S R.An improved threshold approximation for local vote decision fusion［J］.IEEE Transactions on Signal Processing，2013，61(5):1104 －1106.

［5］李燕君，王智，孙优贤.资源受限的无线传感器网络基于衰减信道的决策融合［J］.软件学报，2007，18(5):1130－1137.

［6］戎舟，王锁萍.基于衰减信道的无线传感器网络次优决策融合算法［J］.仪器仪表学报，2010，31(11):2622－2628

［7］王声才，李艾华，肖秋生，等.衰落信道WSN网络基于投票机制的决策融合［J］.解放军理工大学学报:自然科学版，2011，11(1):49 －53.

［8］LID K，HUW Y，SAYEED A.Detection，classification，and tracking of targets［J］.IEEE Transactions on Signal Processing，2002，50(2):17 －29.

［9］LUOXW，DONGM，HUANGY L.On distributed fault－ tolerant detection in wireless sensor networks［J］.IEEE Transactions on Computers，2006，55(1):58 －70.

［10］韩崇昭.多源信息融合［M］.北京:清华大学出版社，2006:195－200.