基于改进MSPCA的交通检测器故障诊断模型

张 凯，陆百川，马庆禄，刘权富，邓 捷

(1.重庆交通大学交通运输学院，重庆400074;2.重庆山地城市交通系统与安全实验室，重庆400074)

主元分析(principal component analysis，PCA)经常被应用于过程监控及故障诊断，由于该方法仅限于建立固定的、单尺度模型［1］，在面对噪声的时变性和故障信息的多尺度特性等现状时，检测效果并不理想。因此，为了克服PCA的不足，国内外很多研究者在其基础上发展了不同类型的主元分析模型，BAKSHI提出了多尺度主元分析的故障诊断方法，即MSPCA模型［2］，该模型不依赖目标系统的解析模型，而是从过程数据出发，将小波分析与PCA相结合，使用PCA对离线数据进行多元统计分析，利用小波的多尺度特性克服了常规PCA的缺点，但该模型在实际应用过程中的抗噪能力存在明显缺陷，这是因为MSPCA在处理超出统计控制限的小波系数时，采用该尺度下统一的阈值进行小波重构，而没有考虑噪声的时变性，因此部分噪声会被误认为是故障而被分离，且部分被噪声覆盖的故障也会被扩大范围，出现故障误报现象。文献［3－4］中提出了自适应PCA的方法，该方法能够有效处理数据中的缓变数据，减少由于时变效应以及设备老化而导致的故障诊断漏报。但该方法没有考虑数据的多尺度特性，其抗噪能力欠佳。

笔者在传统MSPCA的基础上加入了一种改进的小波阈值除噪算法，并借鉴自适应PCA处理缓变及突变变量时建立多向主元的方法，设计了一种改进的MSPCA故障诊断模型，将改进的模型应用在线圈检测器的故障诊断中，通过与传统MSPCA模型及自适应PCA模型进行对比，结果证明该模型具有较小的误报率和漏报率，准确率更高，抗噪能力更强。

1 改进的小波阈值除噪

小波阈值除噪的基本思想是预先设置一个临界值λ，该值即为阈值。将小波变换后得到的高频细节系数与该阈值进行比较，若小于该临界值，则认为该系数主要由噪声引起，需要去除;反之则保留。笔者提出的小波阈值除噪方法是在传统软阈值除噪算法［5］的基础上对其中的3个方面进行修改:噪声标准方差估计、阈值设定函数和小波系数调整函数。

(1)噪声标准差估计公式。将信号进行多尺度分析时，每一个尺度都会有一个近似部分系数［6］CAj和一个细节部分系数 CDj。噪声的标准方差可用以下经验公式计算:

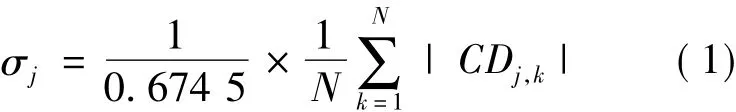
式中:j为尺度数，且1≤j≤J，J为最大尺度;N为该尺度下小波系数的个数。

(2)阈值设定函数。已知DONOHO给出的统一阈值公式:将第 j 层小波系数的绝对值从小到大进行排列，得到一个向量P=［CDj，1，CDj，2，…，CDj，N］，使得 CDj，1≤CDj，2≤CDj，3≤…≤CDj，N。由此计算第 j层小波系数下的风险向量其中:

对风险向量中的各值进行排序，获得最小值，以该值为逼近误差，相对应地找出CDmin，因此有第j层小波系数的自适应阈值为

计算第j层小波系数绝对值的平均值Pa，j，及极小能量水平ρN，j。故阈值选择函数为:

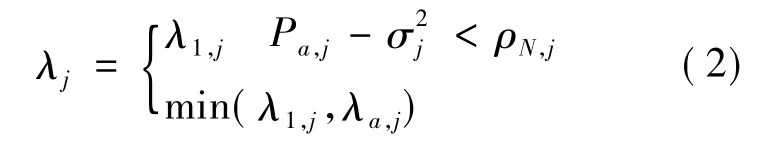
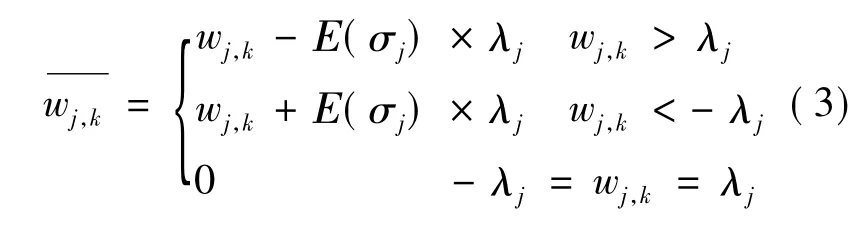
2 改进的MSPCA故障诊断模型

2.1 故障诊断原理

基于PCA的故障诊断思想是利用海量历史正常数据来建立主元子空间和残差子空间，将待检数据投影到该空间内［7］，再利用某参数描述某数据在主元空间中“正确程度”或某数据在残差空间的“错误程度”。

文献［8］提出采用T2这个指标来描述故障是否发生，该指标反映了每个数据采样点的幅值或变化趋势相对于其主元子空间原点的距离。文献［9］介绍了使用SPE指标来确定故障，该统计量用来反映k时刻的观察数据x(k)相对于其主元模型的背离程度。

2.2 模型改进方法及流程图

在实际交通检测器故障监控过程中发现，早晚高峰时交通流会剧烈变动，因此笔者提出的模型改进思想是对交通流进行分段处理，灵活调整主元和其对应的控制限参数。另外，在算法中加入所设计的小波阈值除噪算法，将样本数据的每一列进行小波分解，将各分量中的噪声进行滤除，再进行PCA。故障诊断模型流程如图1所示。

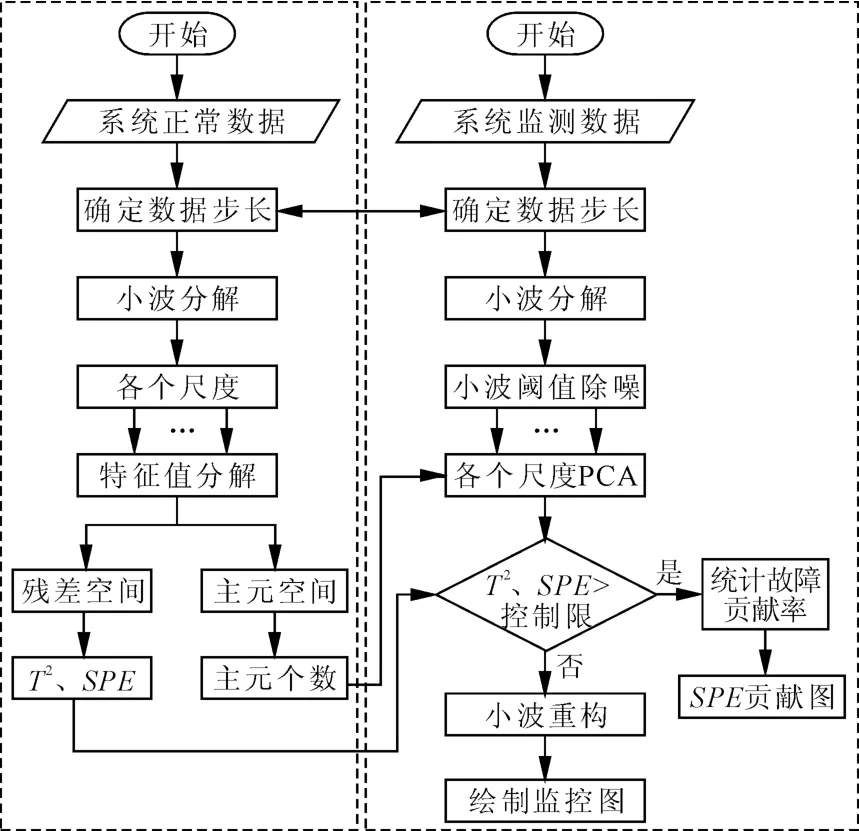
图1 故障诊断模型流程图

3 仿真实验及结果分析

3.1 实验数据的采集

选取重庆某交叉口线圈检测器数据作为实验数据来源。该交叉口每个车道停车线前有一个线圈，共10个线圈。每个检测器一天约产生555个数据，即每天数据量大小为5 550个。图2是某工作日检测得到的数据，其中在线圈6和线圈7中，数据点281～298和315～326之间有故障发生。在所有数据上添加高频随机白噪声后，以该数据作为含故障和噪声的待检数据。

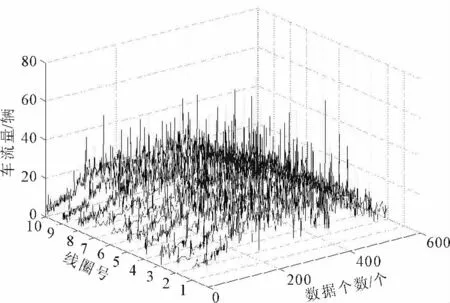
图2 线圈检测器待检数据展开图

3.2 误差指标定义

定义误报率μf、漏报率μg以及故障算法准确率Φ［10］。误报率表示某数据不是故障，但错报成故障的情况，漏报率表示某数据本应是故障，却没有被检测到的情况。

计算方法如下:μf=n/N，μg=m/N。n为误报数据点个数，m为漏报点个数，N为数据总个数。准确率和 δ2SPE分别为使用T2和SPE时进行故障诊断的准确率，其中:

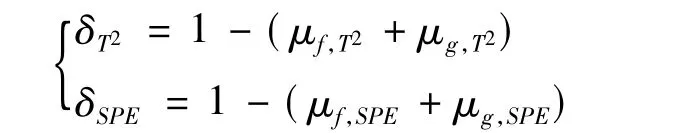
3.3 参数设置

Matlab仿真中，两种模型的小波分解均采用DB3小波［11］。计算T2统计量和SPE统计量参数的时候选取置信度为99%。主元累计贡献率不小于85%。

3.4 实验结果及分析

3.4.1 传统MSPCA实验

MSPCA模型是基于离线数据的计算方法，因此，在使用历史正常数据对某模型进行预处理后，将一天的待检数据输入，得到SPE监控图与T2监控图，对明显故障位置计算二维贡献图。结果如图3所示。

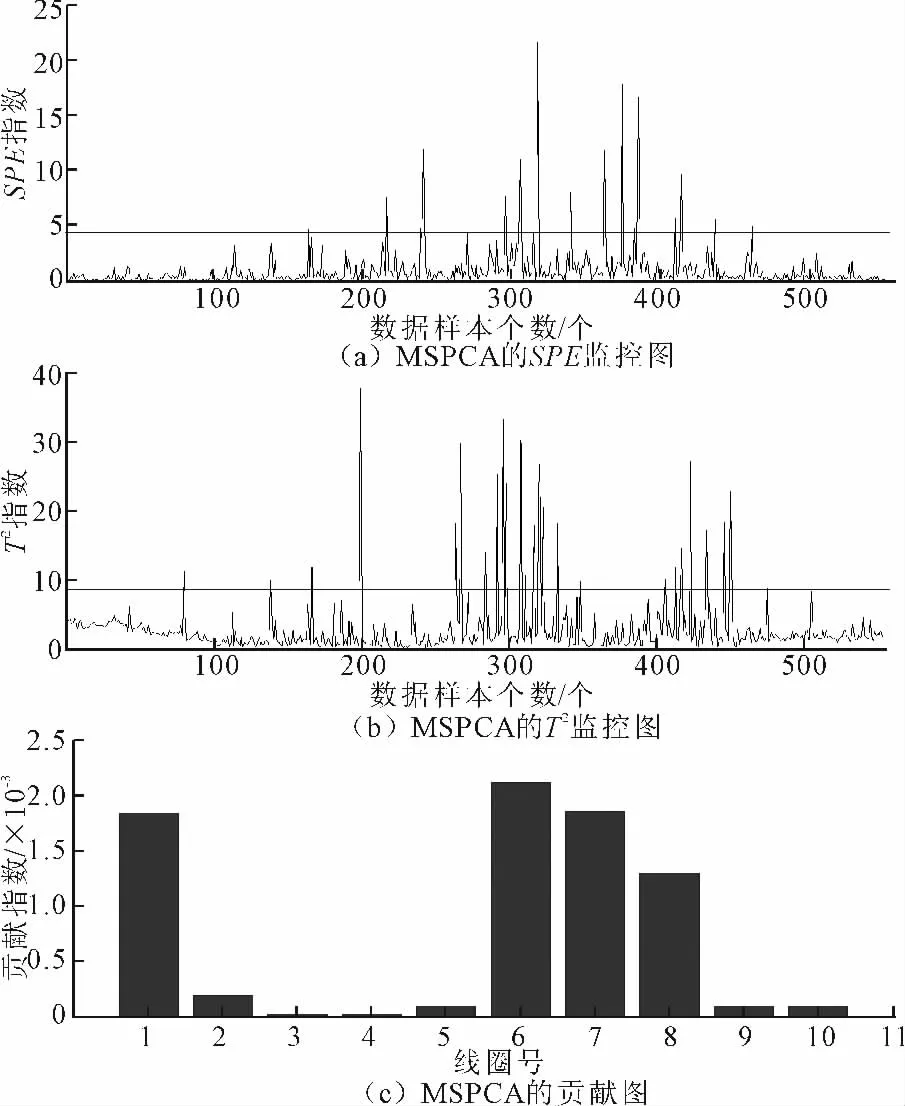
图3 MSPCA实验结果图

3.4.2 自适应PCA实验

采用相同实验数据，在利用历史正常数据对模型进行预处理后，完成对监测数据的多向主元建模，再模拟在线数据的输入，最终得到两个监控图和故障定位的贡献图，结果如图4所示。

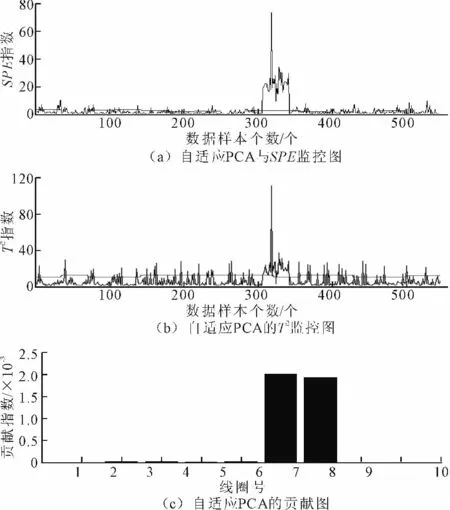
图4 自适应PCA实验结果图

3.4.3 改进MSPCA实验

使用相同历史数据完成模型的预处理后，逐渐输入待检数据来模拟在线数据。发现明显故障位置后进行贡献率计算，最终结果如图5所示。

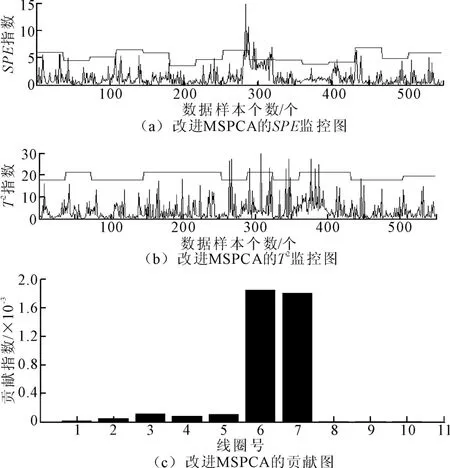
图5 改进MSPCA实验结果图

对比3个模型的实验结果可发现，由于噪声的干扰，传统MSPCA将很多噪声误认为故障，导致误报情况，而在计算传感器故障贡献率的时候多个贡献程度较大的传感器纠缠在一起，很难判断出哪个传感器贡献率最大。自适应PCA虽然可以较精确地定位故障传感器，但仍然无法抵抗噪声的干扰，导致无法定位故障数据的具体位置，其诊断结果不能用来为后期数据维护做参考。笔者提出的改进MSPCA模型可以较好地抵抗噪声带来的干扰，分段处理数据也使得主元和控制限可更灵活地变动，因此在两个监控图中其控制限参数是变动的。从二维贡献图中可以看出传感器6、7故障明显，与实际故障相符。计算模型的误报率、错报率和准确率如表1所示。

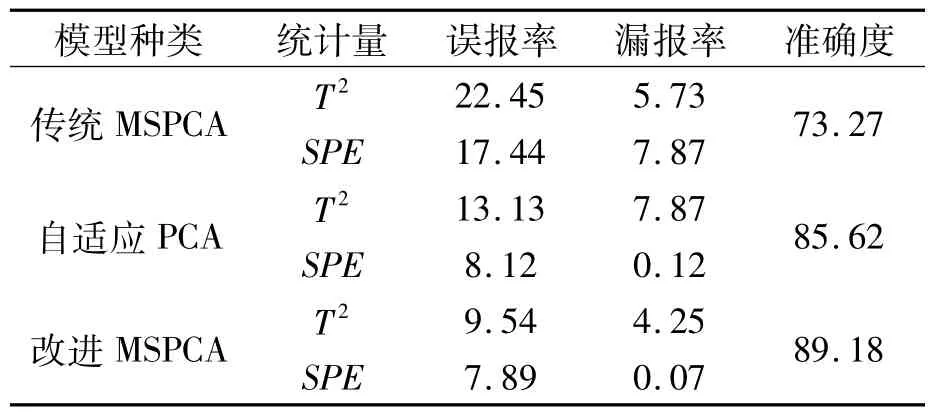
表1 故障检测结果准确度对比 %

通过实验结果可知:笔者提出的模型可以抵抗噪声干扰，有效地进行故障检测与分离，利用二维贡献图的辅助，可直观地评价传感器故障的相对严重程度;相比传统MSPCA和自适应PCA，笔者模型的准确率提高了21.71%和4.16%。

4 结论

笔者针对传统MSPCA及自适应PCA在故障诊断中存在的不足，提出了一种改进方法。通过对交通线圈检测器故障诊断实验分析可知，该模型可以有效地分离故障数据并对其故障相对严重程度进行评价，故障的分离可以为后期数据修补等工作提供依据，而故障的评价对后期故障决策也能够提供帮助。

［1］周东华.数据驱动的工业过程故障诊断技术［M］.北京:科学出版社，2011:2－11.

［2］BAKSHIBR.Multiscale PCA with application tomultivariate statistical process monitoring［J］.Aiche Journal，1998，44(7):1596 －1610.

［3］ROSELL J，SUÁREZR P.A path planning for grasping operations using an adaptive PCA－based sampling method［J］.Autonomous Robots，2013(1):1 －10.

［4］ALAEIH K，SALAHSHOOR K，ALAEIH K.A new integrated on－line fuzzy clustering and segmentation methodology with adaptive PCA approach for process monitoring and fault detection and diagnosis［J］.Soft Computing，2013，17(3):345 －362.

［5］DONOHO D L.De － noising by soft－ thresholding［J］.IEEE Transactions on Information Theory，1995，41(3):613－627.

［6］赵瑞珍.小波理论及其在图像、信号处理中的算法研究［D］.西安:西安电子科技大学图书馆，2001.

［7］WANG H，SONG Z.Statistical processmonitoring using improved PCA with optimized sensor locations［J］.Journal of Process Control，2002(12):735 －744.

［8］LIY.Fault detection and isolation based on abnormal sub － region using improved PCA［J］.Journal of Chemical Engineering of Japan，2004，37(4):514 －522.

［9］DUNIA R，QIN S J，EDGAR T F，et al.Use of principal component analysis for sensor fault identification［J］.Computer and Chemical Engineering，1996(20):713 －718.

［10］胡友强.数据驱动的在线MW_MSPCA故障诊断［J］.重庆大学学报，2012，35(4):100 －106.

［11］张德丰.Matlab小波分析与工程应用［M］.北京:国防工业出版社，2009:20－53.