车载压电悬臂梁结构参数对其发电量的影响
郑银环,黄 磊,王松伟,李玉峰,赵 燕
(武汉理工大学机电工程学院,湖北武汉430070)
压电发电装置利用压电材料的机电转换性能,可将环境中存在的各种机械能量转化为电能,从而为低耗能的电子产品供能[1-4]。车载环境中应用微电子装备愈来愈多,车载传感网络应用日愈广泛。由于传感网络中大量的传感器应用,使得对传感元器件的供电有一定的要求。采用压电发电装置,利用车辆行驶过程中的振动能、压力能,将其转化为电能储存起来,长期为传感元器件供电,使绿色能源代替化学电池成为了可能。
压电振子的结构形式主要有悬臂梁形和圆盘形,悬臂梁形压电振子具有低频和效率高等优点而被广泛研究[5-7]。国内外已有的研究表明,压电振子的固有频率与振动源的振动频率接近,产生共振时,压电振子的发电量最大[8-9]。因此压电悬臂梁的结构参数变化最终会影响压电装置的发电量。在已有的研究中,压电悬臂梁的振动模型建立在不考虑压电梁搭载物的简化条件中,实际上压电装置的搭载环境会对压电梁的响应产生重要影响,从而影响其机电转换效率。因此,笔者针对车载环境,分析压电梁结构参数变化对其固有频率和输出电压的影响规律,以期获得最大的发电量,提高有限体积压电梁在具体工作环境中的发电能力。图,其由金属基板、质量块、压电片和支座组成。金属基板上、下表面粘贴压电片。悬臂梁的一端固定在支座上,另一端随着环境的振动源自由振动。由于外界振动将引起悬臂梁的受迫振动,导致悬臂梁发生弯曲变形,进而引起压电层内应变和应力的变化。根据压电学理论,当压电振子自由端受外力作用而产生弯曲变形时,其表面便有电荷生成[10]。

图1 带质量块的压电悬臂梁结构示意图
为得到悬臂梁各参数对梁的固有频率及电压的影响,须选取适当的压电晶体片。因研究对象的载体为汽车,应用的场合是各电子元器件,因此压电发电装置较小,在满足供电的同时,应满足安装空间的要求。选取ZnO压电材料作为压电片,选取铍青铜作为悬臂梁的基板材料。
将悬臂梁简化为如图2所示的模型,设压电层的长度le等于梁的长度lb。
根据第一类压电方程,压电层所受应力及产生电场的关系可表示为:
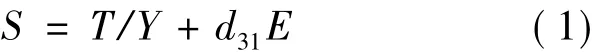
1 压电悬臂梁建模
图1为带质量块的压电悬臂梁的结构示意
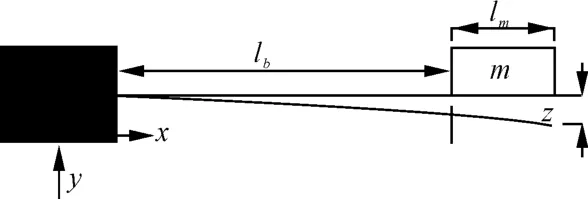
图2 压电悬臂梁简化模型

式中:S和T分别为应变和应力;D和E为电位移和电场强度;1/Y、d31和ε分别为压电片的柔度系数、压电常数和介电常数。
由于压电方程式与应力、应变直接有关,因此悬臂梁建模直接采用应力应变计算。
笔者研究的压电悬臂梁基本参数如表1所示,m为悬臂梁自由端质量块的质量,lm为质量块沿悬臂梁x方向的长度,lb为压电悬臂梁的长度,w为压电悬臂梁的宽度,tc为压电层厚度,tsh为中间金属层的厚度。

表1 压电悬臂梁初始参数
2 压电悬臂梁结构参数对固有频率的影响
当环境振动频率等于悬臂梁固有频率时,将引起悬臂梁的共振,压电层应力和应变的变化最大,从而使压电输出电压的变化达到最大。根据研究可知,车载环境下路面-车辆耦合振动的频率范围为0~20 Hz。
在表1所示的压电悬臂梁初始条件下,可以得到压电悬臂梁的固有频率和电压,如图3所示。由图3可知,在初始条件下仿真得到的压电悬臂梁的固有频率处在车身耦合振动的频率范围之内。因此可通过改变悬臂梁的结构参数来设计压电悬臂梁结构,使其固有频率处于0~20 Hz内,以使悬臂梁处于共振状态,具有最大的功率输出,从而满足车载压电发电要求。

图3 初始条件下压电悬臂梁的频率与电压关系曲线
图4 ~图7为仿真得到的压电悬臂梁各结构参数对固有频率的影响。由图4~图7可知,悬臂梁的固有频率随着自由端质量块质量、振子长度lb的增加而减小;随着压电振子宽度的增加,悬臂梁的固有频率基本成线性趋势增加;随着中间金属层厚度的增加,悬臂梁的固有频率也随之增加,且频率的变化范围较大,可见金属层厚度tsh对压电悬臂梁的固有频率有较大影响。为提高压电发电装置的发电效率,需获得较低的固有频率以满足环境低频振动的要求。因此设计悬臂梁压电发电装置时,在考虑悬臂梁自由端能承受的最大质量以及悬臂梁长度不宜过长的前提下,可通过适当增加质量块的质量和振子长度来降低频率,选择宽度较窄、金属层厚度尽量薄的悬臂梁结构。

图4 质量块质量m对悬臂梁固有频率的影响

图5 振子长度lb对悬臂梁固有频率的影响
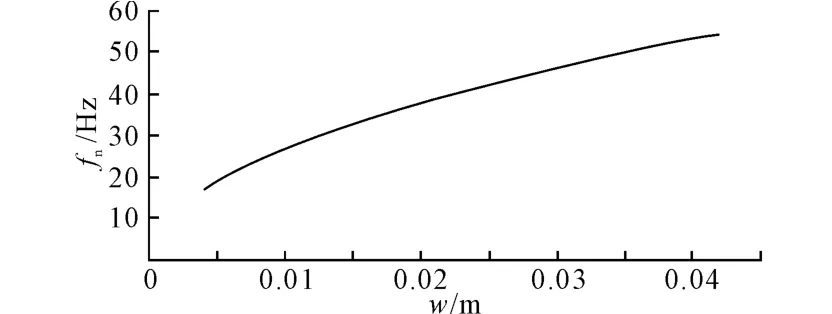
图6 悬臂梁宽度w对悬臂梁固有频率的影响

图7 金属层厚度tsh对悬臂梁固有频率的影响
3 压电悬臂梁结构参数对输出电压的影响
根据压电悬臂梁的理论模型,在一定的激振频率下,对悬臂梁的相关各参数与电压和频率之间的关系进行Matlab仿真分析。图8~图13为各结构参数与输出电压的关系图。
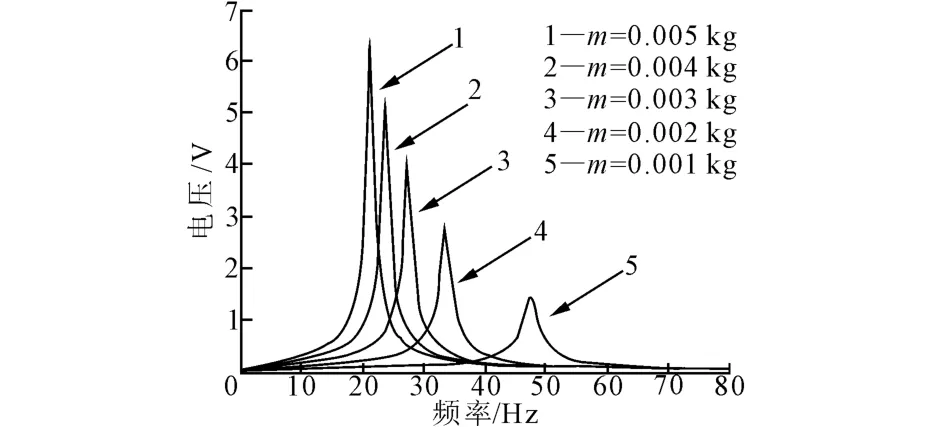
图8 质量块质量m与峰值电压和固有频率的关系

图9 悬臂梁的长度lb与峰值电压和固有频率的关系

图10 质量块沿悬臂梁x方向的长度lm与峰值电压和固有频率的关系

图11 悬臂梁压电层的厚度tc与峰值电压和固有频率的关系

图12 悬臂梁的宽度w与峰值电压和固有频率的关系
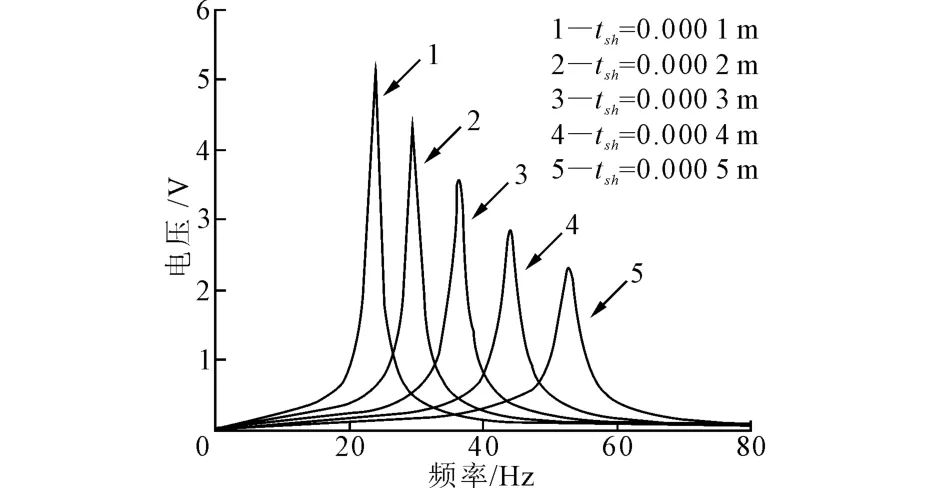
图13 中间金属层厚度tsh与峰值电压和固有频率的关系
由图8~图13可知,增加质量块的质量m、增加悬臂梁的长度lb、增大质量块沿悬臂梁x方向的长度lm均可以减小悬臂梁的固有频率,增大峰值电压。增加压电层的厚度、增加悬臂梁的宽度、增加中间金属层的厚度,悬臂梁的固有频率均随之增大,但峰值电压随之减小。且压电层厚度增加时,固有频率的变化范围很大;宽度增加时,峰值电压的幅值变化较大;中间金属层的厚度增加时,固有频率变化范围约为30 Hz。可见压电层厚度、中间金属层厚度对悬臂梁压电发电装置的影响都较大。
但在实际情况中,考虑到悬臂梁自由端的实际承载能力,质量块的增加必须保证悬臂梁在静态和动态环境下不受损害。对于微型悬臂梁压电发电装置,若要获得较低的悬臂梁固有频率和合适的电压,悬臂梁的长度是有限制的。质量块沿悬臂梁x方向的长度lm也受限,最大长度为lm=lb。
因此结构设计时,可适当增大悬臂梁自由端质量块的质量和悬臂梁的长度,减少悬臂梁的宽度和中间金属层的厚度,使压电悬臂梁的固有频率减小,接近环境振动源的低振动频率,使压电输出电压达到最大,从而获得最大的发电量。
图14为压电层和金属层的弹性模量比η与峰值电压和固有频率的关系。当弹性模量比增大时,悬臂梁压电发电的峰值电压有所减小,但是幅度较小,同时固有频率的变化幅度也较小。由此可知,压电层和金属层的弹性模量比对悬臂梁压电发电的影响较小,可将重点集中在悬臂梁的结构参数上。
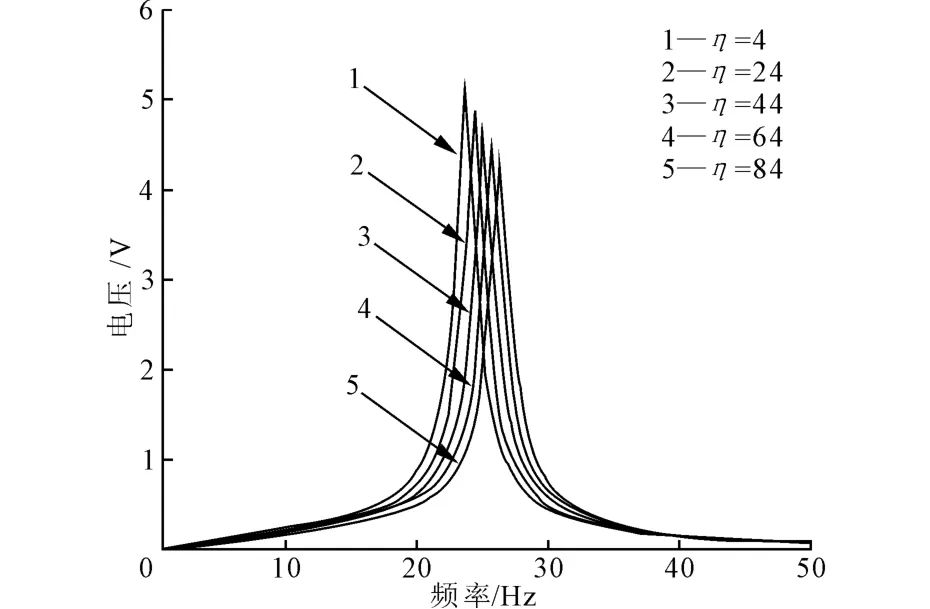
图14 弹性模量比η与峰值电压和固有频率的关系
4 结论
根据压电方程建立了悬臂梁压电发电的等效模型,通过计算机仿真,分析了车载环境下压电梁结构参数变化对其固有频率和输出电压的影响规律。研究结果表明:增加质量块的质量、增加悬臂梁的长度、增加质量块沿悬臂梁x方向的长度,悬臂梁的固有频率均随之减小,同时峰值电压随之增大;随着压电层厚度的增加、悬臂梁宽度的增加、中间金属层厚度的增加,悬臂梁的固有频率均随之增大,峰值电压随之减小;悬臂梁的固有频率随压电层和金属层的弹性模量比的增加而增大,峰值电压随之减小,但是幅度都较小,影响不是很显著。因此设计压电悬臂梁时,可适当增大悬臂梁自由端质量块的质量和悬臂梁的长度,减少悬臂梁的宽度和中间金属层的厚度,使压电悬臂梁的固有频率减小,以满足环境低频振动的要求,引起悬臂梁的共振,使输出电压增加,从而提高压电装置的发电效率。
[1]阚君武,唐可洪,任玉,等.压电单晶梁发电机的能量效率[J].光学精密工程,2008,16(12):2398 -2405.
[2]袁江波,单小彪,谢涛,等.悬臂梁单晶压电发电机的实验[J].光学精密工程,2009,17(5):1072-1077.
[3]邓冠前,陈仲生,陶利民,等.基于压电机械能量捕获行为研究[J].压电与声光,2009(6):939-942.
[4]马玉龙.悬臂梁压电发电技术研究[J].装备制造技术,2009(2):11-12.
[5]刘辉,韩树人,何鹏举,等.压电悬臂梁采收振动能发电能力分析与仿真[J].矿山机械,2011,39(3):98-102.
[6]姜德龙,程光明,曾平,等.悬臂梁双压电晶片振子发电性能研究[J].机械设计与制造,2011(1):121 -123.
[7]赵鼎成,许来涛,韩龙伸,等.压电悬臂梁发电性能与试验研究[J].环球市场信息导报,2012(30):64 -65.
[8]阚君武,唐可洪,王淑云,等.压电悬臂梁发电装置的建模与仿真分析[J].光学精密工程,2008,16(1):71-75.
[9]袁江波,谢涛,单小彪,等.复合型悬臂梁压电振子振动模型及发电试验研究[J].机械工程学报,2010,46(9):87 -92.
[10]袁江波,谢涛,陈维山,等.悬臂梁压电发电装置的实验研究[J].振动与冲击,2009,28(7):69 -72.

