用动能定理研究滑动摩擦力作用下弹簧振子振动的终态位置和振动路程

张多生

(甘肃省武威第六中学 733000)

如图1所示，劲度系数为k的一根轻质弹簧，左端固定在竖直墙壁上，右端连接一质量为m的小物块，开始时弹簧处于原长，小物块静止于O点.将小物块向右拉至A点，释放后小物块在粗糙水平面上左右振动起来.此装置称之为弹簧振子，小物块称为振子.由于摩擦，小物块最终会停下来.已知小物块与水平地面间的动摩擦因数为μ，最大静摩擦力可看成滑动摩擦力的大小，为μmg.对于振子最终停留的位置，好多同学错误地认为一定停在O点.从动力学角度研究滑动摩擦力作用下弹簧振子的运动规律，高中学生限于数学知识，难于理解.本文从能量的角度探索滑动摩擦力作用下弹簧振子的运动规律，确定振子最终停留的位置及振动通过的路程.

一、平衡位置

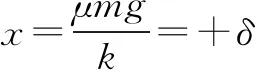
二、振子单向运动过程中相对于O点的最大位移的变化

弹力是变力，弹力做的功可以通过F-x图象的“面积”求解.振子从O点运动到A点的过程中，弹簧的形变量等于小物块的位移x，则弹力F随位移x的关系为F=kx,F-x图象如图3所示.此过程中克服弹簧弹力F所做的功W为图象与x轴围成的面积，即

以弹簧自然伸长时振子的位置O为原点，建立直线坐标系，如图4所示.把振子从右端最大位移x0处无初速释放，振子开始左右振动.设x1、x2、x3、x4…依次为振动过程中振子离O点的最大位移.

振子沿ox轴负方向从x0处运动到x1(x1<0)处的过程中，由动能定理得出：

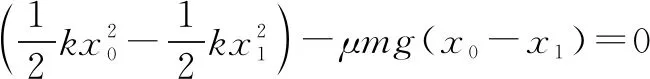
整理可得：

振子在x1处掉头而回，沿x轴正方向运动，到达x2处的过程中，由动能定理继续得出：

整理可得：

至此不难看出，只要我们交替运用(1)式和(2)式，就可以知道振子偏离O点的最大位移变化规律：

当振子向左运动时有：

x0+x1=x2+x3=x4+x5=…=2δ

当振子向右运动时有：

x1+x2=x3+x4=x5+x6=…=-2δ

即小物块每经过一个单向运动后，对O点的最大位移大小按等差数列的规律递减，递减公差为2δ，即：

x0-|x1|=|x1|-x2=x2-|x3|=…=2δ(3)

以上结论对最后一次单向运动可能不适用.最后一次单向运动有两种可能性，如图5和图6所示.若最后一次单向运动途经0点，(3)式仍然成立；若最后一次单向运动只在O点一侧运动，不经过O点，则最大位移大小之后为2δ.

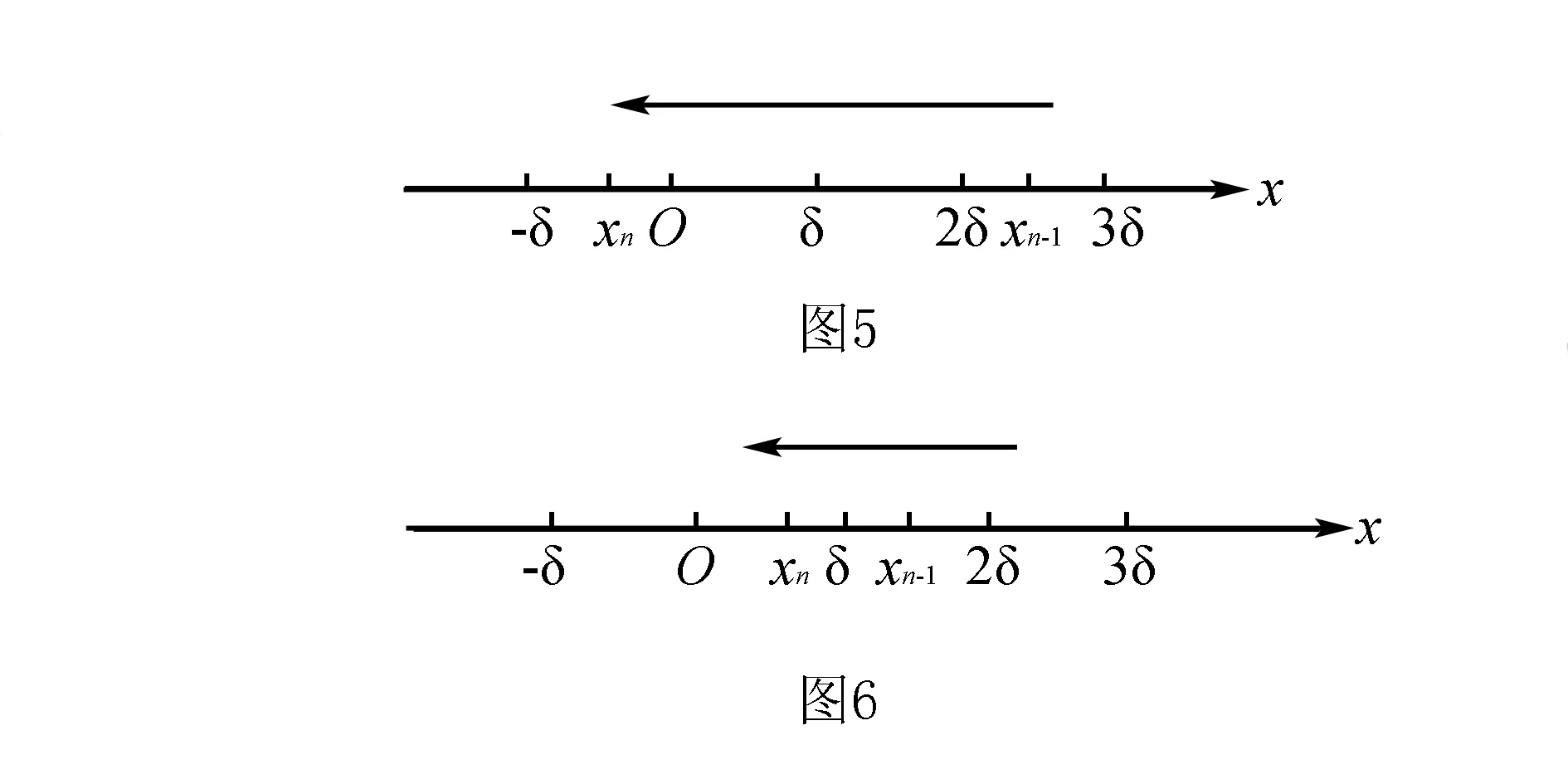
三、振子最终停留位置

由(1)式和(2)式交替应用，可确定出振子运动过程中离O点的最大位移值，依次为

x0，x1=-(x0-2δ)，x2=x0-4δ，x3=-(x0-6δ)，…….

若振子经过n个单向运动后静止，由以上规律可递推出振子最终静止的位置，为xn=(-1)n·(x0-2nδ)

到此，我们还没有彻底确定振子的终态位置，还需要确定单向运动次数n.通过上面的分析研究可知

|xn|≤δ，δ<|xn-1|≤3δ

因x0-2nδ不一定大于零，由|xn|≤δ求解n比较麻烦.而x0-2(n-1)δ一定大于零，则

δ

在以上范围内取符合条件的自然数n，即为振子单向运动的次数.n确定后，振子的终态位置也就确定了.

四、振子运动的路程

振子运动路程用逐段位移大小之和求得.参考最后一次单向运动情况(图5和图6)，可得出以下结果：

s=x0+2|x1|+2x2+…2|xn-1|+|xn|

=x0+2(x0-2δ)+2(x0-4δ)

+…2(x0-2(n-1)δ)+|x0-2nδ|

或s=x0+2|x1|+2x2+…2|xn-1|-|xn|

=x0+2(x0-2δ)+2(x0-4δ)

+…2(x0-2(n-1)δ)-|x0-2nδ|

五、结论应用

在x0比δ不太大的情况下，套用上述规律计算终态位置和路程反而比较麻烦.采用递推的办法，思路比较清晰.根据振子对O点的最大位移大小递减规律(公式(3))，依次写出最大位移值，数出单向运动次数n，再计算振子运动的路程.比如，当x0=7.5δ时，最大位移依次为

7.5δ，-5.5δ，3.5δ，-1.5δ，-0.5δ

可知振子最终停留在x=-0.5δ处，单向运动次数为n=4.结合运动示意图求出的路程为s=7.5δ+2×5.5δ+2×3.5δ+2×1.5δ-0.5δ=28δ

在x0比δ大的多的情况下，就得推理最大位移的变化规律，确定单向运动次数，再用数列知识求路程.