“近似法”在简谐运动中的应用

彭爱国 彭宇琪

(武汉市第三中学 湖北 武汉 430050)

在高中物理竞赛中经常出现要近似处理的试题，特别是在证明简谐运动中经常出现.由于很多学生不熟悉“代数近似”的公式,不能灵活应用“小量近似”，从而不能突破问题的瓶颈，致使问题无法正确求解.近似处理通常有代数近似和几何近似这两种方法，本文以第34届全国中学生物理竞赛预赛第16题为例谈谈代数近似法和几何近似法在具体问题中的应用.

【题目】如图1所示，两劲度系数均为κ的同样的轻弹性绳的上端固定在一水平面上，下端悬挂一质量为m的小物块.平衡时，轻弹性绳与水平面的夹角为α0，弹性绳长度为l0．现将小物块向下拉一段微小的距离后从静止释放.

(1)证明小物块做简谐振动；

(2)若κ=0.50 N/m,m=50 g,α0=30°,l0=2.0 m，重力加速度g=9.8 m/s2，求小物块做简谐振动的周期T；

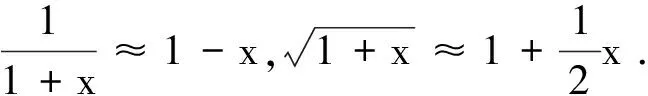
图1 题图

方法1：代数近似法

解：(1)取小物块的平衡位置为原点O，y轴的正方向竖直向下，如图2所示.

图2 方法1分析图

由牛顿第二定律可知

ma=mg-2κ(l-L)sinα

(1)

式中a为物块的加速度，L为弹性绳的原长,l和α分别为物块离开平衡位置的位移为y时弹性绳的长度和弹性绳与水平面的夹角.

由几何关系得

(2)

(3)

d=l0cosα0

(4)

式(4)代入式(2)展开，化简得

由于y是小量，y2是二阶小量，可略去.得

l=l0+ysinα0

(5)

将式(5)代入式(3)，得

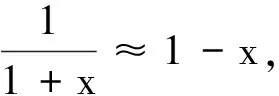
忽略y2项，得

l0sinα=l0sinα0+ycos2α0

即

(6)

当小物块处在平衡位置时有

mg=2κ(l0-L)sinα0

即

(7)

式(5)、(6)、(7)代入式(1)，消去l，L，sinα，得

ma=mg-

略去y2项

由简谐运动的特征方程知F回=-Ky，所以

因此，当y很小时，小物块做简谐运动.

(2)小物块做简谐运动的周期为

(8)

将题给数据代入式(8)得T=1.8 s.

(3)因将小物块拉开距离y0=0.010 m 时从静止松手，故小物块做简谐振动的振幅A=0.010 m.

初始时，小物块速度为零，小物块位于最大位移处，其初相位为

φ0=0

(9)

圆频率为

故在国际单位制中，小物块做简谐振动的方程为

y=0.010cos(3.5t)

方法2：几何近似法

解：(1)如图3所示，过O作OC⊥AO′,交AO′于点C,因y极小,所以∠OAC极小, 所以∠AOC≈90°，即∠COO′≈α0，则有

l=l0+ysinα0

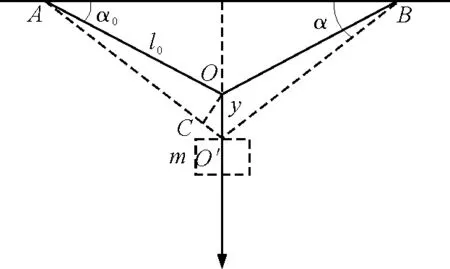
图3 方法2分析图

当小物块处在平衡位置时有

mg=2κ(l0-L)sinα0

即

取竖直向下为正方向，当物块离开平衡位置一微小位移y时，则回复力

F回=mg-2κ(l-L)sinα

将l,sinα,L代入上式得

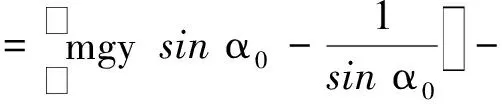
分子中忽略y2项,分母中忽略y项,得

所以小物块做简谐运动.

(2)、(3)问同上.

此题方法1用代数近似法，过程比较繁难，对学生的数学能力要求较高,一般学生不容易推导出简谐运动的特征方程F回=-Ky，但用几何近似法则省去了大量的代数推导，只用到最基本的小量近似就可得到简谐运动特征方程.所以,对这类问题，我们应优先考虑几何近似法.