一个电磁感应问题解答的探讨

叶惠芳 林辉庆

(杭州市余杭高级中学 浙江 杭州 311100)

1 一个电磁感应问题及常见解答

【题目】如图1所示，两足够长的光滑平行金属导轨MN和PQ间的距离L=0.4 m，金属导轨所在平面与水平面的夹角θ=37°，M和P间连接电阻R=2.0 Ω，质量m=0.04 kg，电阻r=3.0 Ω的金属棒AB垂直放置在导轨上，与导轨接触良好且与MP距离x0=0.5 m.在MPNQ区域有垂直于导轨向上随时间变化的匀强磁场，已知t=0时刻磁感应强度B0=0.5 T,若此刻无初速释放金属棒AB，它将沿导轨匀加速下滑.已知sin 37°=0.6,cos 37°=0.8.试求：

(1)金属棒匀加速下滑的加速度大小；

(2)从t=0时刻开始磁感应强度B随时间t应如何变化.

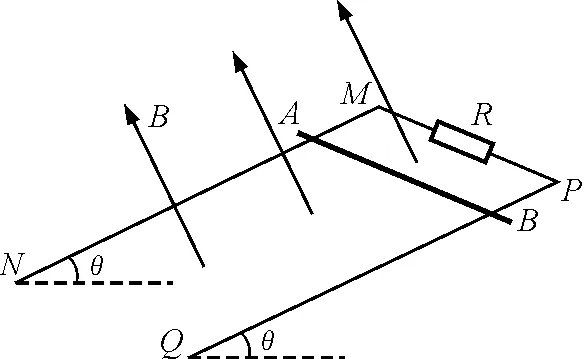
图1 题图

常见解答：AB能匀加速下滑，则可知电路中的感应电流为零，故其加速度

a=gsin37°=6 m/s2

由电路中感应电流为零可知感应电动势为零，回路中磁通量不发生变化，即

解得

(1)

2 对常见解答的质疑

常见解答隐含着如下的矛盾：在t=0时刻，AB速度为零，不切割磁感线，则动生电动势E动为零，但磁感应强度B随时间t是变化的，因此可能会产生感生电动势，这样回路中就可能会有感应电流，导体棒AB可能会受安培力作用，不会以加速度a=gsinθ下滑.

让我们来计算一下t=0时感生电动势E感的大小

虽然这里验证了当磁感应强度B随时间t以式(1)变化，AB以a=gsinθ匀加速下滑，但这里仍存在更普遍的问题：如果B随时间按其他方式变化，AB是否也能以其他加速度匀加速下滑？

3 对一般解答的探讨

设磁感应强度B以B=B(t)方式变化，AB以加速度a匀加速下滑，AB与MP的距离

t时刻的磁通量为

Φ=LxB

感生电动势为

感应电流为

AB棒所受的安培力

FA=BIL

由牛顿第二定律有

mgsinθ-FA=ma

联立以上各式解出

(2)

代入有关数据得到

(3)

从理论上讲，对任何一个a值，由式(3)都能求出对应的B=B(t).

把a=gsinθ代入式(2)得到

化为

对上式两边积分即可得到

(4)

其中C是积分常数.将t=0时,B=B0=0.5 T代入上式，即得C=0.25 T·m.

可见当a=gsinθ时式(1)只是式(3)对应的一个特殊解.

让我们再看另一种特殊情况，即a=0，导体棒AB静止在导轨上，式(2)为

化为

mgsinθ(R+r)dt=BL2x0dB

解出

(5)

在一般情况下，式(2)是非线性微分方程，我们无法由它求出B(t)的解析式.但我们可以根据这个方程，用微元数值计算法得到函数B=B(t)对应不同时刻(例如每隔Δt=0.01 s)的B值，并由此作出B-t图像.

(6)

求出

在t1=0.01 s时

0.5 T+10×0.01 T=0.6 T

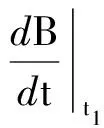
(7)

求出

在t2=0.02 s时刻

0.6 T+8.282×0.01 T=0.683 T

(8)

求出

同理求出以后各时刻的B值如表1所示.

表1 a=4 m/s2时各时刻对应的B值

作出B-t图像如图2所示.

图2 a=4 m/s2时的B-t图像

假如要使棒AB静止释放后以5 m/s2的加速度向上运动，即取a=-5 m/s2，同理可以求出对应的B=B(t)在不同时刻的值，如表2所示.

表2 当a=-5 m/s2时各时刻对应的B值

作出B-t图像如图3所示.

图3 a=-5 m/s2时的B-t图像

用同样的方法可以求出对应棒AB以任一加速度运动，磁感应强度B随时间t的变化方式.

4 结论

通过上面的研究知道，常规解法得到的结果，只是一个特殊解，并不是这个问题的唯一解.实际上，只要磁场以恰当的方式变化，导体棒能以任一加速度沿导轨向下匀加速运动，也能以任一加速度沿导轨向上匀加速运动，还可以保持静止不动.