浅谈微小物理量近似求解的方法——对浙江省2016年物理选考第23题第(3)问的分析探讨

沈 卫

(湖州市菱湖中学 浙江 湖州 313018)

浙江省2016年物理选考第23题的第(3)问是一个典型的微小物理量计算问题.其最后一问描述出了每秒打到探测板上每个位置离子的动量均不同，但呈现线性变化的问题，然而在具体给出的参考答案中却把计算过程极尽精简化，没有体现出这一特点，使不少考生颇为疑惑.本文将从图像面积求解这个角度来对线性变化的离子动量计算给出分析论证.

1 浙江省2016年物理选考第23题真题以及参考答案

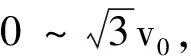
(1)求离子束从小孔O射入磁场后打到x轴的区间；

(2)调整磁感应强度的大小，可使速度最大的离子恰好打在探测板右端，求此时的磁感应强度大小B1；

(3)保持磁感应强度B1不变，求每秒打在探测板上的离子数N,若打在板上的离子80%被吸收，20%被反向弹回，弹回速度大小为打板前速度大小的0.6倍，求探测板受到的作用力大小.

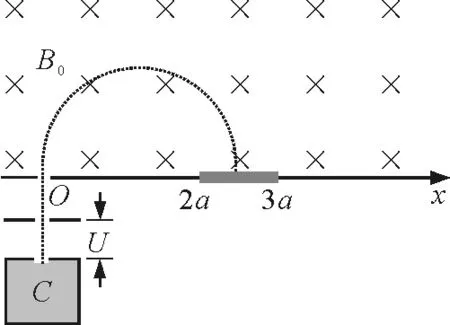
图1 题图

参考答案：(1)根据动能定理，可得

由

可得

v0≤v≤2v0

离子在磁场中运动

离子打在x轴上的坐标表达式为

代入数据得

2a≤x≤4a

(2)当速度最大的离子打在探测板右端

(3)离子束能打到探测板的实际范围为

2a≤x≤3a

对应的速度范围为

每秒打在探测板上的离子数为

由动量定理，吸收的离子受到板的作用力大小

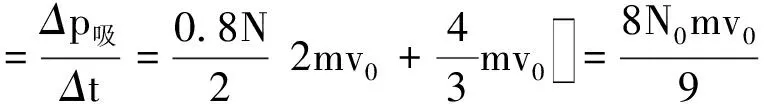
反弹的离子受到板的作用力大小

根据牛顿第三定律，探测板受到的作用力大小

2 对于选考23题第(3)问“探测板受力”的分析探讨

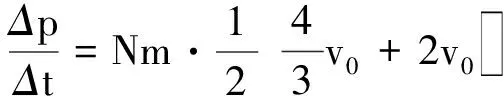
把探测板分成无穷多的小段Δx，每小段都足够的小，那么可以认为打到每小段Δx上的离子速度是相同的.再任意取一个小段Δx，设为A点，令离子进入磁场的位置O到A的距离为x，得到如图2所示的示意图.

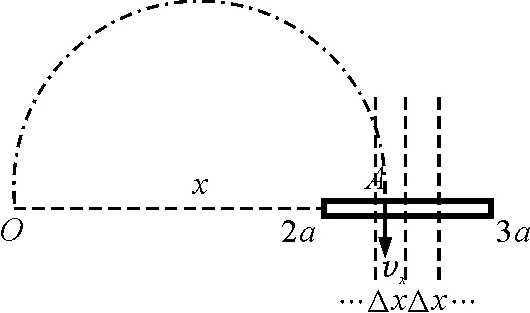
图2 离子在磁场中做匀速圆周运动的示意图

x的取值范围为2a～3a，且有打到A点的离子速度vx满足

即有

因此可认为探测板上A点所在处Δx范围内的离子速度相同，且在Δx范围内每秒打到板上的离子数目

则在这个长度微元Δx范围内，打到探测板上离子的动量为

如此可将探测板上每个长度微元中离子的动量表示出来，再进行累加，便可获得每秒钟内打到板上离子的总动量

p总=Δp1+Δp2+Δp3+…=

令

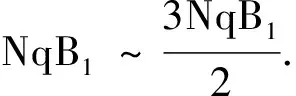
所以y的取值范围就是

故可作y与x的正比函数关系图如图3所示.

图3 y与x的正比函数关系图

由总动量p总的累加计算公式与y-x图像，不难发现，y-x图像中正比例图线与两个坐标轴在x轴的2a～3a范围内所围梯形(阴影部分)的面积即为单位时间内打到探测板上离子的总动量p总.

每秒打到板上离子的总动量

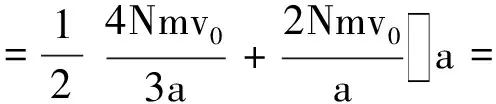
再根据题目条件与动量定理可求得探测板受到的作用力

3 结束语

通过将探测板分解为一个个长度微元，把呈线性变化的物理过程经过细分成为一个个恒定不变的过程，化变为恒，在这里所体现出的无限分割思想使原本复杂的过程变得简单而直观.将这一系列的小过程进行累加求和，让小量求和的过程以直观的图像面积计算呈现出来，使这种极限求和得以用考生所熟知的数学方法解决，从而帮助考生正确认识与理解解决物理问题的有效手段与途径.