另解2017年全国物理竞赛预赛第16题
费新良 沈 卫
(菱湖中学 浙江 湖州 313018)
1 试题回放与参考解析
2017年第34届全国中学生物理竞赛预赛的最后一题,原题如下.
【题目】如图1所示,两劲度系数均为κ的同样的轻弹性绳的上端固定在一水平面上,下端悬挂一质量为m的小物块.平衡时,轻弹性绳与水平面的夹角为α0,弹性绳长度为l0.现将小物块向下拉一段微小的距离后从静止释放.
(1)证明小物块做简谐运动;
(2)若κ=0.50 N/m,m=50 g,α0=30°,l0=2.0 m, 重力加速度g=9.8 m/s2, 求小物块做简谐运动的周期T;


图1 原题附图
参考答案给出的解法如下.
解析:(1)取小物块的平衡位置为原点O,y轴的方向竖直向下,如图2所示.由牛顿第二定律可知
ma=mg-2κ(l-L)sinα
(1)
式中a为小物块的加速度,L为弹性绳的原长,l和α分别为小物块离开平衡位置的位移为y时弹性绳的长度和弹性绳与水平面的夹角.由几何关系有
(2)
(3)
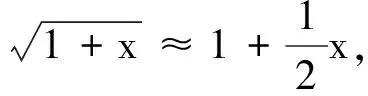
l=l0+ysinα0
(4)

l0sinα=l0sinα0+ycos2α0
(5)

图2 原题解析用图
当小物块处在平衡位置时有
mg=2κ(l0-L)sinα0
(6)
即
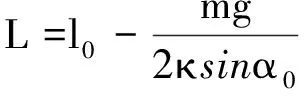
(7)
将式(5)、(6)、(7)代入式(1),略去y2项,可将式(1)化成

(8)
上式右端括号中的量是大于零的常量,式(8)可表示为
ma=-mω2y
(9)
式中
(10)
式(9)是简谐振动的动力学方程.因此,当y很小时,小物块做简谐振动.
第(2)、(3)两小题的解答从略.
点评:参考答案给出的解法是建立在微元思想和小量近似思想上的,可以避开高等数学的相关知识,而且有些学生在竞赛辅导时学习过微元思想和小量近似的相关知识.但高中的小量近似和微元思想都学习得不系统,也不常用,所以很多学生在用它解题时很难掌握其准确的用法,导致这个题目的得分不高.
2 利用导数再解此题
现鉴于高中数学已经初步学习了导数的相关知识,我们完全可以避开微元与小量思想,从学生熟悉的导数入手来解这个题目.利用导数知识对这道题的解法如下.
解析:如图3所示,小物块平衡时,满足方程
mg=2κ(l0-L)sinα0
其中L为弹性绳的原长,l0和α0分别为小物块在平衡位置时弹性绳的长度和弹性绳与水平面的夹角.可解得原长为

图3 利用导数求解用图
现将小物块向下拉一段微小位移dy至与水平面相距为y的位置,此时弹性绳的长度为l,绳与水平面的夹角为α,取竖直向下为正方向,此时小物块的受力关于y的函数为
F(y)=mg-2κ(l-L)sinα
对F(y)求导可得
并求在y=l0sinα0时的导数值为
可以把上式写成
即小物块从平衡位置向下偏移dy时的力
此式可写成
dF=-mω2dy
式中
此式为简谐振动的动力学方程.因此,当dy很小时,小物块做简谐振动.
点评:此方法不再需要用到小量近似,而是用到导数的知识来解决问题,在方法上更清晰明确,而计算上也更方便.而且导数在高中已经有系统的学习和训练,此题的这种解法不仅是对高中导数的应用,还可反过来进一步加深对物理的微元和导数的理解.笔者觉得此方法可在高中数学支持的基础上多加以应用.

