初高中数学衔接知识及思想方法探究之复合函数问题

刘浩州

(福建省泉州实验中学 320006)

“衔接”意指将两个分开的物体间的连接，这里指初中和高中数学的教学内容和数学思想方法上的连接.但并不意味着将高中的知识内容提前教学或者把高中的试题放在初中考查，而是从高中教学内容和数学思想的刚性需求出发，研究初中阶段应该渗透的数学思想以及知识预备，然后在初中的教学中以及初中学业结束后在衔接内容上设置合适的题目或者知识点.事实上，初高中教学的衔接不仅仅关注显性的知识，更应关注蕴涵在知识中的数学思想，关注引导学生逐步形成适应高中数学教学的学习习惯和思维方式.本文例举的例题主要是复合函数部分内容，可以变式为衔接阶段的试题也可以作为高中阶段复合函数专题训练的案例.

一、例题及解析

例1已知函数f(x),g(x)：

x0123f(x)2031

x0234g(x)2103

则函数y=f(g(x))的零点是( ).

A.0 B.1 C.2 D.3

答案：C

复合函数经常使用换元法对某个整体进行换元，方便计算也方便理解.本题考查的一个主要能力是对换元的使用，不管所求目标函数多复杂，要先看到对应关系是“f”，求函数f(x)的零点，借助第一个表格找到f(t)=0的解为t=1，然后通过第二个表格找到t=g(x)=1，显然x=2.由于初中阶段的函数表示形式还没有学习映射概念，“零点”也没有学习过，但是换元法接触过，此题可以针对换元法为学生做好必要训练和知识预备.

变式：已知y是关于t的函数，t是关于x的函数，并且有以下条件：

t0123y2031

x0234t2103

则使得方程y=0成立的x的值是( ).

A.0 B.1 C.2 D.3

例2若方程2sin2x+sinx-m=0在[0,2π)上有且只有两解，则实数m的取值范围是____.

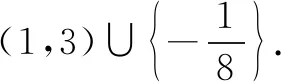
此题考查了对复合函数图象的理解，综合考查了高中数学思想方法中数形结合、化归与转化思想的应用.高中阶段的解题可以利用二次函数与三角函数的图象解决，也可以分离参数将方程的解转换为函数图象的交点.由于涉及的三角函数图象是初中学生所没接触过的，因此可以这样变式：

变式1关于x的方程2(-x2+2x)2-3(-x2+2x)+1=0的解的个数为____.

计算思维[1]的英文释义是Computational thinking，顾名思义，即是将计算机的思维用在人的思考里。拓展开来，便是我们用计算机的基础概念、计算方法、语言逻辑等去思考、设计和解决人的问题。

答案：3个

变式2若方程2(-x2+2x)2+(-x2+2x)-m=0在-1≤x≤3上有且只有两解，则实数m的取值范围是____.

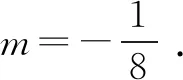
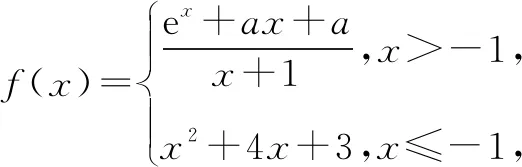
A.4个 B.7个 C.10个 D.12个

答案：D.

本题考查了分段函数的理解，充分考验了学生分类与整合的能力，同时也对复合函数有较大的能力要求.在学生了解了函数运用y=f(x)的表达形式之后可以考虑变式为：

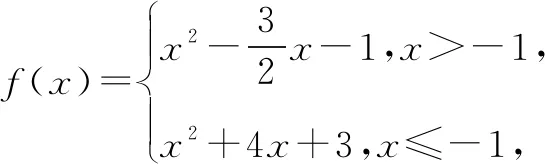
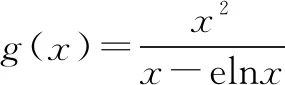
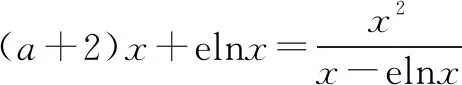
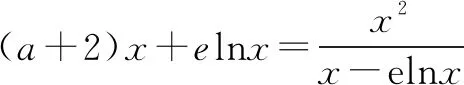
由二次方程根的分布及二次函数图象特征，设φ(t)=t2+(a+1)t-a-1，则

解得a>-1.

例4考查了将函数图象的“交点”问题转换为方程的解或者函数的零点，这是高中函数部分很重要的方法，也是数形结合融会贯通的一个表现.由于此题涉及的函数相对复杂，方法上运用的求导，较难直接变式成初中的题目，但是可以在高中复合函数教学中作为典型例题.

函数的知识及涉及的思想是初高中都必须掌握的内容，也是体现数学核心素养中数学抽象与逻辑推理的重要表现形式．例1作为基础的抽象函数，对培养学生数学抽象的素养有很大帮助，后面三道例题对培优学生逻辑推理的素养以及锻炼学生分类讨论、数形结合及转化与化归能力也有很大帮助.

二、总结

高中数学课程应注意提高学生的数学思维能力，这是数学教育的基本目标之一.教师作为学生建构主义学习的引导者，通过对知识和问题的形成过程的研究，设置帮助学生建构知识的题目，关注学生衔接过程中需要的知识，从而帮助学生运用所学知识和已有的经验主动建构富有意义的理解.这也是培优数学核心素养的一个重要方面.