一道高考题的解法探究

张 梅

(四川省成都市四川师范大学数学科学学院 610000)

普通高中数学课程标准(2017年版)提出高中数学阶段的数学教育培养目标是：会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界，从而提出了六大核心素养.高考题是以课程标准为依据，以选拔学生为目的而命制.解析几何是用代数方法研究解决几何问题的一门数学学科，渗透了一种重要的数学思想—数形结合思想，同时也是高考的热点之一.本文结合2018年高考数学全国卷Ⅲ文科第22题进行多重解法剖析.

一、试题呈现和分析

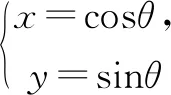
(1)求α的取值范围;

(2)求AB中点P的轨迹的参数方程.

立意分析本题以直线和圆这两种基本几何图形为载体.融合了斜率、倾斜角、直线与圆的位置关系、圆的参数、点的轨迹等知识点，同时有三角、二次函数等知识的交汇命题.注重考查学生的转化思想、数形结合思想、构造思想，分类讨论思想.同时考察了学生的发现问题，多角度解决问题的能力.

二、解法探索和分析

数学解题是学生学习数学的主要部分.数学解题练习的最终目的是为了培养数学思维通过对解法多角度的探索，积极引导学生的数学思维的碰撞.

第一个小问的解法探究：

解法1圆的普通方程为x2+y2=1.

圆的普通方程为x2+y2=1②.

解法分析解法1的思路是利用圆心到直线的距离d与圆的半径r之间的大小关系来计算直线与圆的位置关系，特别需要注意直线的斜率不存在的情况.

解法2的思路是联立直线的参数方程和圆的方程，同时避免了讨论直线斜率不存在的情况，灵活运用圆系方程解题，可以使计算量大大的减少.

解法3的思路利用数形结合思想，用代数的语言描述几何要素及其关系，构造两个直角三角形△OQM、△OQN，利用正弦求倾斜角，此法步骤简单.

第二个小问解法探究

圆的普通方程为x2+y2=1②.

(3)采用耐磨损、抗静电能力强的高分子塑料材料为基料加工的斜板，具有表面光滑疏水、抗静电、耐磨损的特殊效果，细泥物料不易在斜板板面粘结和堆积。

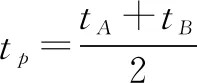
又∵tA、tB满足圆系方程②

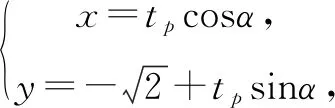
∵有两个交点,∴Δ=4k2-4>0,∴k<-1或k>1.

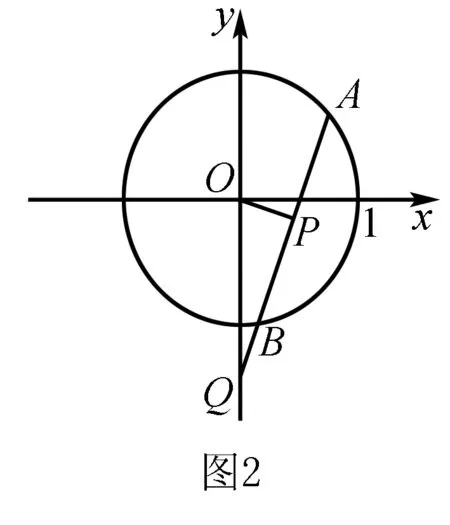
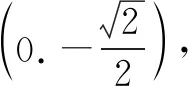
解法4如图2所示，设P(x,y),