探析传送带问题的求解方法
成金德
(浙江省义乌市东大门学校,浙江 义乌 322000 )
传送带是动力学中一类典型的物理问题,传送带与实际中的货物传递有着紧密的联系.由于传送带问题涉及受力分析、运动分析、匀变速运动规律、动力学规律,因此,传送带问题知识综合性强,应用能力要求高.对于一些初学物理的学生,以及一些分析能力不强的学生,求解传送带问题时,往往不知从何下手,不仅高呼难度太大,而且对学习物理产生了畏难情绪.基于此,探讨和分析传送带问题显得很有意义.
1 概念论述
小物块以初速度v0(v0≥0)在匀速运动的传送带上开始运动的力学系统可称为“传送带”模型.
实际中的传送带是利用货物和传送带之间的摩擦力来传递或运输货物的一种装置,它能将货物从一个地方运送到另一个地方.由于传送带问题涉及摩擦力的判断、运动状态的分析和运动学知识的应用,有些传送带问题包含的物理过程比较复杂,应用的知识综合性较强,因此,传送带问题不仅是物理教学上的一个难点,也是教学考查中的一个热点.
2 特点整合
2.1 水平传送带
(1)传送带以速度v做匀速运动,小物块以v0=0放上传送带.如图1所示.
在摩擦力作用下,小物块做匀加速直线运动,当小物块的速度大小等于v时,若小物块还没有运动到另一端,则小物块将与传送带一起做匀速运动.

图1 水平传送带(1)图
(2)传送带以速度v做匀速运动,小物块以初速度v0放上传送带.如图2所示.
若v0>v时,小物块在摩擦力的作用下,做匀减速直线运动,当小物块的速度降至v时,若小物块还没有运动到另一端,则小物块将与传送带一起做匀速运动;
若v0 (3)传送带以速度v做匀速运动,小物块以初速度v0放上传送带,与传送带相向运动.如图3所示. 图3 水平传送带(3)图 若v0>v时,小物块在摩擦力的作用下,做匀减速直线运动.若在速度减为零之前还没有从左边滑出,则小物块在摩擦力作用下向右做匀加速运动,当速度达到v后,小物块匀速从右端滑出; 若v0 (1)传送带以速度v做匀速运动,小物块无速度放上传送带,如图4所示. 在摩擦力作用下,小物块沿传送带斜向上运动. 若小物块的速度始终小于v,则小物块将一直做匀加速运动; 若小物块运动到传送带上端前速度达到v物=v,则小物块匀速向上运动. 图4 倾斜传送带(1)图 (2)传送带以速度v做匀速运动,小物块以初速度v0放上传送带,如图5所示. 若v0 若v0>v,则小物块做匀减速运动.当小物块运动到传送带上端前速度达到v物=v,若μ>tanθ,则小物块做匀速运动;若μ (3)传送带以速度v做匀速运动,小物块无速度放上传送带,如图6所示. 若小物块的速度始终小于v,则小物块将一直做加速运动; 若小物块运动到传送带下端前速度达到v物=v,且μ>tanθ,则小物接着做匀速运动; 若小物块运动到传送带下端前速度达到v物=v,且μ 图6 倾斜传送带(3)图 (4)传送带以速度v做匀速运动,小物块以初速度v0放上传送带,如图7所示. 若v0 若v0≥v,且μ=tanθ,则小物块一直做匀速运动; 若v0>v,且μ>tanθ,当小物块的速度始终大于v时,小物块做匀减速运动;当小物块到达底端前速度达到v物=v,小物块将做匀速运动. 若v0>v,且μ (5)传送带以速度v做匀速运动,小物块以初速度v0放上传送带,如图8所示. 图8 倾斜传送带(5)图 若μ 若μ=tanθ,小物块一直做匀速运动; 若μ>tanθ,小物块做匀减速运动;当小物块到达底端前速度达到v物=0,在摩擦力作用下小物块反向做加速运动;若小物块在到达顶端前速度达到v物=v,则小物块做匀速运动. 首先,由题给的初始条件,即依据小物块的速度v物和传送带速度v带间的关系,确定小物块的受力情况,从而确定小物块的运动情况; 其次,根据牛顿第二定律求出小物块的加速度; 再次,当小物块的速度与传送带的速度相等时,要注意分析小物块受到摩擦力的突变情况,这是求解传送带问题的一个关键点;若摩擦力发生突变,则需要由受力情况及牛顿第二定律再次求出小物块的加速度[1]; 第一,注意弄清小物块相对于传送带的运动方向,以便准确判定小物块所受摩擦力的方向; 第二,注意小物块与传送带共速前,小物块是否已经滑出传送带;若小物块还没有滑出传送带,则要依据小物块的受力情况确定小物块的运动情况,这是求解传送带问题的关键点; 第三,注意小物块与传送带共速后,如果是水平传送带,则小物块将随传送带做匀速直线运动;如果是倾斜传送带,则需要比较mgsinθ与μmgcosθ的大小关系,以便确定小物块所受摩擦力的方向; 第四,注意小物块在传送带上留下的痕迹问题,本质上是小物块与传送带间的相对运动的位移问题,但要特别注意是否存在在同一段传送带上出现二次(重复)摩擦的问题. 例1如图9所示,是长为L=16 m、倾角为37°的传送带,其转动速度为v=10 m/s.小物块与传送带间的动摩擦因数μ=0.5,在传送带顶端A处无初速度地释放一个质量为m=0.5 kg的小物块.已知sin 37°=0.6,cos 37°=0.8,g=10 m/s2.求: ①传送带顺时针转动时,小物块从顶端A滑到底端B的时间; ②传送带逆时针转动时,小物块从顶端A滑到底端B的时间. 图9 例1题图 分析①当传送带顺时针转动时,由于小物块受到的摩擦力沿传送带斜向上,小物块做匀加速运动,由牛顿第二定律得: mg(sin 37°-μcos 37°)=ma1 解得:a1=2 m/s2 ②当传送带逆时针转动时,由于小物块受到的摩擦力方向沿传送带斜向下,小物块做匀加速运动,由牛顿第二定律得: mg(sin 37°+μcos 37°)=ma2 解得:a2=10 m/s2 当小物块运动的速度与传送带的速度相等时,设经历的时间为t2,通过的位移为x2.由运动学公式得: 当小物块与传送带的速度相等时,由于mgsin 37°>μmgcos 37°,因此,小物块此后相对于传送带向下加速运动,受到的摩擦力方向变为沿传送带斜向上,由牛顿第二定律得: 接着,小物块做以加速度a3的匀加速运动,通过的位移为:x3=l-x2=11m 解得:t3=1s(t3=-11 s舍去) 所以t总=t2+t3=2 s. 点评求解小物块在传送带上运动的时间问题,务必注意弄清小物块相对传送带的运动方向,从而确定其所受摩擦力的方向,再利用牛顿第二定律求出加速度,由速度公式或者位移公式求出小物块的运动时间. 例2如图10所示,某传送带两端A、B间的距离L=4m,传送带倾角θ=37°,传送带以v=4 m/s的速度顺时针转动.现将质量为m=1 kg的小物块放在传送带的底端A点,小物块与传送带间的动摩擦因数为μ=0.5,g取10 m/s2,sin 37°=0.6,cos37°=0.8.小物块在一沿传送带向上的大小为F=6N的恒定拉力作用下,使其由静止开始沿传送带向上运动,当小物块的速度与传送带速度相等时,撤去拉力,则当滑块到达传送带顶端时,滑块速度为多大? 图10 例2题图 分析开始时,小物块受到重力、弹力、摩擦力和拉力等4个力的作用,由牛顿第二定律得:F-mgsin 37°+μmgcos 37°=ma1 解得:a1=4 m/s2 由速度公式:v=a1t1,得t1=v/a1=1.0s 在此过程中,小物块通过的位移为: 撤去拉力后,由于mgsin 37°>μmgcos 37°,小物块做匀减速运动,由牛顿第二定律得: mgsin 37°-μmgcos 37°=ma2 解得:a2=2 m/s2 点评求解小物块的速度问题,关键是弄清小物块在传送带上的受力情况和运动情况,由牛顿第二定律求出小物块的加速度,再结合运动学公式求小物块的速度. 例3一水平传送带装置如图11所示.传送带的左、右两个端点为A、B,AB长L=2 m,开始时,传送带处于静止状态.当质量m=2 kg的煤块(可视为质点)轻放在传送带A点时,传送带立即启动,启动过程可视为加速度a=2 m/s2的匀加速运动,加速结束后传送带立即匀速运动.已知煤块与传送带间动摩擦因数μ=0.1,设最大静摩擦力等于滑动摩擦力(g取10 m/s2).为了使煤块在最短时间内通过传送带,则: 图11 例3题图 ①传送带至少加速多长时间? ②在此种情况下,煤块从A点运动到B点的过程中在传送带上留下的痕迹多长? 分析①为了使煤块在最短时间内通过传送带,则必须让煤块一直做加速运动.煤块在传送带上的加速度为:μmg=ma1,即:a1=μg=1.0 m/s2 煤块从A点运动到B点的速度为: 显然,传送带必须加速到2 m/s,则加速的时间为:t1=v/a=1 s ②煤块从A点运动到B点的时间为: 传送带在加速过程中通过的路程为: 传送带在匀速过程中通过的路程为: x2=vt2=2 m 则煤块从A点运动到B点的过程中在传送带上留下的痕迹长度为: s相=x1+x2-L=1 m 例4如图12所示,某煤矿有一传送带与水平地面间的夹角θ=37°,传送带以v=10 m/s的速率逆时针转动.在传送带上端A点静止释放一个质量为m=1.0 g的黑色煤块,经过2 s运动到传送带下端B点并离开传送带,煤块在传送带上留下一段黑色痕迹.已知煤块与传送带之间的动摩擦因数μ=0.5,sin37°=0.6,g=10 m/s2,求: ①传送带从A到B的长度; ②煤块从A运动到B的过程中传送带上形成痕迹的长度. 图12 例4题图 分析①开始时,煤块在重力、弹力和摩擦力的作用下做匀加速运动,由牛顿第二定律得: mgsinθ+μmgcosθ=ma1 解得:a1=10 m/s2, 由速度公式求得煤块速度达到v=10 m/s的时间:t1=v/a1=1 s 接着,摩擦力方向发生突变,由斜向下变为斜向上,由牛顿第二定律得:mgsinθ-μmgcosθ=ma2 解得:a2=2 m/s2 煤块在第2 s内通过的位移为: 可见,传送带AB间的长度为: L=x1+x2=16 m ②煤块速度小于传送带时有: s相1=vt1-x1=5 m 煤块速度大于传送带时有:s相2=x2-vt2=1 m 由于s相1>s相2,由此可知,煤块在传送带上运动的过程中,在传送带上留下的痕迹长为5 m. 点评痕迹问题本质上是两者发生相对运动的问题.例3中的煤块的速度始终小于传送带,而例4中的煤块,开始时煤块速度小,后来煤块速度大,有重复摩擦的部分,因此,在求解痕迹问题时,必须弄清有没有重复摩擦的部分. 例5随着电子商务的迅速发展,对物流的需求急剧增加,如图13所示是物流运输过程中卸货的传送装置示意图,水平部分AB和倾斜部分BC的长度均为2m,BC部分与水平面之间的夹角θ=37°.传送带以v=1 m/s的速度沿顺时针方向匀速运转,把包裹轻放到水平传送带A端,包裹经过B端前后速度大小不变且不脱离传送带.已知包裹与传送带间的动摩擦因数为0.5,包裹放上后传送带速度不变.取重力加速度g=10 m/s2,sin37°=0.6,cos37°=0.8.求: ①包裹到达B端时的速度大小; ②包裹从A端传送到C端所需时间. 图13 例5题图 分析①包裹开始时做匀加速运动,由牛顿第二定律得:a1=μg=5.0 m/s2 当包裹的速度达到v=1 m/s时,通过的位移为: 可见,包裹的速度达到v=1 m/s后做匀速运动,到达B端时的速度为v=1 m/s. ②包裹在水平传送带上加速时间为: t1=v/a1=0.2 s 包裹在水平传送带上匀速运动时间为: t2=(L-x1)/v=(2-0.1)/1=1.9 s 包裹在倾斜传送带上运动时,一直做匀加速运动,由牛顿第二定律得:mgsinθ-μmgcosθ=ma2 解得:a2=2.0 m/s2 可求得包裹在倾斜传送带上的运动时间为:t3=1.0 s 可见,包裹从A端传送到C端所需时间为:t=t1+t2+t3=3.1 s 点评:对于组合传送带问题,关键在于弄清小物块从一个传送带转到第二个传送带上时,其受力情况、速度等的变化情况. 例6如图14所示,倾斜放置的传送带A、B两端长为L=0.8 m,传送带与水平面间的夹角为θ=37°,以v0=1 m/s的速度沿顺时针方向匀速转动,传送带底端B处与放在光滑水平地面上的平板小车平滑连接(可认为物体经过该连接处速率不变).一小物块(可视为质点)从传送带顶端A处由静止释放,一段时间以后,小物块到达传送带底端B处,随后滑上平板小车的上表面.小物块的质量m=1 kg,与传送带之间的动摩擦因数为μ1=0.5,与平板小车上表面之间的动摩擦因数为μ2=0.4;平板小车质量M=2 kg.最大静摩擦力等于滑动摩擦力,重力加速度g取g=10 m/s2,sin37°=0.6,cos37°=0.8,求: 图14 例6题图 ①小物块运动到传送带底端B处的速度大小以及小物块在传送带上运动的时间; ②为保证小物块不会从平板小车上表面滑出,平板小车的长度l应满足怎样的条件? 分析①小物块从传送带上刚滑下时,由牛顿第二定律得:mgsinθ+μ1mgcosθ=ma1 解得:a1=10 m/s2 小物块达到与传送带共速的时间为: t1=v0/a1=0.1 s 小物块在t1时间内通过的位移为: 小物块与传送带共速后,由于摩擦力发生突变,则其加速度将发生变化,由牛顿第二定律得:mgsinθ-μ1mgcosθ=ma2 代入数据解得:a2=2 m/s2 解得:vB=2 m/s 小物块从共速到传送带B端的运动时间为: t2=(vB-v0)/a2=0.5 s 则小物块在传送带上的运动时间为: t=t1+t2=0.6 s ②小物块滑上平板小车上后,由于摩擦力的作用,小物块开始做匀减速运动,平板小车做匀加速运动. 对小物块有:μ2mg=ma3,解得:a3=4 m/s2 对平板小车有:μ2mg=Ma4,解得:a4=2 m/s2 设小物块滑上平板小车后经时间t4与平板小车的速度相等,共速为v共,小物块的位移为x2,平板小车的位移为x3,由运动学公式得: v共=v-a3t4=a4t4 平板小车的最小长度满足:Lmin=x2-x3 点评求解传送带与板块相结合的综合问题,不仅要掌握传送带和板块问题的基本解题方法,并且要注意小物块从一种模型过渡到第二种模型时,其受力情况、运动情况的变化特点,同时,还要注意衔接处变化特征. 总之,有效求解传送带问题,务必注意三点:其一,要正确理解传送带问题的特点;其二,要准确分析小物块与传送带共速时,小物块所受摩擦力的突变情况;其三,要熟练应用相关的牛顿第二定律和运动学公式.
2.2 倾斜传送带



3 解题思路

4 注意事项
5 典例剖析
5.1 求小物块在传送带上的运动时间

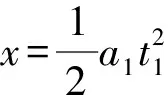

5.2 求小物块离开传送带时的速度


5.3 求小物块在传送带上留下的痕迹长度



5.4 求解组合传送带问题


5.5 求解传送带与板块综合问题


6 结束语

