一道2022年联赛试题的探究及在高考中的应用

王东海

(安徽省合肥市肥东县城关中学,安徽 合肥 231600)

直线与圆锥曲线的位置关系问题一直是高考及联赛的热点和难点,颇受命题者的青睐.在这类考题的命题中往往都是探求一些特殊结论,这些结论看似特殊,实则往往都具有普遍性.我们在解答考题后要深入拓展到一般情况,还要注意探寻其他圆锥曲线的对偶性质.下面以2022年四川数学联赛一道圆锥曲线试题的探究为例进行说明.

1 真题呈现

题目(2022年四川预赛第9题)如图1所示,ABCD是一个矩形,AB=8,BC=4,M,N分别为AB,CD的中点,以某动直线l为折痕将矩形在其下方的部分翻折,使得每次翻折后点M都落在边CD上,记为点M′,过点M′作M′P垂直于CD交直线l于点P.设点P的轨迹是曲线E.

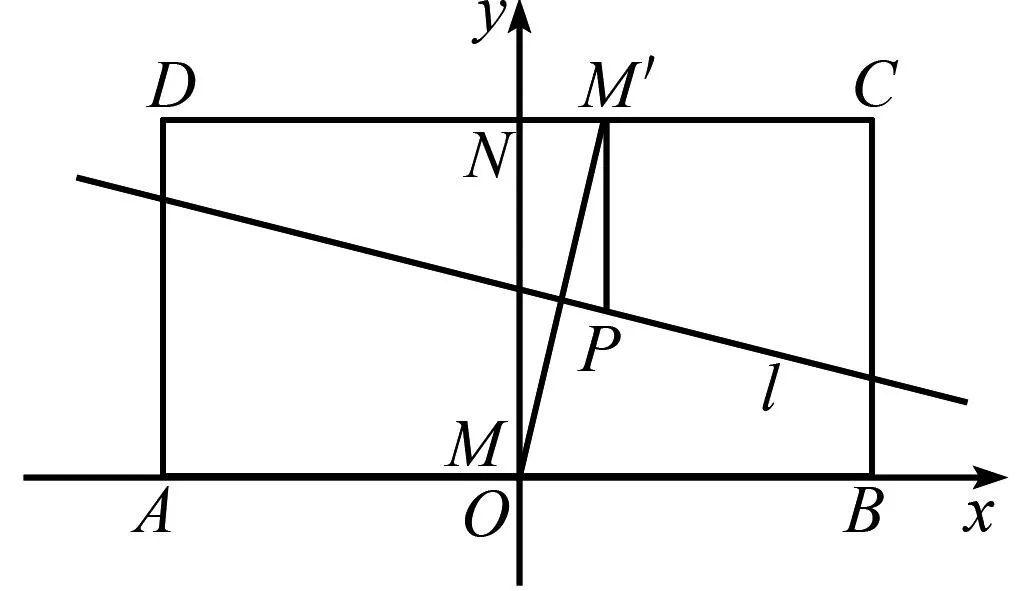
图1 2022年四川预赛第9题图

(1)建立恰当的直角坐标系,求曲线E的方程;

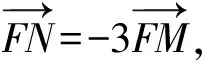
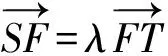
2 解法探究

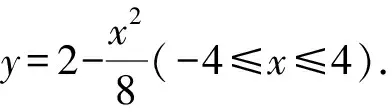
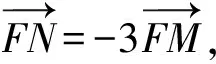
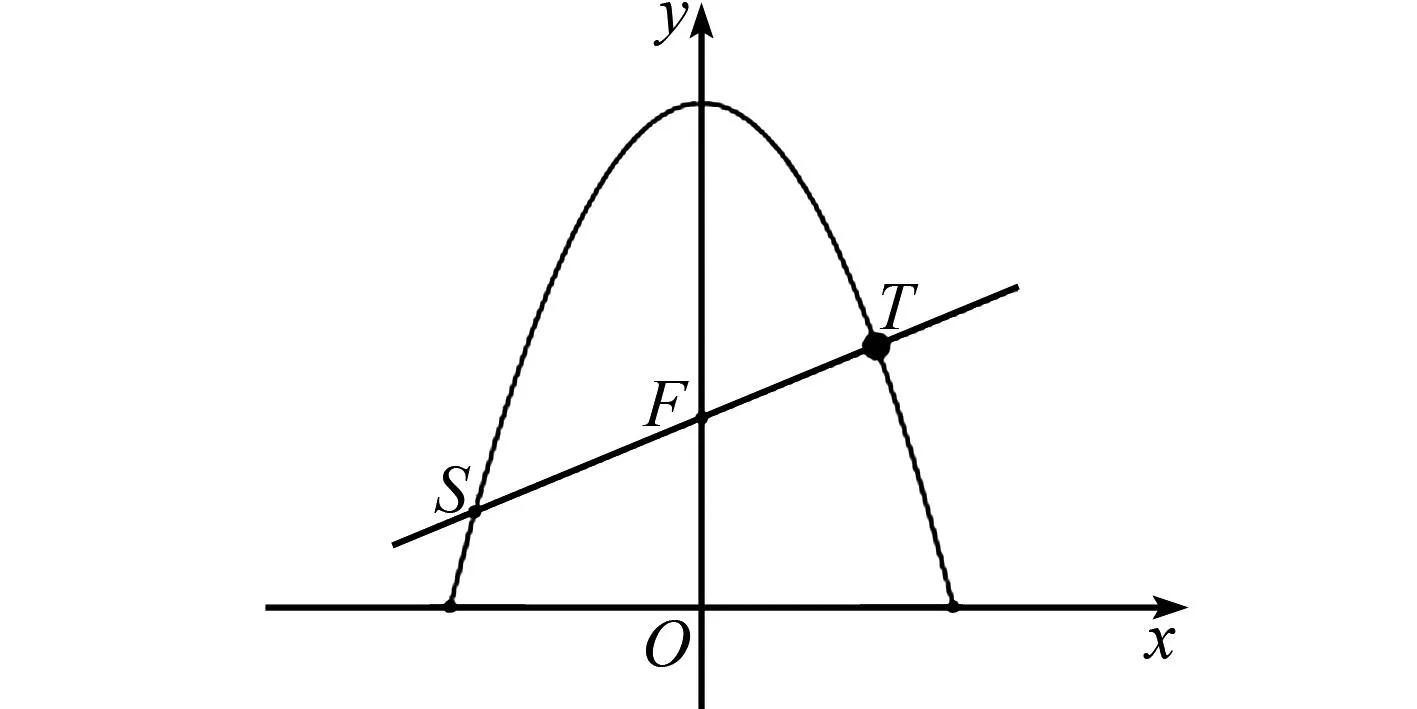
图2 第(2)小问几何图

消元,得x2+8kx-8=0.

①

由韦达定理知x1+x2=-8k,x1x2=-8.

②

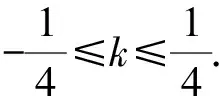
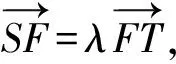
(-x1,1-y1)=λ(x2,y2-1).

所以x1=-λx2.

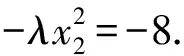
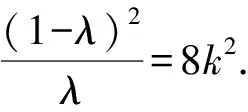
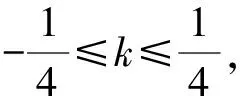
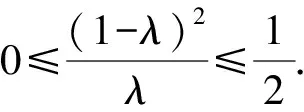
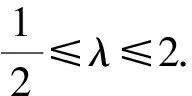
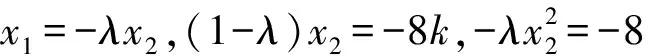
解法2 (点参法)设两个交点为S(x1,y1),T(x2,y2),因为S,T在抛物线上,有

③

④

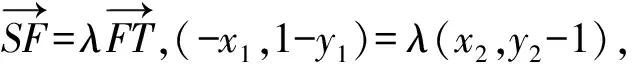
x1=-λx2,y1-1=-λ(y2-1).

将此式代入③,得

再将④式代入,得

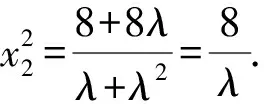
又根据题意知-4≤x2≤4,且由

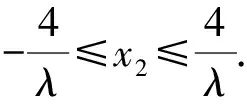
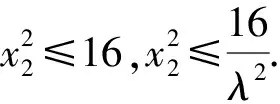
评注首先设出点坐标,然后推出含有五个未知数x1,y1,x2,y2,λ的四个方程,再通过消元处理可以得到x2与λ的一个等式.最后由点T的横坐标x2的范围来确定λ的取值范围.

解法3 (定比点差法)设两个交点为S(x1,y1),T(x2,y2),因为S,T两点在抛物线上,有

③

④

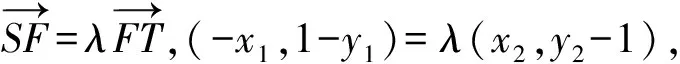
x1=-λx2,y1-1=-λ(y2-1).

④×λ2-③,得

从而λ2y2=1-λ(y2-1)+2λ2-2.

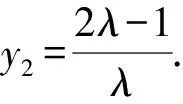
而由题意知0≤y2<2,

⑤

且由0≤y1<2,0≤1-λ(y2-1)<2,

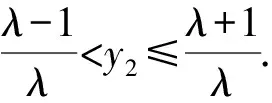
⑥

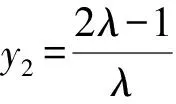
评注先利用定比点差法确定出坐标y2与λ的等量关系,再由坐标y2的范围定出λ的范围.使用定比点差法的关键在于根据方程特点先配比好系数然后作差,相比解法2运算量少一些.

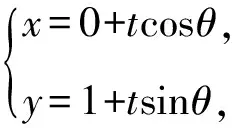
代入抛物线方程,得

整理,得cos2θ·t2+8sinθ·t-8=0.

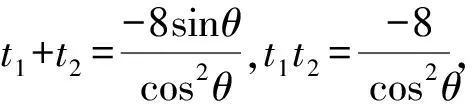
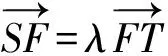
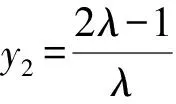
评注对于分点弦这类问题,使用直线的参数方程是常用方法.这是因为t的几何意义恰能方便表示线段之比问题,但准确理解直线的参数方程中参数的几何意义是解题的基础.

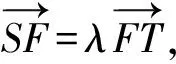
由抛物线参数方程可设T(8t,2-8t2),则得点S(-8λt,1-λ(1-8t2)),

将点S代入抛物线方程,可得

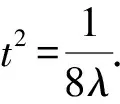
⑦

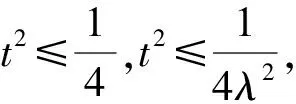
评注利用抛物线参数方程实际上还是先确定t和λ的等量关系,再由坐标t的范围确定λ的范围.

3 推广探究

美籍匈牙利数学家波利亚曾说:“没有任何一个题目是彻底完成了的,总还会有些事情可以做.”细品解题过程,笔者发现第(2)问的解答值得探究,笔者思考,对于一般性的抛物线有无一个统一的结论呢?需不需要也截取抛物线的一段呢?如果背景的圆锥曲线换成椭圆、双曲线,是否仍有类似的结论呢[1]?基于以上思考,笔者探究得到如下结论:

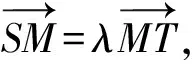
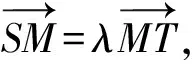
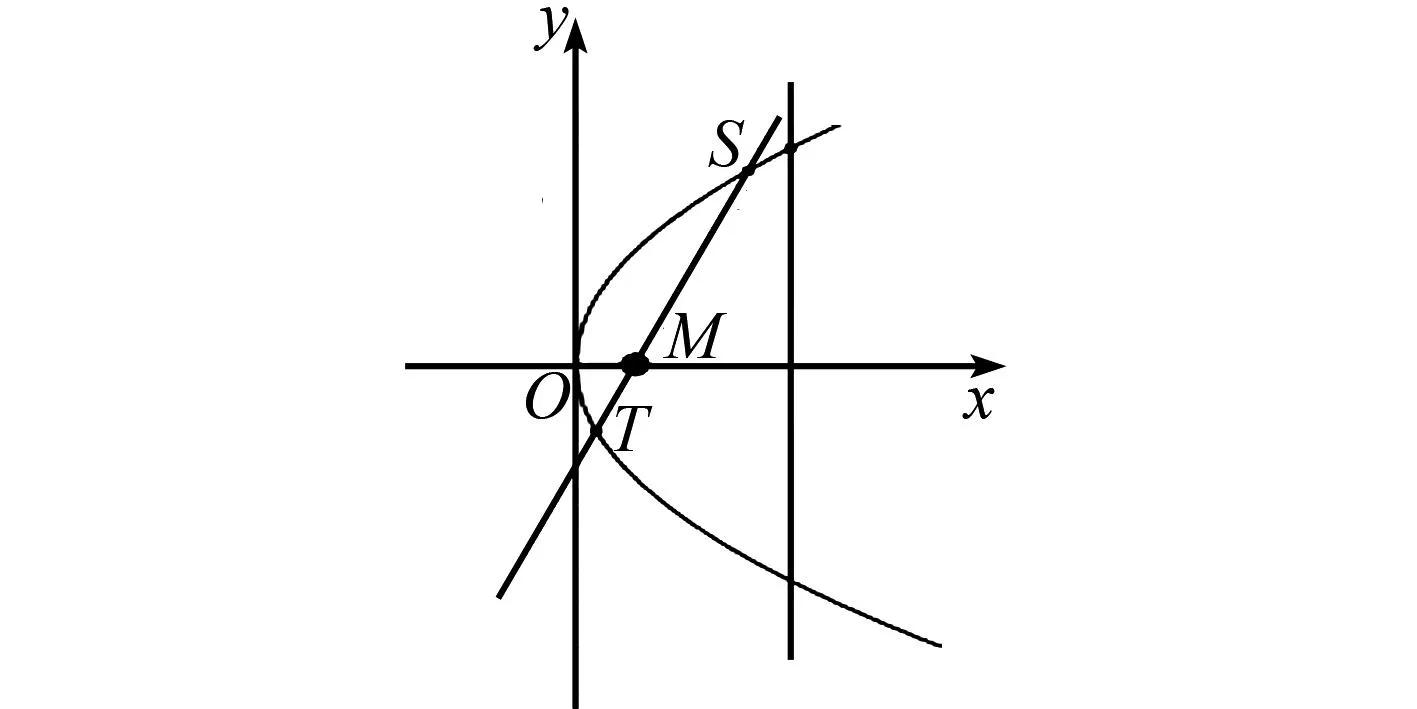
图3 结论1几何图

从而得m-x1=λ(x2-m),-y1=λy2.

所以x1=m-λ(x2-m),

⑧

y1=-λy2.

⑨

又S,T两点在抛物线上,代入,得

⑩

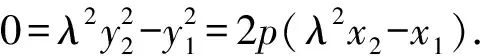
所以λ2x2-x1=0=λ2x2-m+λ(x2-m).

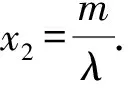
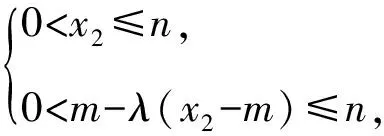
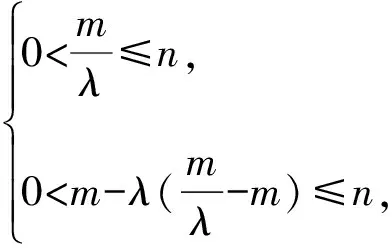
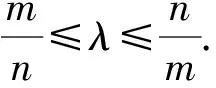
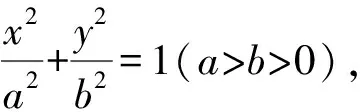
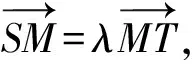
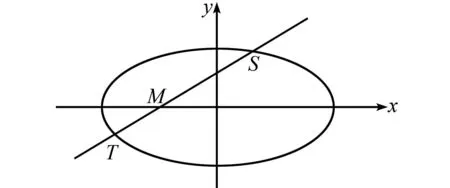
图4 结论2几何图

所以m-x1=λ(x2-m),-y1=λy2.

所以x1=m-λ(x2-m),

⑧

y1=-λy2.

⑨

又S,T两点在椭圆上,代入,得

则(x2λ-m-λm+λx2)(x2λ+m+λm-λx2)=(λ2-1)a2.

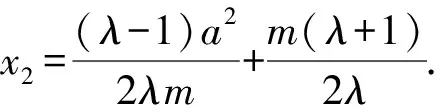
而由题意知-a≤x2≤a.

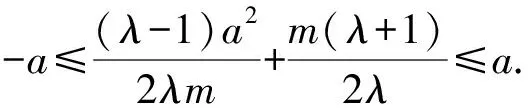
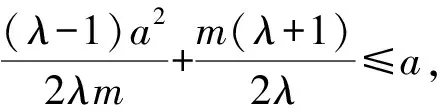
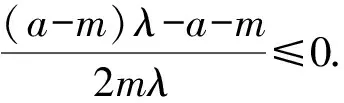
即2mλ[(a-m)λ-a-m]≤0.

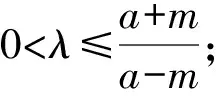
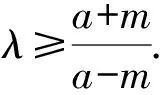
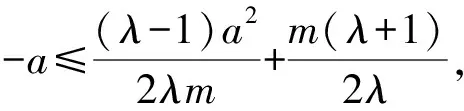
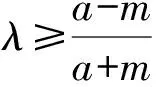
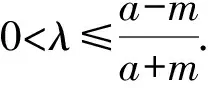
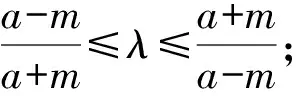
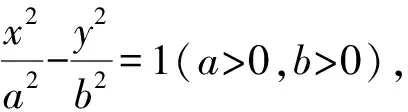
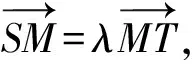
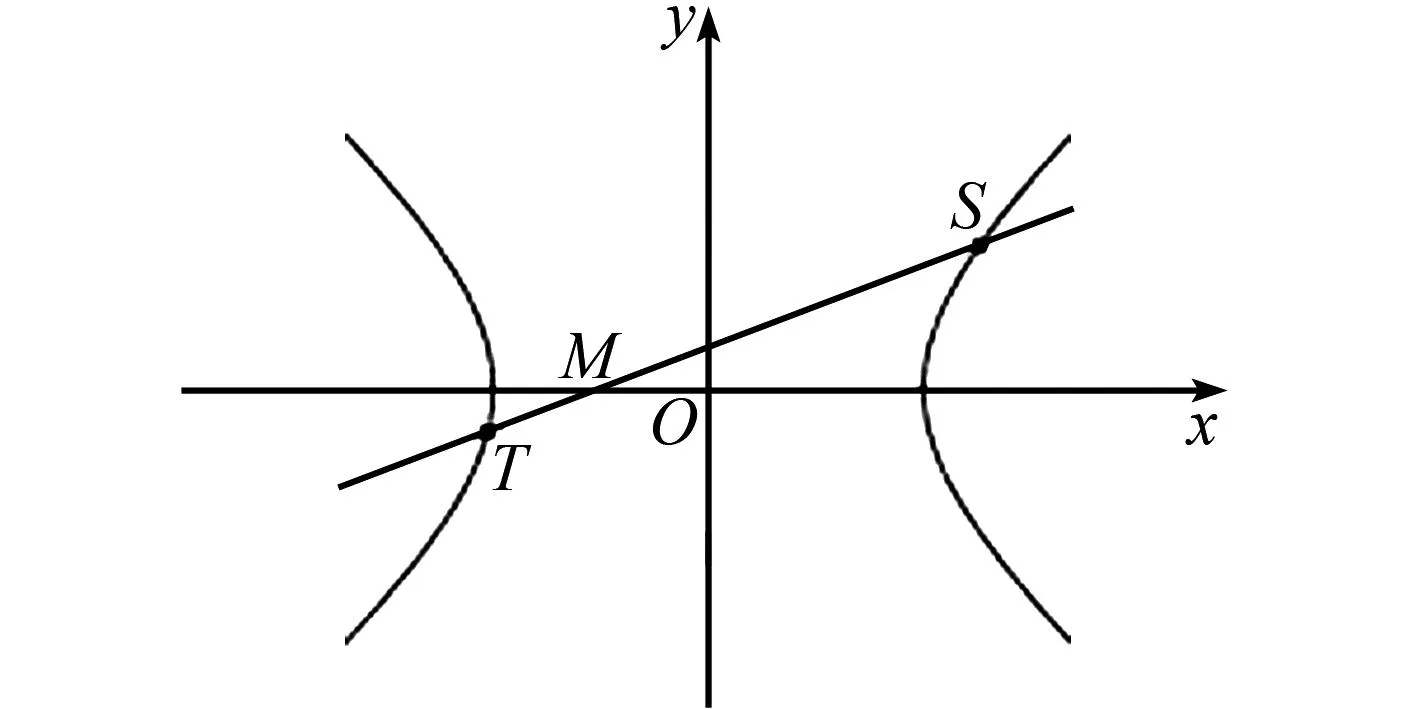
图5 结论3几何图

所以m-x1=λ(x2-m),-y1=λy2.

所以x1=m-λ(x2-m),

⑧

y1=-λy2.

⑨

又S,T两点在双曲线上,则有

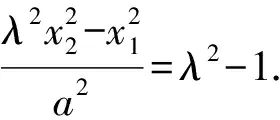
将⑧代入上式,得

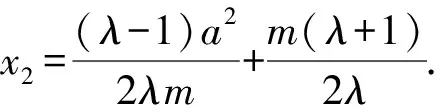
而由题意知x2≤-a,

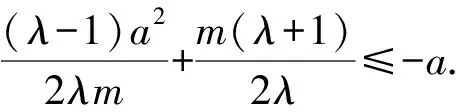
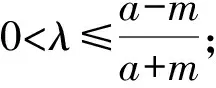
4 变式探究

此道四川联赛试题,如果我们将题中λ变为常数,而将定点F改为x轴上一个动点(λ,0),那么此动点的横坐标λ的取值范围又是怎样的呢?

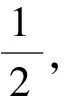
(1)求椭圆Γ的方程;

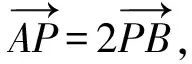
解析(1)易得椭圆Γ:x2+4y2=1.

(2)设A(x1,y1),B(x2,y2),A,B在椭圆上,故

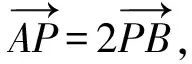
又λ=0不合题意,将式代入,得

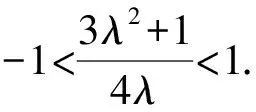
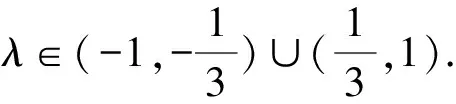
我们根据这道变式题,也可以把它推广到一般情形 :

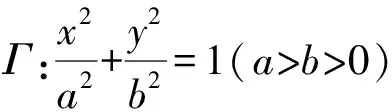
证明方法类似于结论2的定比点差法,略.

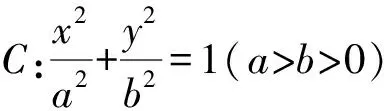
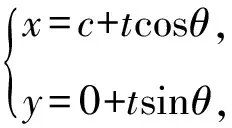
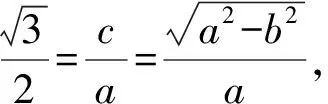
将直线AB参数方程代入椭圆方程x2+4y2=4b2,得(c+tcosθ)2+4t2sin2θ-4b2=0.

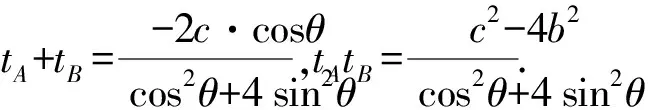
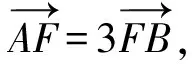
将其代入上式,得

化简此式可得tan2θ=2.

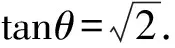
根据这道变式题,可以把它推广到一般情形:

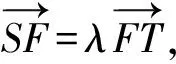
5 结论应用

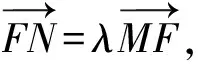
解析设l的纵截距为b,则e=1,k=-b.

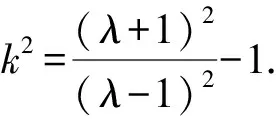
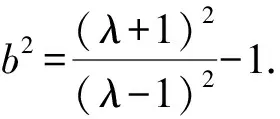
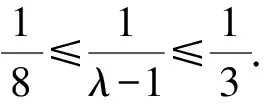
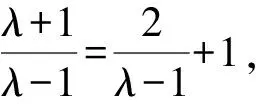
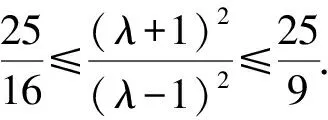
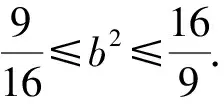
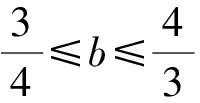
6 结束语

在数学教学中,我们不能满足于将问题解决了就万事大吉,而是要进一步进行探究.我们可以进行解法探究,也可以将问题一般化进行拓展研究,还可以进行变式研究.在教学中,教师要为学生提供探究的机会,让学生在探究中体会到学习的快乐,让探究成为一种习惯.