微元法证明均匀球壳对壳内质点的万有引力为零

段石峰

(长沙市周南中学,湖南 长沙 410201)

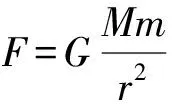
质量分布均匀的球壳具有球对称性(绕球心任意旋转都是相同的),球壳对壳内外质点的万有引力都可以用微积分或高斯定理求解[2],而球体是一层层同心球壳的叠加,因此只要解决球壳的问题,那么相关的一系列问题都迎刃而解.其中有一个很重要的结论:均匀球壳对壳内质点的万有引力为零.这个结论还可以借助空间“立体角”的概念进行证明,但这些方法都属于高等数学.高中物理通常把这个结论不加证明地告诉学生,尽管不碍于问题的解决,却难免有“强行灌输”之嫌,终究给学生留下“知其然而不知其所以然”的疑惑和缺憾,这不利于学生思维能力的发展.

虽然高中阶段对微积分不作要求,但由它派生出来的微元法属于初等方法,并且非常巧妙地实现了降解.微元法是高中物理处理问题的重要方法,基本思路是“先无限分割,再累积求和”,即先把物体分割成足够小的质量微元,求出它们之间的万有引力,再求力的矢量和就可得到物体之间的万有引力.本文利用微元法从两种不同的视角,证明均匀球壳对壳内质点的万有引力为零.

1 用微元法处理的基本思路

当物体不能看作质点时,物体之间的万有引力如何计算?基本思路是将物体进行分割,当分割得足够细时,每一部分都可以看作质点[3].如图1所示,首先把A、B两个物体分割成很多小块,每一小块的体积都很小,可以看作质量为Δm的质点,A、B物体上任意两个质点间的万有引力为

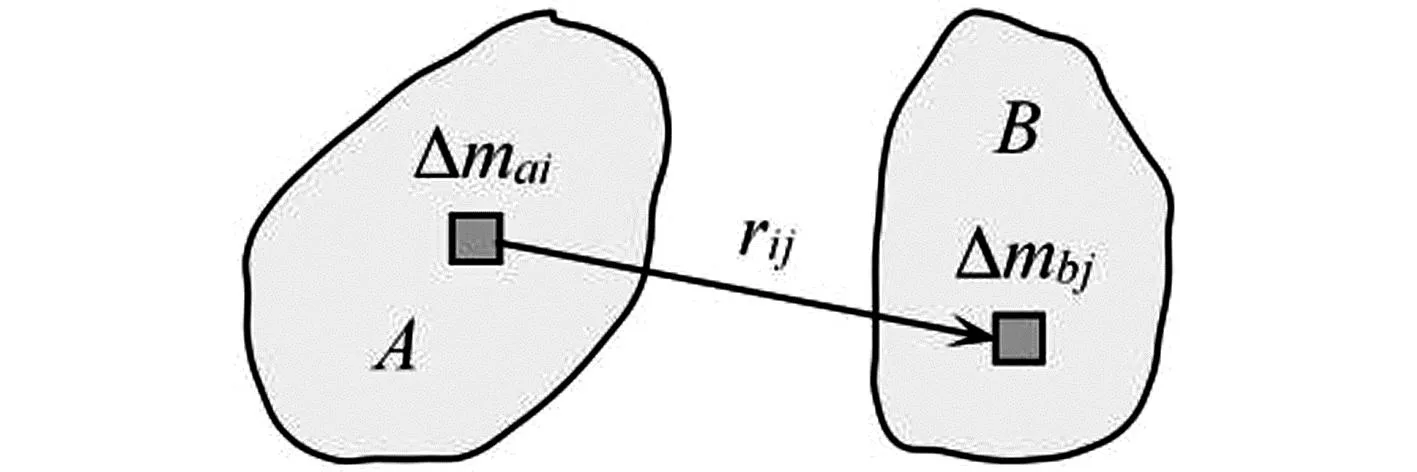
图1 微元法基本思路

然后求出B物体上所有质点对Δmai的万有引力,将这些力进行矢量求和,得到B对A上任意质点Δmai的万有引力为

最后把B对A上每一个质点的万有引力进行矢量求和,得到A、B两物体之间的万有引力为

即A、B之间的万有引力等于A的每一部分与B的每一部分的万有引力的矢量和.然而对于体积不规则的物体,求和过程很难计算;对于具有对称性的物体,可以利用对称性简化求和过程.

2 用微元法证明的两种视角

2.1 视角一:用圆锥截取

如图2所示,质量为m的质点处在球壳内的任意位置P点,过P点任意作一条直线与球壳的交点为A点和B点.以P点为顶点、以直线AB为对称轴任意作一对顶角很小的圆锥,圆锥在球壳上截取两个面积很小的球面,可以看作以A点和B点为圆心的圆平面,圆的面积分别为S1和S2.

图2 用圆锥截取的球面示意图

设球壳单位面积的质量为σ,截取的两个质量微元m1和m2可以看作位于A点和B点的质点,它们到P点的距离分别为r1和r2,对P点处质点m的万有引力方向相反,大小分别为

分别过A点和B点作垂直于AB的圆锥底面圆,半径分别为R1和R2,面积分别为S1′和S2′.设∠OAB=∠OBA=θ,则圆面S1与S1′的夹角为θ,圆面S2与S2′的夹角也为θ,它们的关系为

由于垂直于AB的两个圆锥底面圆相互平行,所以存在相似三角形关系,由对应边成比例可得

联立以上各式可得F1=F2,即F1和F2的矢量和为零.现将对顶圆锥绕P点旋转,所截取的每一对质量微元对P点处质点的万有引力的矢量和都为零,并且可以截取到整个球壳,所以整个球壳对P点处质点的万有引力为零,于是证明了均匀球壳对壳内任意位置质点的万有引力为零[4].

2.2 视角二:用环带分割

如图3所示,质量为m的质点处在球壳内的任意位置P点,以P点为顶点、以过P点的直径为对称轴任意作一对圆锥,圆锥母线与对称轴的夹角为θ,此角增大Δθ(Δθ→0)的过程中,圆锥在球壳上扫出两条环带,两环带到P点的距离分别为r1和r2,宽度分别为r1Δθ和r2Δθ,半径分别为R1和R2,则两环带的面积分别为

S1=2πR1·r1Δθ,S2=2πR2·r2Δθ

图3 用环带分割示意图

设球壳单位面积的质量为σ,则两环带的质量分别为

m1=σS1,m2=σS2

将两环带再分割为质量微元Δm1和Δm2,对P点处质点m的万有引力方向具有对称性,与对称轴的夹角为θ,大小分别为

那么两环带对P点处质点m的万有引力方向沿对称轴相反,大小分别为

由于两环带所在的圆平面相互平行,所以存在相似三角形关系,由对应边成比例可得

3 结束语

从证明的过程来看,之所以分割的每一对质量微元对球壳内任意质点的万有引力为零,是因为万有引力具有一个很明显的特点,那就是它与距离的平方成反比.换句话说,“均匀球壳对壳内质点的万有引力为零”这个结论并非偶然,而是平方反比规律的必然结果.既然如此,由于库仑定律同样遵循平方反比规律,那么本文的证明方法和结论也同样适用于库仑力,即“电荷分布均匀的球壳对壳内任意位置点电荷的库仑力为零”.只不过带电体产生的静电场容易与物质发生相互作用,引起明显的静电感应现象或电介质极化现象,导致电荷的分布难以保证具有球对称性.