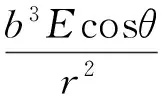点电荷和介质球壳系统的电势分布
王树平 范 虹
(河北建筑工程学院数理系,河北 张家口 075000)
点电荷和介质球壳系统的电势分布
王树平 范 虹
(河北建筑工程学院数理系,河北 张家口 075000)
通过求解拉普拉斯方程与泊松方程,得到了点电荷和介质球壳系统的电势分布表达式,并对结果进行讨论,得出了若干有意义的结论.
点电荷;介质球壳;电势;分离变量法
文献[3]、[4]分别计算了点电荷与介质球、均匀外电场中有介质球壳系统的电势分布.本文通过对点电荷和介质球壳系统的电势的计算和讨论将阐明:上述两种情形的电势分布都可由点电荷和介质球壳系统的电势分布给出.
1 计 算

设有介电系数为ε的介质球壳,置于空气中.介质球壳的内、外半径分别为a和b,在距离介质球壳的球心为r0处有一点电荷(假设r0>b,见图1),其带电量为q,计算空间的电势分布[1].
显然,球壳内(r
2φ1=0 (r (1) (2) (3) 由于点电荷的作用,介质球壳产生极化,球壳内(r φ1(r,θ)=φq1+φp1(r,θ) (r (4) φ2(r,θ)=φq2+φp2(r,θ) (a≤r≤b) (5) φ3(r,θ)=φq3+φp3(r,θ) (r>b) (6) 边界条件为 φ1=有限值 (r=0) (7) 已知点电荷在球壳内、中、外三区域产生的电势分别为 (11) (12) (13) 应用分离变量法,并结合式(7)、式(8)给出的条件,可设极化电荷在球壳内、中、外产生的电势分别为 (14) (15) (16) 于是得到球壳内、中、外的电势表达式分别为 (17) (18) (19) (20) 由式(9)、式(10)及式(17)-(20)得到 由式(21)解得 (22) (23) (24) (n=0,1,2,…) (25) 以上三式中 k′=b2n+1[εn+ε0(n+1)][ε0n+ε(n+1)]-a2n+1n(n+1)(ε-ε0)2 k″=n(ε-ε0)a2n+1+[ε0n+ε(n+1)]b2n+1 将式(22)-(25)分别代入式(17)、式(18)、式(19),得到介质球壳内、中、外的电势分布分别为 在式(27)中,令a=0,b=R,马上能得到点电荷和介质球系统的电势分布 在介质球内的电势表达式为 (n=0,1,2,…)(r≤R) (29) 在介质球外的电势表达式为 (30) 这与文献[3]的结论完全相同. 众所周知,在ε→∞的条件下,介电系数为ε的介质相当于导体,利用式(26)-(28)及ε→∞的条件,很容易得到点电荷与导体球壳系统的电势分布. 导体球壳内的电势为 φ1=0 (n=0,1,2,…)(r (31) 导体球中的电势为 φ2=0 (n=0,1,2,…) (a≤r≤b) (32) 导体球外的电势为 (33) 若点电荷q(<0)沿z轴正向趋于无穷远,同时q值也趋于无穷大,但保证q在讨论的范围内所激发的电场为非零有限场值,则此时q在讨论的范围内所激发的电场是沿z轴正向的均匀的电场,其大小为: (34) 式(34)中负号的引入是因为q<0,这里要求场强大小E非零有限. 根据式(20),式(26)可改写为 再由式(34)知,此时式(35)中的求和只有当n=0,1时不为零,其余都为零.另外式(35)中是取无穷远为电势零点的,若均匀电场占据整个空间时,不能再取无穷远为电势零点.当电势零点改变时,电势的表达式应加一常量U0[2],则均匀场中有介质球壳情形的壳内的电势为 (36) (37) 同理,式(27)可改写为 由式(34)知,当q(r0)→∞时,式(38)中的求和也只有当n=0,1时不为零,其余都为零.则均匀场中有介质球壳情形的球壳中的电势为 与上相同,仍取z=0的平面电势为零,由式(34)、式(39)可得到球壳中的电势为 (a≤r≤b) (40) 同理,式(28)可改写为 (n=0,1,2,…) (r>b) (41) 再由式(34)知,式(41)中的求和只有当n=0,1时不为零,其余都为零.则均匀场中有介质球壳情形的壳外的电势为 (n=0,1,2,…) (r>b) (42) 与上相同,仍取z=0的平面电势为零,由式(34)、式(42)可得到给出球壳外的电势为 (43) 式(37)、式(40)、式(43)给出的电势分布与文献[4]的结论完全相同. 当εr=ε/ε0→∞时,介质球壳可看成导体球壳,由式(37)、式(40)、式(43)知处于均匀外电场中的导体球壳的内、中、外的电势分别为 φ1=0 (r (44) φ2=0 (a≤r≤b) (45) (46) 综上所述,点电荷与介质球、点电荷与导体球壳、均匀外电场中有介质球壳、均匀外电场中有导体球壳系统的电势分布,都可由点电荷和介质球壳系统的电势给出.因此对点电荷和介质球壳系统的电势的计算具有普遍意义. [1]王竹溪,郭敦仁.特殊函数概论[M].北京:科学出版社,1965.240 [2]封小超.关于电势零点选择的几个问题[J].大学物理,1986.5(7):13 [3]李子军,李根全,白旭芳.点电荷与介质球系统电势的计算和讨论[J].大学物理,2003,9(5):11 [4]倪忠楚,邱荒逸.均匀外场中介质球壳的场分布[J].大学物理2006,25(4):5 TheElectricPotentialDistributionofPointChargeandDielectricSphereShellSystem WANGShu-ping,FANHong (Hebei Institute of Architecture and Civil Engineering,Zhangjiakou,075000) The electric potential distribution of point charge and dielectric sphere shell system is calculated by using the separation variable method,and someuseful calculations are presented as well. point charge;medium shell;electric potential;method of images 2016-12-08 王树平(1977-),男,副教授,张家口,075000 10.3969/j.issn.1008-4185.2017.03.028 O441.4 A







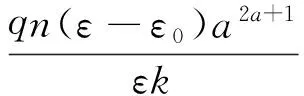


2 讨 论
2.1 点电荷与介质球系统的电势分布


2.2 点电荷与导体球壳系统的电势分布
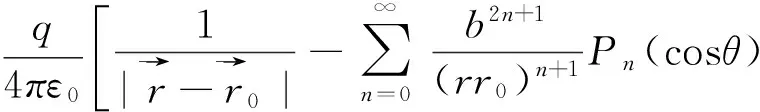
2.3 均匀外电场中介质球壳的电势分布
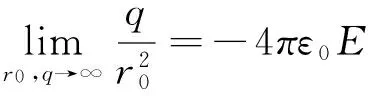



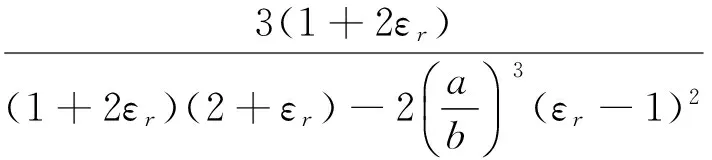


2.4 均匀外电场中导体球壳的电势分布