空间分布系列球壳声场耦合与辐射特性研究

李 凯，俞白兮，俞孟萨，3，白振国，3

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082；3.船舶振动噪声重点实验室，江苏无锡 214082）

0 引 言

耐压壳体是水下载人平台的核心结构，常见形式主要有圆柱壳、球壳、椭球壳等简单壳体。工作深度超过1000 m 的大深度载人潜水器则多数采用球壳结构[1]，以球壳为基本单元，又发展了多球壳组合结构[2]。日本Shinkai HU06 载人潜水器采用双球壳结构，球壳之间设置圆柱形连接通道；俄罗斯10831 型深海作业核动力潜艇采用多个球壳串联的组合结构；美国的Mystic 和Avalon 深潜救生艇（DSRV）则采用了多球交接结构[3]；此外，Ross[4]还提出了一种外部圆环壳+内部多球壳的分布式水下空间站概念方案。

多壳体组合结构由数个相对独立的耐压壳体按照特定布局形式组合连接而成，各单体之间除了存在连接结构引起的机械相互作用外，还存在着单体辐射声波在声介质中的声场相互作用。白振国[5-6]通过引入柱函数加法公式建立了三个并排无限长弹性圆柱壳振动与辐射和散射声场耦合模型，结果表明三壳体间的声场耦合对系统的共振特征和声场分布特性都有显著影响，不同圆柱壳之间还存在着一定的声辐射遮蔽效应。同样，球壳间声场耦合效应对多球壳组合结构耦合声振特性的影响也不容忽视。因此，在不考虑连接结构机械相互作用的情况下，突出多球壳之间的声场相互作用，研究空间离散分布系列球壳的声场耦合与辐射特性，有利于掌握多球壳结构声学特征，为采用多球壳组合结构的大深度载人潜器声学设计提供基本依据。

多球耦合声场问题求解的关键是将各个球体的辐射声场统一表述到同一个球坐标系下，以便在每个球体表面应用振动-声耦合边界条件，这通常需要借助球函数加法定理来加以实现。New[7]运用球函数加法定理推导了双球体声辐射及多重散射解，并分析了两个脉动球体的散射声场相互作用对近场和远场声压及声辐射阻抗的影响。Thompson[8]研究了邻近球形散射体对球形声源辐射声场的影响，并进一步研究了两个球形声源之间的声场耦合作用[9-11]。针对非轴对称声场问题，Lease[12-13]引入了一般形式的球函数平移加法定理，求解了球形声介质中任意分布双球源系统的声辐射问题。这些研究均假设结构表面具有给定的振动速度分布，没有考虑声介质对结构振动的耦合作用。Huang[14]采用弯曲理论表征球壳振动，研究了平面波入射下双球壳系统声弹性耦合效应对散射声场的作用，将已知双球壳振动的声散射扩展到双弹性壳体的声散射问题。针对多球耦合声场问题，吴九汇[15]利用格林函数的双中心球坐标展开式推导了一类球函数加法公式，用于求解多球体系统声学散射问题。范威[16-17]推导了理想波导和楔形波导中球体散射声场的镜像解析解。赵开琦[18]则建立了理想界面附近点力激励下球壳振动声辐射的解析模型，他们在研究中应用球函数加法定理，考虑了界面反射的等效虚源对球壳散射或辐射声场的影响，这种多球系统声场耦合模型适用于沿对称轴线串列分布的多球壳声辐射和声散射计算。针对空间任意分布的多球壳阵列，张超[19]采用有限元+边界元方法计算了散射声场特性，并基于单个球壳的散射声场采用叠加法近似计算散射声场，经比较，确认球壳间互散射对多球壳散射声场有明显作用，不可忽略。赵腾瑞[20]进一步考虑了球壳间连接结构的作用，将球壳近似为刚性球体，比较了弹性连接和刚性连接双球结构在轴向激励下的声辐射特性，但其研究限于100 Hz以下低频段，仅考虑了刚性振荡模态声辐射，没有计及球壳声弹性耦合作用。

针对大潜深耐压球壳结构，文献[21]建立了计及静水压力作用的厚球壳声振耦合模型，计算分析了厚壁几何特征和静水压力载荷对球壳声振耦合特性的影响。在其研究基础上，本文进一步针对大深度载人潜器的多球壳组合结构，以水介质中任意空间分布的系列弹性球壳为研究对象，利用球函数平移加法定理统一表述不同球壳的辐射声场，建立计及球壳间声场相互作用的多球壳系统声振耦合计算模型，计算分析球壳间声场相互作用对不同分布的多球壳声辐射特性和空间声场分布特征的影响。

1 理论模型推导

1.1 研究对象描述

假设在无限理想声介质中有N个球壳组成的空间分布多球壳系统，如图1 所示，定义系统总体直角坐标系为O-xyz，对应的径向、经向和周向球坐标分量分别记为r、θ和ϕ。

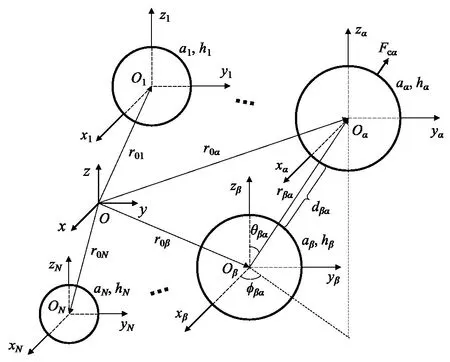
图1 空间分布多球壳系统Fig.1 Geometry of spatially-distributed spherical shells

球壳α(α=1,2,...,N)的半径和壁厚分别为aα和hα，以其球心Oα为原点建立局部直角坐标系Oα-xαyα zα，对应的局部球坐标分量记为rα、θα和ϕα，为简单起见，规定局部坐标系三个坐标轴的指向与总体坐标系对应坐标轴一致。球壳α的球心Oα在总体坐标系中的球坐标记作（r0α，θ0α，ϕ0α），在球壳β局部坐标系中的球坐标记作（rβα，θβα，ϕβα）。

1.2 单球壳振动模型

除串列球壳等特殊构型外，空间分布多球壳系统一般都是非轴对称结构体系，需要考虑非轴对称载荷作用下的单球壳振动模型。文献[21]基于一般壳体运动方程，针对轴对称激励，推导了关于球壳径向位移w的高阶振动方程：

式中，Fenm为球壳（n，m）阶径向模态激励力。

将式（2）～（3）代入式（1），利用球函数正交性，可以得到非轴对称激励下的球壳模态振动方程：

式中，Zsn为球壳模态机械阻抗，仅与模态经向阶次n有关，与周向阶次m无关。文献[21]中还考虑了剪切变形、转动惯量以及静水压力作用的影响，只需对球壳模态机械阻抗Zsn中的系数加以修正即可。

1.3 多球壳系统的相互作用载荷

引入外场声介质作用，多球壳系统第α号球壳受到的径向载荷可分为三部分，除了径向机械激励力载荷外，还有球壳α产生并作用于自身表面的声压载荷以及其它球壳产生并作用于球壳α表面的声压载荷，其中，每个球壳产生的声压又可分解为弹性辐射声和刚性散射声两部分。因此，球壳α受到的径向载荷可表示为

各子球壳的辐射和散射声压一般采用各自局部坐标系下的球函数进行模态展开，由于不同局部坐标系下的球函数通常不具备正交性，在处理球壳表面边界条件时会存在较大困难。借助球函数平移加法定理，则可以将不同系列球函数都变换到同一个坐标系下，实现多球壳声压载荷表述形式的统一。因此，将球壳β产生并作用在球壳α表面的弹性辐射声压和刚性散射声压都变换到球壳α局部坐标系下，分别得到

1.4 多球壳系统声振耦合模型

将单球壳模态振动方程式（4）右端的机械激励模态力替换为包含机械激励和声压载荷的式（12），得到考虑球壳间声场相互作用的球壳声振耦合方程：

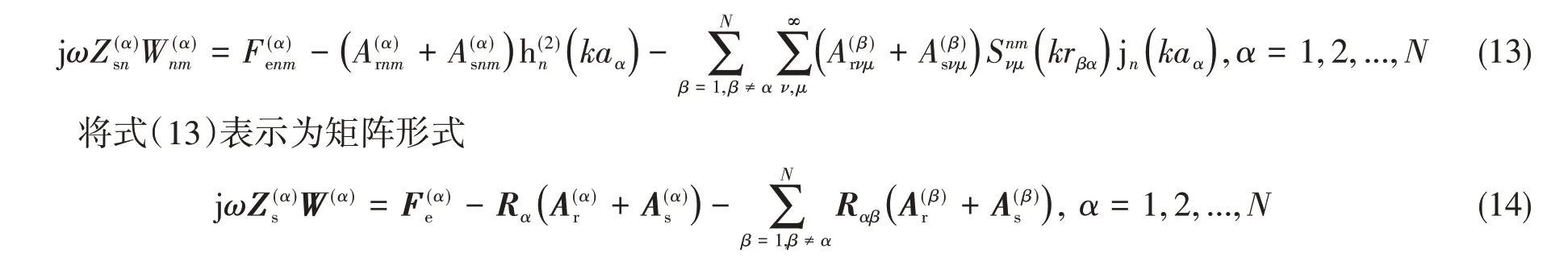
将辐射、散射声压及径向位移模态展开式代入式（15）～（16），借助球函数平移加法定理，可以得到模态声压和模态位移应满足的关系式，写成矩阵形式有

求解式（22）得到多球壳系统的模态位移，再代入式（20）和式（21）求得模态声压，进而可以计算多球壳系统的耦合振动响应和辐射声场。

如果将矩阵R和H中表征球壳间声场相互作用的子矩阵元素Rαβ和Hαβ都置为0，则可以得到解耦的多球壳系统振动方程，也就是各球壳自身的声振耦合方程

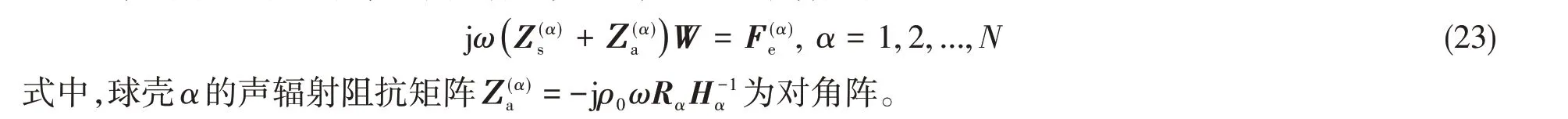
1.5 多球壳系统辐射声场计算

外场声介质中任一场点( )r,θ,ϕ的辐射声压可通过叠加每个球壳在该场点的弹性辐射声和刚性散射声得到

2 计算模型验证

选取相同尺度的2个球壳组成双球壳系统模型，基本参数如下：球壳半径为1 m、壁厚为20 mm，球心距为2.1 m，材料选用钛合金，密度为4500 kg/m3，杨氏模量为110 GPa，泊松比为0.34，结构阻尼因子取0.005，水介质密度和声速分别取1000 kg/m3和1500 m/s。

双球壳布置如图2 所示，两个球心均位于y轴，采用上章建立的模型计算单位机械点力激励下双球壳系统的耦合振动与声辐射，并与COMSOL 数值计算结果进行比对，激励力方向取θe1=90°。由于双球壳系统及其激励载荷相对极轴（z轴）均为非轴对称布置形式，因此需要计及各阶周向模态的贡献，计算中取N=M=15。

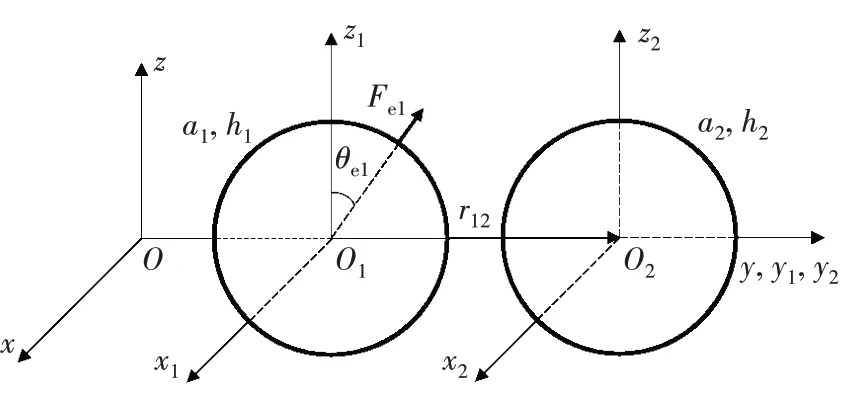
图2 双球壳系统Fig.2 Geometry of double spherical shells

由图3给出的双球壳系统辐射声功率曲线可以看到，本文解与COMSOL 解基本重合，在高频段略有偏差，此外，两种方法计算的双球壳辐射声压空间分布也吻合较好，参见图4，证明了本文建模方法的正确性。

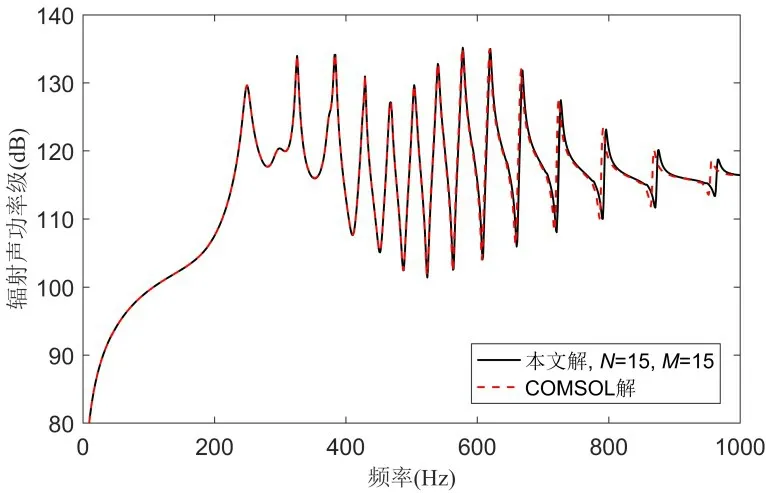
图3 双球壳系统的辐射声功率Fig.3 Acoustic radiation power by double spherical shells

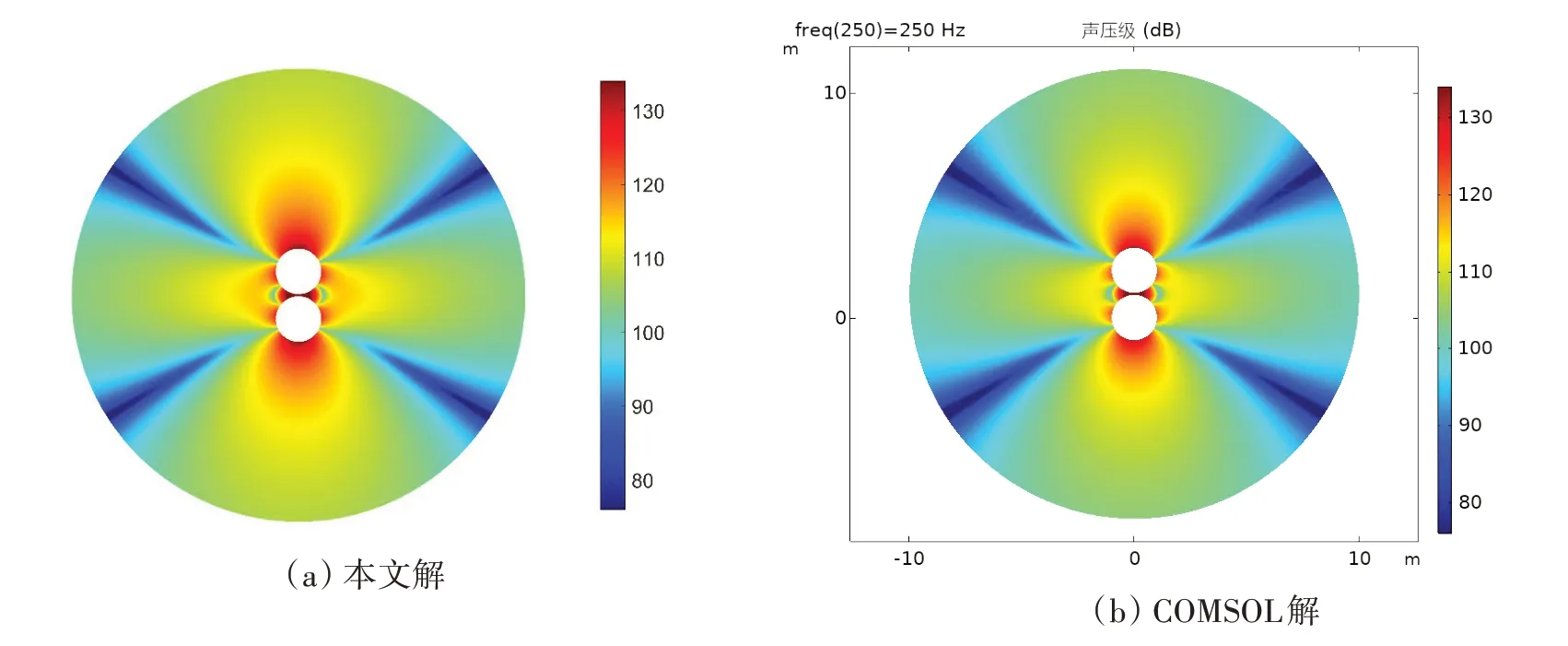
图4 双球壳系统的耦合辐射声场（f=250 Hz）Fig.4 Acoustic pressure field of double spherical shells

3 多球壳系统的声场耦合特性

3.1 互辐射阻抗分析

以如图5所示的轴对称布置双球壳为例计算分析多球壳系统辐射阻抗特性，不失一般性，考察m=μ=0 的情况，系统声辐射阻抗矩阵可以简化为

图5 轴对称布置双球壳系统Fig.5 Geometry of axial symmetric double spherical shells

将矩阵元素记为Z，其中，Z定义为球壳i的模态自辐射阻抗，表示球壳i的n阶模态对自身模态振动的影响；Z定义为球壳i的模态互辐射阻抗，表示球壳i的ν阶模态对n阶模态振动的影响；Z定义为球壳i和j之间的球壳间模态互辐射阻抗，表示球壳j的ν阶模态对球壳i的n阶模态振动的影响。

以1号球壳的模态自辐射阻抗幅值为基准，图6显示了球壳模态互辐射阻抗和球壳间模态互辐射阻抗的对比。由图可见，由于球壳间模态声场的耦合作用，使得原本互不耦合的球壳声辐射模态之间也产生了一定程度的耦合，相应的互阻抗幅值最大超过自阻抗幅值的30%，但是，球壳间模态互阻抗幅值则要明显大于球壳自身的模态互阻抗幅值，表明了两球壳声场间的强耦合关系。

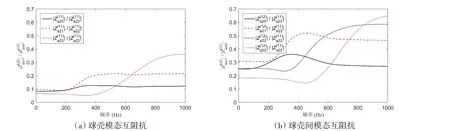
图6 模态声辐射互阻抗Fig.6 Modal mutual acoustic impedance

图7对比了单阶模态振动对壳体振动的贡献，可以看到，单球壳模型的单阶模态振动只对壳体振动的单个峰值有贡献，而由于不同球壳模态间的声场耦合作用，双球壳模型的单阶模态振动对壳体振动的多个峰值都有贡献，说明双球壳模型的壳体振动响应峰值是多阶次模态振动叠加的结果。

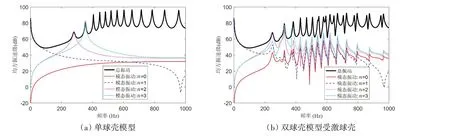
图7 单阶模态振动对壳体振动的贡献Fig.7 Contribution of modal vibration to the shell vibration

3.2 多球壳耦合声振特性分析

图8和图9分别显示了单球壳和双球壳模型的壳体振动响应与辐射声功率的对比。可以看到，与单球壳模型相比，除个别低阶峰值外，双球壳模型的壳体振动幅值明显下降，且非受激球壳和受激球壳的峰值振动响应在同一量级。此外，由于具有相同的几何参数和频率特征，两球壳同阶模态之间产生了相互调谐的耦合效应，类似于动力吸振器对结构共振峰值的调谐作用，使得双球壳共振峰值分离为两个峰值并分散至单球壳峰值两侧，形成峰值分叉现象。在单球壳声辐射峰值集中的200～500 Hz频段，双球壳辐射声功率峰值量级与单球壳相差不大，但峰值频率向低频偏移，而在500 Hz以上频段，双球壳比单球壳多出很多辐射峰值，这些峰值对应于壳体耦合共振的峰值位置，表征了声场耦合作用对双球壳声辐射的影响。因此，尽管从单个壳体来说，双球壳模型的振动响应弱于单球壳模型，但是双球壳的辐射声功率却要高于单球壳辐射声功率，说明球壳间声场耦合作用提高了双球壳系统的辐射效率。

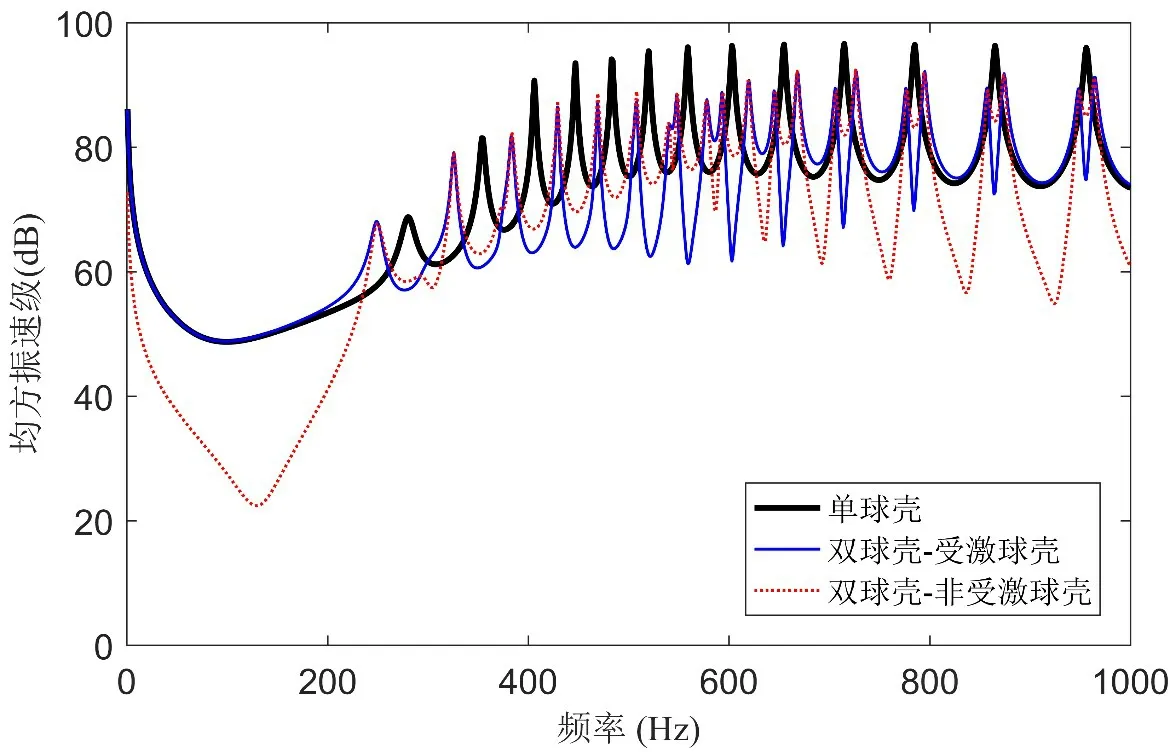
图8 单球壳与双球壳壳体振动响应比较Fig.8 Shell vibrations of single spherical shell and double spherical shells

图9 单球壳与双球壳辐射声功率比较Fig.9 Radiated acoustic power by single spherical shell and double spherical shells

由文献[21]计算结果可知，只有当球壳某一阶模态共振峰值点所对应的模态声辐射阻较高时，才能在辐射声功率曲线上有对应的局部峰值。对于单球壳来说，只有前几个低阶模态的共振频率与模态声辐射阻较高的频段吻合，因此只在200～500 Hz 频率范围内激发出了声辐射峰值。对于双球壳来说，由于声场耦合作用，球壳的低阶模态振动耦合了其他高阶模态的共振峰值特征（见图7），并且这些高阶共振峰值频率与低阶模态声辐射阻较高的频段相吻合，从而在500 Hz 以上频段也激发出了声辐射峰值。

4 多球壳系统声场耦合的影响因素

针对空间分布系列球壳的不同组合及参数，研究对比单球壳和多球壳系统的声场耦合与辐射特性，计算分析球壳间距、激励方向、尺度比和布置方式等因素的影响，球壳半径取2600 mm，壁厚取95 mm，其他计算参数同第2章。

4.1 球壳间距的影响

如图5所示，建立由相同尺度球壳组成的轴对称布置双球壳模型，定义球壳分布系数d12为两球壳球心距与半径之和的比值，即d12=r12/(a1+a2)，在1 号球壳北极点施加径向单位机械点力，对比球壳分布间距对系统声场耦合特性的影响。

由图10 可以看到，当d12小于1.1 时，由于两球壳间的强声场耦合作用，虽然双球壳中的受激球壳振动小于单球壳振动，但非受激球壳振动并没有显著小于受激球壳，并且双球壳系统的壳体耦合振动在单球壳各阶峰值频率处分离为两个峰值。随着间距加大，受激球壳振动逐渐增加，非受激球壳振动则有所减小，且振动峰值分叉现象出现的频率范围逐步往低频一侧收窄，当d12达到2.0 时，受激球壳振动已基本接近于单球壳模型，而非受激球壳则仅在低频段剩余少量振动峰值，且幅值很小。

图10 球壳间距对双球壳系统壳体耦合振动的影响Fig.10 Influence of spacing on shell vibrations of double spherical shells

图11 给出了双球壳n=4 阶模态对应的低频方向峰值的近场声压分布。由图可见，不仅受激球壳产生辐射声场，非受激球壳也产生辐射声场，随着球壳间距的增大，双球壳相对单球壳的声辐射峰值频率迁移量逐渐减小，由d12=1.01时的15 Hz减小到d12=2.0时的0 Hz。受激球壳周围的近场声压分布也逐步趋近于单球壳，当d12达到2.0时，除了在非受激球壳一侧的60°立体角范围，其余方向声压分布形态与单球壳模型基本一致，说明此时球壳间声场耦合的影响已基本可以忽略。

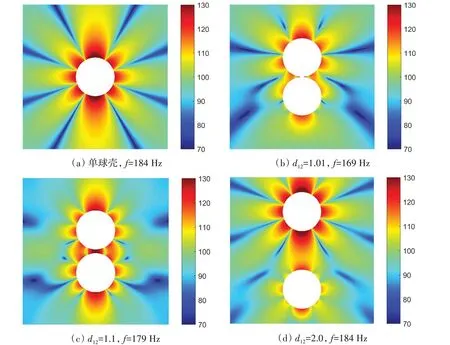
图11 球壳间距对双球壳系统耦合辐射声场的影响Fig.11 Influence of spacing on acoustic pressure fields of two spherical shells

4.2 激励方向的影响

针对4.1 节双球壳模型，计算对比激励力作用方向对双球壳系统声场耦合特性的影响，计算中取d12=1.05。图12 和图13 给出了机械点力沿不同极角方向激励时双球壳系统辐射声功率。由图可见，轴向激励时，球壳间声场耦合效应较强，由于两球壳同阶模态间的相互调谐作用，使得双球壳辐射声功率峰值不再对应单球壳峰值，且300 Hz 以上中频段还出现了若干新峰值，从幅值上看，100～200 Hz频率范围内峰值幅值与单球壳相当或略有减小，200 Hz以上的峰值则大幅提升，参见图12。随着激励力偏离轴向，双球壳的辐射声功率峰值逐渐向单球壳峰值靠拢，当激励力为正横方向90°时，双球壳声辐射峰值已趋近于单球壳，球壳间声场耦合的影响减至最小，但主峰值的最大幅值与单球壳相比仍存在3 dB左右的差别，且主峰值两侧还分布着由不同经向阶次模态相互耦合引起的小峰值，参见图13。

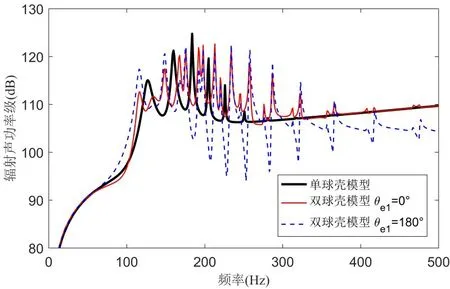
图12 轴向激励下双球壳系统辐射声功率Fig.12 Acoustic radiation power by double spherical shells under axial excitation

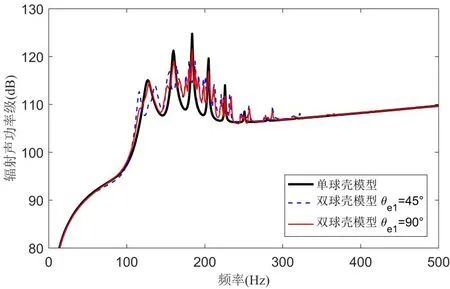
图13 非轴向激励下双球壳系统辐射声功率Fig.13 Acoustic radiation power by double spherical shells under non-axial excitation

图14给出了n=4阶模态对应声辐射峰值的近场声压分布，沿轴向激励时，非受激球壳与受激球壳的近场声压形态对称分布，且每个球壳沿周向的波瓣数量与图11（a）中的单球壳模型一致，表明振动能量在两个球壳间得到了充分交换，反映了声场耦合效应的显著影响；沿横向激励时，双球壳系统的声辐射主瓣分布在激励力所在的正横方向，说明相邻球壳的声场相互作用对系统声辐射的指向性产生了一定影响。

图14 不同方向激励时声辐射峰值（n=4阶）的耦合声场分布Fig.14 Acoustic pressure fields of double spherical shells under excitation from different directions

4.3 球壳尺度比的影响

保持球壳厚径比不变，改变双球壳中2 号球壳半径，将两球壳半径之比取为a21=0.5，计算分析球壳尺度比对系统声场耦合特性的影响，算例中单位机械点力施加在1号球壳正横方向，即θe1=90°，并取球壳分布系数d12=1.05。

图15 显示了不同尺度比双球壳系统的辐射声功率对比。由4.2 节可知，正横方向激励时球壳间声场耦合效应相对较小，因此，相同尺度球壳组成的双球壳系统的声辐射峰值仍主要集中在单球壳峰值所在的100～300 Hz频段，而当球壳尺度比变为0.5后，在250～500 Hz频段也出现了数个幅值较高的峰值，这表明当球壳尺度比变小时，声场耦合效应影响的频段向高频有所拓展。表1列出了两种尺度球壳在水中单独受激时的声辐射峰值频率，可以看到，尺度较小的非受激球壳在单独受激时的声辐射峰值正好位于250～500 Hz，也就是说，该频段集中了具有强辐射特征的非受激球壳低阶模态。因此，尽管受激球壳在该频段内的模态声辐射能力较弱，但却能够通过近场的声场耦合激发起非受激球壳的低阶强辐射模态并向外场辐射声能量，形成相应的耦合声辐射峰值。此外，由于球壳尺度越大，模态固有频率越低，因而当球壳尺度比增大时，双球壳系统声辐射的强耦合频段将向低频方向拓展。

表1 球壳单独受激时的模态峰值频率Tab.1 Modal frequencies of excited single spherical shell

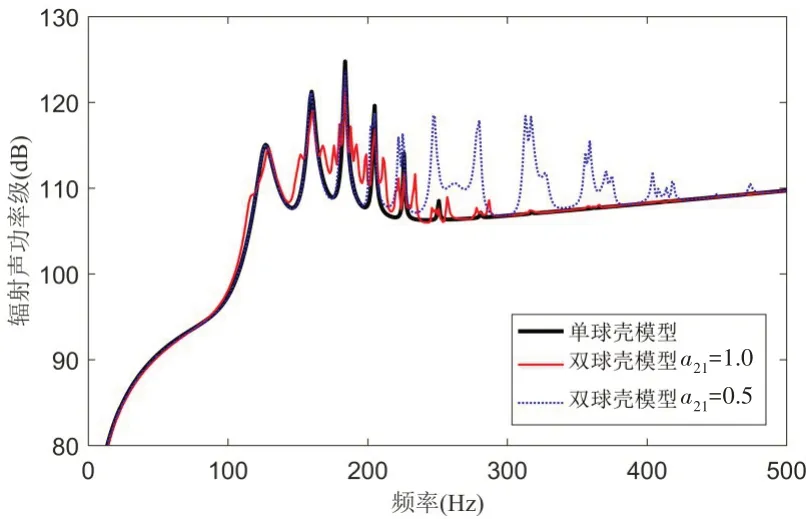
图15 不同尺度比双球壳系统的耦合声辐射Fig.15 Acoustic radiations of double spherical shells with different scale ratios

图16 给出了不同频段声辐射峰值对应的近场声压分布，可以看到，184 Hz 频率上主要是由受激球壳自身受激形成的辐射声场，247 Hz频率上主要是由受激球壳n=7阶模态与非受激球壳ν=2阶模态相互耦合形成的辐射声场，而280 Hz频率上则是由受激球壳n=8阶模态与非受激球壳的ν=2和ν=3两个阶次模态同时耦合形成的辐射声场。

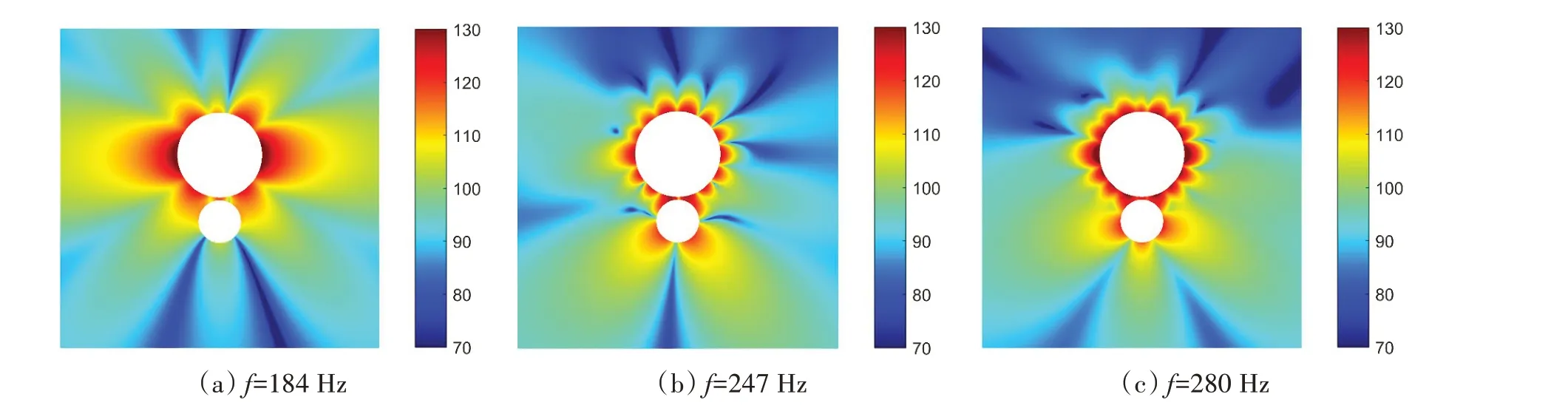
图16 不同尺度球壳间模态耦合形成的辐射声压场Fig.16 Acoustic pressure fields of double spherical shells of different sizes

4.4 球壳布置方式的影响

在图5双球壳模型基础上，沿轴线方向增加相同尺度的球壳，组成串列布置的三球壳和四球壳系统，进一步计算分析串列多球壳系统的声场耦合特性。假定单位机械点力施加在1号球壳90°正横方向，相邻球壳的分布系数统一取1.05。图17 给出了峰值频率处的空间声场分布，与双球壳系统类似，串列三球壳系统和串列四球壳系统也能够在各球壳之间形成强声场耦合效应，尽管3号（4号）球壳离受激的1 号球壳较远，但也包含在系统声场耦合之中，说明声场耦合效应具有一定的传递作用。此外，由于低阶（n=3 和n=4）峰值频率对应的声波波长较长，受激球壳对较远处非受激球壳的辐射声场也有显著影响，使得非受激球壳外场形成了大范围亮区，随着模态阶次加大，非受激球壳的辐射亮区逐渐收缩至各球壳紧邻区域。

以三球壳系统为例，研究球壳分布角度对耦合辐射声场的影响，建立如图18 所示的分布式三球壳系统模型，假定各球壳尺度相同，其中，1 号和3 号球壳关于2 号球壳球心所在水平面对称布置，1、2号球壳球心连线O1O2与2、3号球壳球心连线O2O3的夹角定义为α13，激励力施加在2号球壳90°正横方向，2号与1号、2号与3号球壳间的分布系数均取1.05。

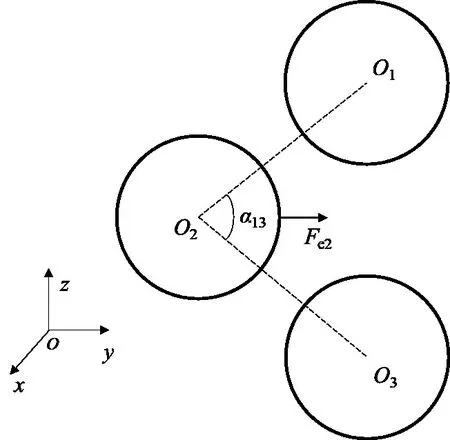
图18 分布式三球壳系统Fig.18 Geometry of distributed triple spherical shells

由图19可以看到，随着球心夹角α13的减小，三个球壳逐渐靠近，相互之间的声场耦合效应相应增强，三球壳系统声辐射峰值相对单球壳峰值的频率偏移量逐步加大，并出现局部附加声辐射峰值。从辐射声压空间分布形态来看，在α13=180°时，辐射亮区主要分布在与三球壳轴线平行的横向区域，随着分布角度的改变，辐射亮区逐渐集中到三球心连线构成的三角区域，辐射声场空间分布更趋复杂，参见图20。

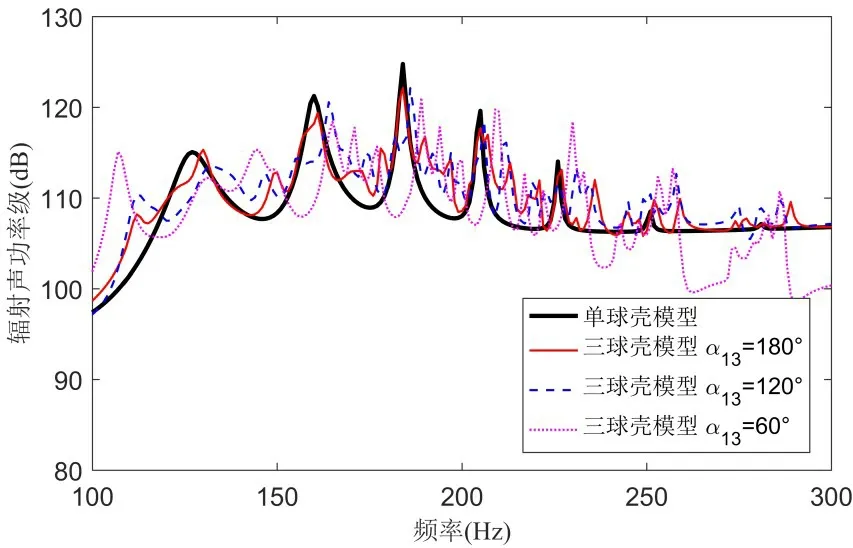
图19 分布式三球壳系统辐射声功率比较Fig.19 Acoustic radiation powers of distributed triple spherical shells

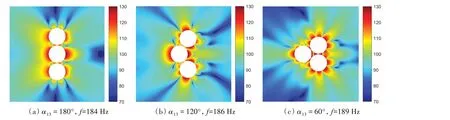
图20 不同布置形式三球壳系统的空间声场分布Fig.20 Acoustic pressure fields of distributed triple spherical shells

5 结 论

本文针对任意空间分布系列球壳组成的多球壳系统，基于非对称载荷作用下的球壳动力学模型，借助球函数平移加法定理统一表述不同球壳的辐射声场，建立了计及球壳间声场相互作用的多球壳系统声振耦合计算模型。在计算分析多球壳系统互辐射阻抗和耦合声振特性基础上，研究了球壳间距、激励方向、球壳尺度比及布置方式等因素对多球壳系统辐射声功率的影响规律，结果表明上述因素对多球壳系统声振特性都有显著影响，得到的下列一般性结论可以为水下多球壳组合结构声学设计提供参考。

（1）由于多球壳间的声场相互作用，不仅使原本解耦的单球壳不同经向阶次模态之间形成一定程度的耦合，而且球壳间模态互阻抗也明显大于球壳自身的模态互阻抗，使得单阶模态振动对球壳振动的贡献不再限于单个振动峰值，进而影响了多球壳系统的声辐射效率及频谱特征。

（2）在声场耦合作用下，同一尺度双球壳系统的受激球壳和非受激球壳都产生声辐射，轴向激励时，两球壳间存在强声场耦合效应；随着球壳间距增大，非受激球壳耦合振动逐渐减小，受激球壳典型声辐射峰值的声压空间分布形态逐步趋近于单球壳；当激励力偏离轴向时，声场耦合效应也逐渐减弱，正横方向时，耦合最小。

（3）不同尺度球壳组成的双球壳系统扩展了声场有效耦合的频率范围，相应辐射声场具有两个球壳各自的模态特征，并在非受激球壳低阶强辐射模态对应的特征频率附近产生新的辐射峰值。

（4）多球壳串列布置时，声场耦合效应具有传递作用，频率较低时，非受激球壳附近形成大范围辐射亮区；多球壳按不同角度分散布置时，随着分布角度减小，声场耦合效应增强，不仅出现附加声辐射峰值，而且辐射声场空间分布更趋复杂。