线性二次型球式滚动机器人运动稳定性研究与测试分析
袁 飞
(常州轻工职业技术学院 校企合作处,江苏 常州 213000)
近年来,由于新技术的发展和整个应用市场的拉动,机器人在各个行业的应用越来越广泛,如医疗、包装、制造及航天等.单球滚动式机器人作为一种运动灵活、通过性好的机器人,在各行业均具有巨大发展潜力[1].
单球滚动式机器人的研究基础起源于独轮自平衡移动机器人.国内对单球滚动式机器人的研究起步较晚,虽取得了很大进展,但大部分目前仍处于理论研究阶段,未推广运用于实践中.国外对单球滚动球机器人的研究起步较早,在2005年,卡内基·梅隆大学研制出了一种新型滚动球式机器人“Ballbot”[2-7],但其动力学建模复杂且动态稳定性差.2010年,苏黎世瑞士联邦理工学院机器合作伙伴共同研制了“Rezero”机器人[8-9],“Rezero”机器人能够在球体上实现动平衡,且具有非常强的运动性,但是“Rezero”机器人与“Ballbot”机器人类似,存在动力学建模复杂且动态稳定性不足的问题.因此,为了提高单球滚动式机器人的运动灵活性及动态稳定性,本文提出利用LQR控制器对机器人的运动倾角控制算法进行设计与研究.
1 单球滚动式机器人结构设计
单球滚动式机器人的结构如图1所示,主要包括机架、驱动机构、制动抱紧机构、球体4部分组成.机架上安装有各类型的传感器、三维惯性测量单元、锂电池、控制器、伺服驱动器等;驱动机构采用直流无刷伺服电机,3个全向轮对称安装在球体上,全向轮轴线与垂直方向成30°,全向轮中心、球体中心以及它们的接触点共线;3个制动抱紧机构成120°角安装在球体四周,防止球体脱离机器人主架体的控制.
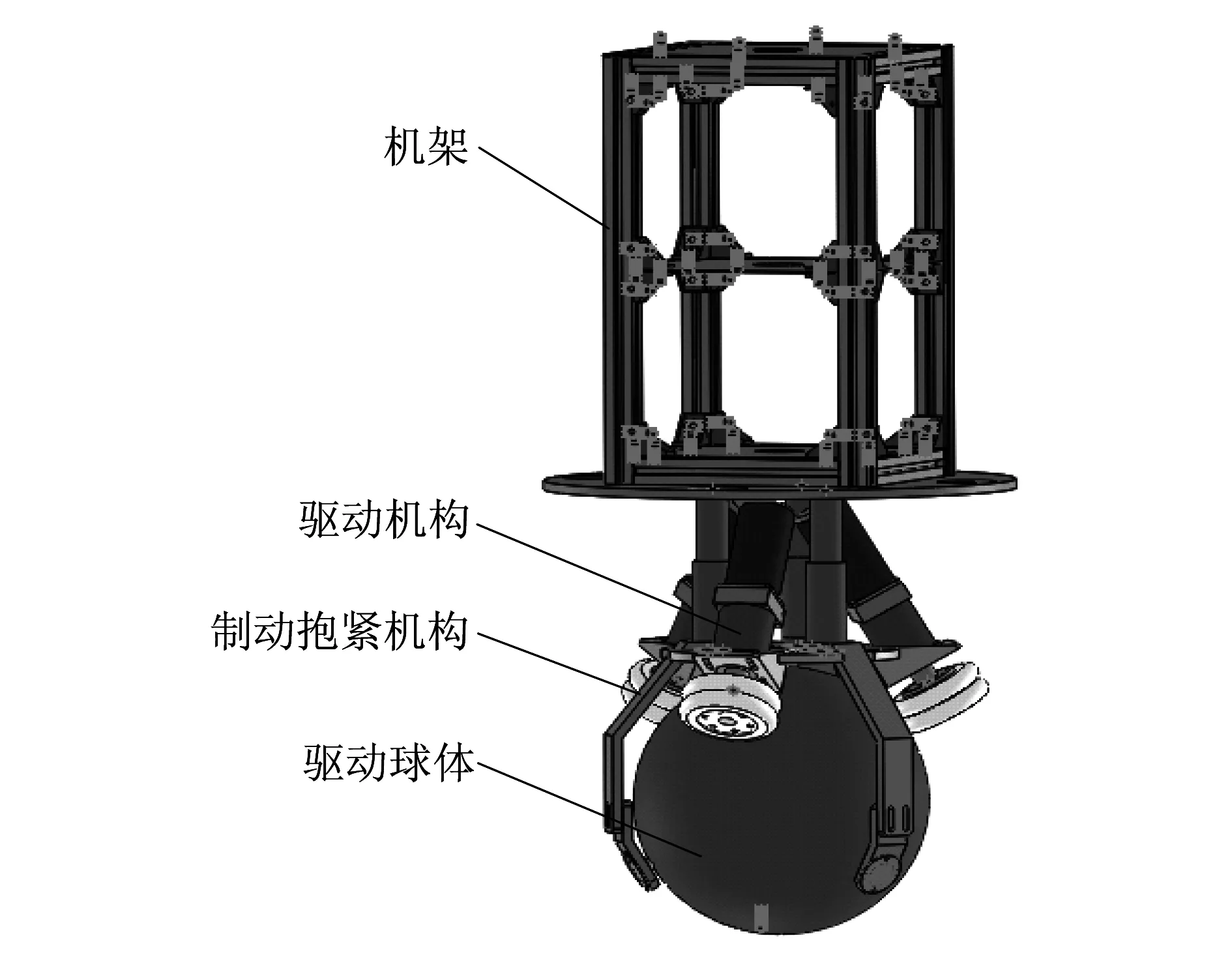
图1 滚动球式机器人本体结构Fig.1 Body structure of the rolling ball robot
由于驱动机构、制动抱紧机构、锂电池、控制器等都是固接在机架上,为了简化模型的计算,在建立模型前把固接在机架上的物体和机架当作一个整体称为主架体,故整个滚动球式机器人就可以看成是由主架体和球体两部分组成.
2 倾角控制算法设计与仿真
2.1 单球机器人动力学模型建立
单球滚动式机器人模型可以等效为x向和y向两个单级倒立摆模型.由于两个方向的等效单级倒立摆模型的理论基础、建模方法以及相应的控制策略均是相同的.因此,只需对单球滚动式机器人两个等效单级倒立摆模型中的一个进行动力学建模分析即可.以单球滚动式机器人x向的等效单级倒立摆模型为例,运用Euler-Lagrange方程对其进行动力学建模.
假设机器人底部的运动球体与地面和全向轮之间均做无滑动的纯滚运动,则运用Euler-Lagrange方程,对x向的等效单级倒立摆模型进行动力学建模[10-13]:
(1)
式中:

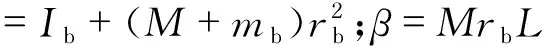
脂肪酸酯也可发生此类反应生成a-单磺酸化脂肪酸酯[18],此反应常被用来制备类似结构的表面活性剂,产品易降解且对环境近无危害。
综合以上各式,得出等效x向单级倒立摆模型的动力学方程如下:
(2)
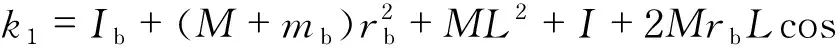
据式(2)再结合单球滚动式机器人的相关设计参数,便可求出单球滚动式机器人x向的等效单级倒立摆模型的动力学模型.
2.2 基于LQR机器人运动控制器设计
LQR控制器又称为线性二次型调节器,在现代控制理论中,LQR是发展较早且相对比较成熟的一种状态线性反馈控制算法,易于构建闭环最优控制.LQR运动控制器的控制对象主要是以状态空间形式所表示的线性系统,其目标函数为控制输入和对象状态的二次型函数.LQR最优控制原理是利用所设计的状态反馈控制器K,使二次型目标函数J取得最小值,其中K值是由权矩阵Q和R决定的.因此,权矩阵Q和R的选择则显得尤为重要[14-15].
假定n阶线性系统的状态空间(r个输入变量、l个输出变量)的表达形式如下:
(3)
式中:x为n阶状态向量;y为l维输出向量;u为r维输入向量;A为系统矩阵;B为控制矩阵;C为输出矩阵;D为传递矩阵.
机器人的LQR运动控制器的系统性能指标:
二次型目标函数
(4)
控制器的控制参数
式中:Q与R为加权矩阵;K为最优控制器的控制参数;P为Riccati方程的正定对称解.
根据上文所述的单球滚动式机器人等效x向单级倒立摆系统的动力学模型及其相应状态空间表达形式,利用Matlab/Simulink软件设计了单球滚动式机器人的LQR运动状态反馈控制器,如图2所示.利用LQR控制器对单球滚动式机器人等效x向和y向单级倒立摆系统的运动状态变量进行实时控制,实现x向、y向等效单级倒立摆运动倾角与倾角角速度的有效控制.
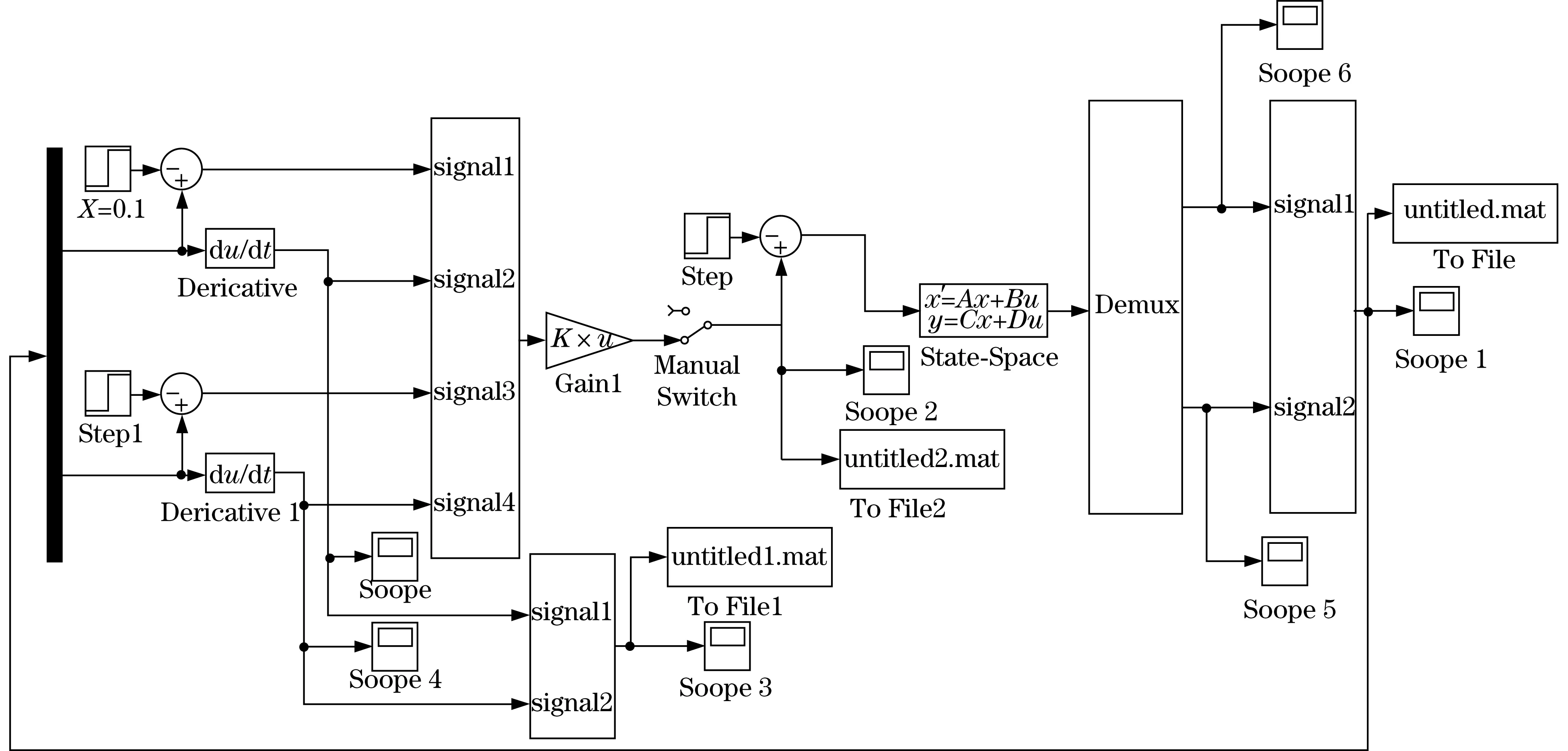
图2 LQR控制器结构图Fig.2 LQR controller structure diagram
为了获得LQR运动控制器的最优控制效果,利用Matlab/Simulink对其进行了大量的调试及仿真分析,最终确定了LQR运动控制器的加权矩阵Q和R值,即
(8)
利用Matlab调用相应lqr函数对LQR控制器的控制参数K进行求解,求解过程及求解结果如下:
K=k1k2k3k4=lqr(A,B,Q,R)
(9)
K=[-870.43 -289.97 -140.41 -240.88]
(10)
2.3 LQR控制器仿真分析
结合上文所求的加权矩阵Q,R以及控制参数矩阵K,利用Matlab/Simulink对单球滚动式机器人控制系统的LQR控制器进行仿真分析.单球滚动式机器人等效x向单级倒立摆系统动力学模型的主要状态变量的初始值可假定为
(11)
式中:θ为球体沿x,y方向的倾角;ε为x,y方向的角速度.
通过上述状态变量初始值,单球滚动式机器人的等效单级倒立摆系统x向和y向的角速度、角加速度等状态变量在LQR控制器的控制下,其运动状态变化情况如图3所示.
由图3(a)和图3(c)可以看出,单球滚动式机器人的运动倾角θx与θy,在相应设定的扰动下,通过LQR运动控制器的调节,能够使整个机器人运动系统在2 s左右快速恢复到平衡状态.图3(b)和图3(d)分别是单球滚动式机器人等效x向单级倒立摆和等效y向单级倒立摆的运动倾角角速度在相应干扰下的运动情况,由图可知,机器人的倾角角速度在2 s左右能够重新恢复到平衡状态.由图3(e)可知,整个控制系统的u曲线的超调量大约为60%,稳定时间在0.8~1.0 s之间,该指标系数符合系统状态控制的规定,达到了运动系统状态控制的要求.
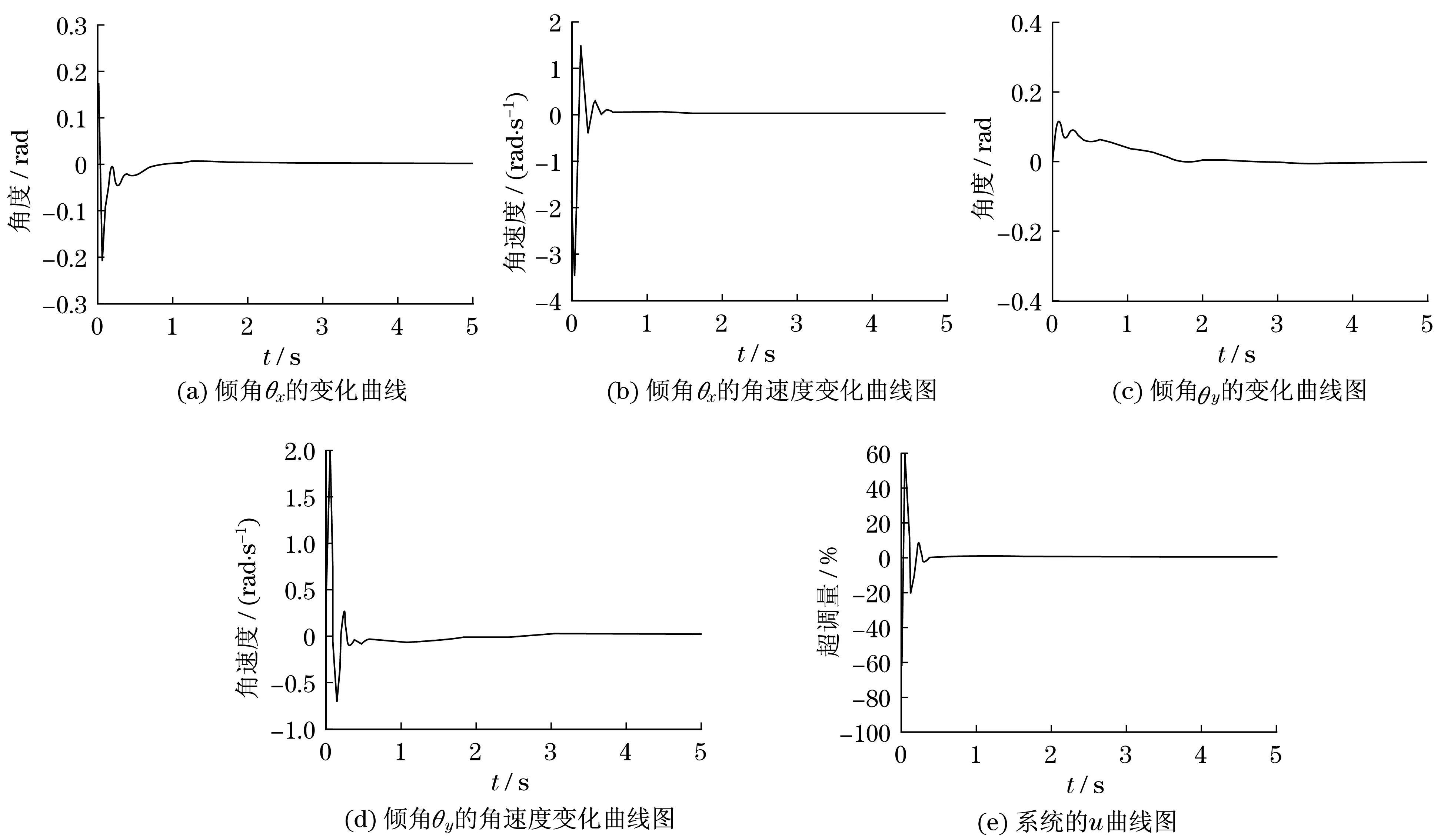
图3 状态变量仿真分析曲线图Fig.3 Simulation analysis curve of state variables
根据上述仿真结果分析可知,以单球滚动式机器人的动力学模型为基础,设计相应的LQR运动状态控制器能够很好地实现等效x向、等效y向单级倒立摆的倾角与倾角角速度等状态变量的运动控制,从而实现整个单球滚动式机器人的运动控制.
3 测试分析
单球滚动式机器人的试验样机如图4所示,为了验证上文所设计的LQR运动控制器对单球滚动式机器人的控制效果,设定了一个从(0,0)到(5,5)的实验路径,并利用DSP控制器、IMU(惯性导航模块)及示波器等实时观测机器人的运动情况.首先,将单球滚动式机器人利用外设辅助机架吊起来;然后,打开机器人的运动控制开关,并进行调试实验,当机器人运动稳定后解除辅助机架,使其沿固定轨迹运行,机器人倾角θx,θy的变化情况及运动轨迹分别如图5~图7所示.
由图5可知:单球滚动式机器人在0~2 m时,运动抖动较为明显,无法保持一个较为平衡的状态;在2 m之后,机器人在LQR运动倾角控制器的调节下,运动趋于平衡稳定,并具备了一定的自平衡调节功能.由图6和图7可知:机器人在整个运动过程中倾角θx,θy基本在5°之内且变化不大,符合前文所述的机器人运动倾角的变化规律.根据上述实验结果可知,利用LQR所设计的运动状态控制器以及相对应的控制算法对单球滚动式机器人的运动稳定性控制是有效、合理以及正确的.

图4 试验样机图Fig.4 Test machine diagram
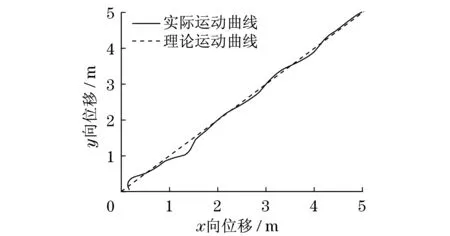
图5 试验曲线图Fig.5 Test curve

图6 倾角沿x方向的变化情况Fig.6 Variation of pitch angle along x direction
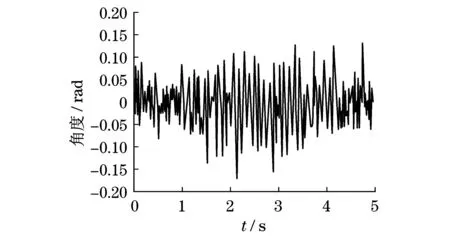
图7 倾角y方向的变化情况Fig.7 Variation of pitch angle along y direction
4 结论
(1) 针对当前单球滚动式机器人运动不灵活、动态稳定性差等问题,提出了利用LQR对滚动式机器人的运动倾角进行控制,并利用Solidworks建立了机器人的三维模型.
(2) 将单球滚动式机器人模型可以等效为x向和y向的单级倒立摆模型,并运用Euler-Lagrange方程建立了机器人x向等效单级倒立摆的动力学模型.
(3) 利用Matlab/Simulink软件并结合所求的动力学模型,设计了单球滚动式机器人的LQR运动状态控制器,通过分针分析得到了相应状态变量的变化曲线图.
(4) 利用物理样机进行实验验证,结果表明,LQR运动控制器及其控制算法对单球滚动式机器人的运动控制是有效和合理的,为后续的系统优化提供了有力依据,具有较大实际意义.

