飞机整体驱动发电机可靠性评估及寿命预测

李景奎,段飞飞,蔺瑞管,王 松

(1.沈阳航空航天大学 民用航空学院,沈阳 110136; 2.中国南方航空股份有限公司 沈阳维修基地,沈阳 110100)

飞机整体驱动发电机(Integrated Drive Generator,IDG)作为航空电力系统的主要电源,工作在高空、低温、低压等恶劣环境下,其安全可靠是飞机正常飞行的重要保证.进行IDG可靠性评估及寿命预测研究,有利于找出IDG故障的变化规律,提高飞机的安全性和可靠性.目前进行可靠性评估及寿命预测研究主要方法是利用威布尔分布对故障数据进行可靠性建模,运用Bootstrap方法或似然比检验理论求解可靠度、平均故障间隔时间的点估计及区间估计[1-7],可以获得比较准确的评估及预测结果.但是对于工程实际中常见的故障数据服从任意分布、概率密度函数及概率分布函数难以确定的情况,上述方法运算过程复杂,计算量庞大.

利用Edgeworth级数法可以很好地解决这类问题.文献[8-9]采用随机变量的各阶矩构造概率分布函数,指出了高阶矩对计算结果有较大影响.文献[10]对比了3种不同级数逼近概率密度函数渐近展开式的方法,并分析比较了偏态系数和峰度系数在不同取值范围时的差异.Edgeworth级数方法可以把服从任意分布的故障数据概率分布函数近似展开成标准正态分布函数的方式进行研究[11-13].

本文利用Edgeworth级数方法,把服从任意分布的故障数据概率分布函数近似展开成标准正态分布函数,进而求得IDG可靠度与平均故障间隔时间的点估计,并运用Bootstrap方法进行IDG可靠度及平均故障间隔时间的点估计和区间估计计算,通过算例验证了本文方法的正确性和有效性.

1 可靠性指标Edgeworth级数评估及预测方法

设fY(Y)为服从任意分布的故障数据联合概率密度函数,应用联合正态概率密度函数的偏导数集合,可以近似地获得任意分布函数fY(Y)的表达式

(1)

式中:jT=j1+j2+…+jN;Y=[Y1,Y2,…,Yn]T为状态空间向量;函数φY(Y)为联合概率密度函数,

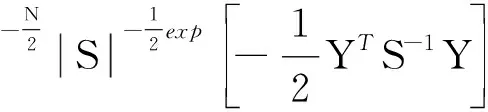
(2)

式中:S为状态空间向量的协方差矩阵.

式(1)中的rj1j2…jN为展开式的系数,展开式系数选取的不同,得到的分布函数表达式也会有所不同.

(3)

式中:ci(i=1,2,…，n)为待定系数;φ(y)为标准高斯分布N(0,1)的分布密度;φ′(y),φ″(y),φ‴(y),φ(4)(y)分别为φ(y)的1～4阶导数.

从式(3)中可以看出,待定系数ci(i=1,2,…，n)是未知的,故计算ci则需要从Hermite多项式的定义出发:

(4)

式中:[n/2]为n/2的整数部分,计算结果为

同时,Hermite多项式在权函数e-y2/2(y∈R)下是正交的,即

(5)

式(5)可以转化为

(6)

因此

(7)

通过计算,可得到待定系数ci(i=1,2,…，n)的值如下:

把待定系数ci(i=1,2,…，n)的值代入式(3),并对两边积分,根据Edgeworth级数方法,便可以把服从任意分布的故障数据的概率分布函数近似展开成标准正态分布函数,即

(8)

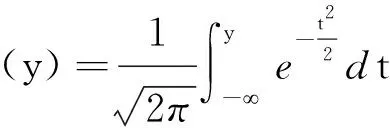
以下是式(8)中标准化了的故障数据y的前四阶矩,即均值μy、标准差σy、偏度θy、峰度ηy,

式中:yj(j=1,2，…,n)为第j个标准化故障数据.

根据式(8),把服从任意分布的故障数据概率分布函数近似展开成标准正态分布函数的表达式时,通常其概率密度函数是非对称的,则IDG整机可靠度可表示为

(9)

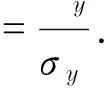
用式(9)计算IDG可靠度时,会有R>1的情况出现.当R>1时,采用下述经验修正公式修正;当没有R>1的情况出现时,Edgeworth级数可以获得足够精确的解,

(10)

Edgeworth级数可以任意精确逼近服从任意分布的故障数据概率分布函数,且通常取级数的前4项即可得到较好近似.因此,更接近于工程实际.Edgeworth级数法评估及预测IDG整机可靠性指标步骤如图1所示.

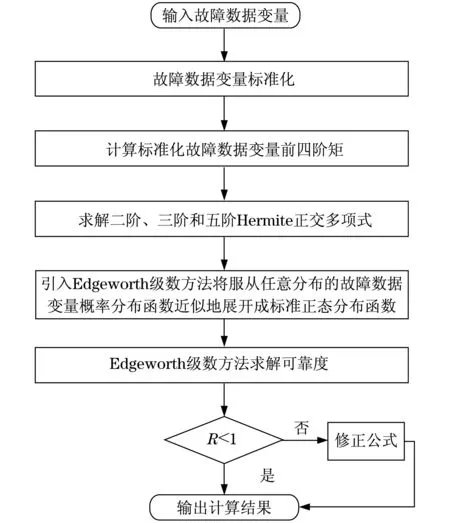
图1 飞机IDG可靠性指标Edgeworth级数法评估及

2 可靠性指标Bootstrap评估及预测方法

Bootstrap方法是通过重抽样来构造重抽样样本,用于参数的点估计和区间估计.其基本思想如下[14-15]:

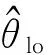
3 实例分析

基于航空维修工程中飞机IDG故障数据,对统计记录的数据进行预处理,得到的故障数据如表1所示.

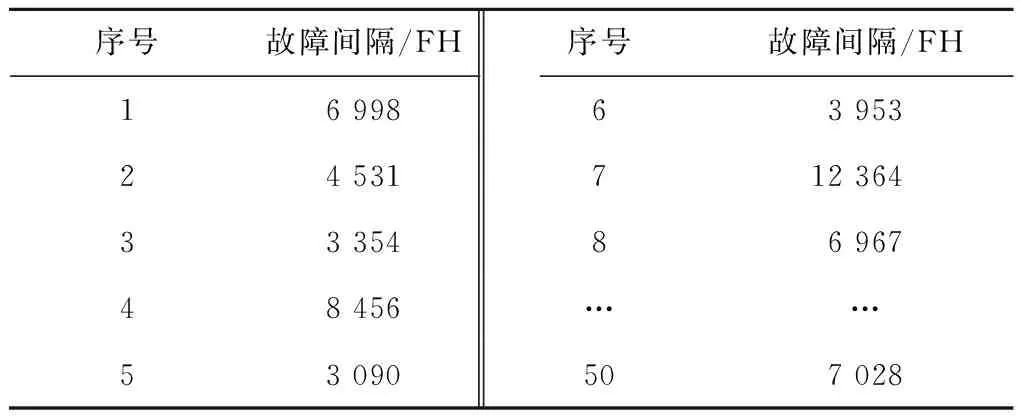
表1 飞机IDG故障间隔时间数据Tab.1 Aircraft IDG failure interval time data s

利用Edgeworth级数法进行IDG可靠性评估及寿命预测,不需要参数估计、假设检验等步骤确定故障数据所服从的分布,直接将服从任意分布的故障数据概率分布函数近似展开成标准正态分布函数即可.按照本文方法,获得标准化了的故障数据y的前四阶矩分别为μy=4.676 8×10-17,σy=1,θy=0.872 4,ηy=2.781 0.将y的前四阶矩作为Edgeworth级数展开式中的系数代入式(8),得到飞机IDG整机可靠度为R=0.442 0,TMTBF=7 246.700 0.

根据Bootstrap方法,采用威布尔分布对故障数据进行拟合,得到1 000个服从2参数Weibull分布的Bootstrap重抽样样本,本文取置信水平γ=0.99,求得模型参数为η=8 168.500 0,β=2.396 7>1,TMTBF的点估计为7 241.000 0,区间估计为[5 918.8,8 582.50],R的点估计为0.472 8,区间估计为[0.441 3,0.499 6].

两种方法求解得到的飞机IDG可靠性指标如表2所示.

Edgeworth级数法对IDG整机可靠度与平均故障间隔时间的评估及预测结果均落在Bootstrap法评估及预测结果的区间之内,且与点估计误差较小,验证了Edgeworth级数法对故障数据展开的正确性，用于可靠性评估及寿命预测的有效性.

表2 Bootstrap法与Edgeworth级数法预测结果对比Tab.2 Comparison between the prediction results of

4 结论

(1) 利用Edgeworth级数及Hermite多项式解决了可靠性评估及寿命预测研究中故障数据服从任意分布,概率密度函数及概率分布函数难以确定,使用传统方法进行可靠性评估及寿命预测研究,运算过程复杂、计算量庞大的问题.

(2) 结合前四阶矩与Edgeworth级数展开式来逼近服从任意分布的故障数据概率分布函数,算法流程简单且易于编程,使得计算工作量大大减小.数值算例结果验证了Edgeworth级数方法对故障数据展开的正确性，用于可靠性评估及寿命预测研究的有效性.

(3) 根据预测结果可以制定更加经济合理的飞机IDG维修计划,为维修大纲的制定提供了理论参考.