改进粒子群算法优化的五连杆机器人分数阶PID控制器
许艳英,包宋建
(1.重庆创科职业学院 机电工程学院,重庆 402160; 2.重庆文理学院 电子电气学院,重庆 402160)
随着自动化产业的快速发展,诞生了许多工业机器人[1].机器人因具有工作效率高、稳定性好、安全性高等许多优点,广泛应用于汽车、航空、海洋及医疗等许多领域.机器人由于质量轻、体积小、承载能力强等特点,其动力学结构也较为复杂[2].传统的PID控制方法如果不进行改进,就会使机器人关节产生较大振动,从而影响机器人执行任务的效果.因此,研究机器人机构的合理化控制方法,对于提高机器人运动的稳定性发展具有重要的意义.
为了能够设计出更好的机器人,国内外学者采用不同控制方式对机器人进行深入研究.例如:文献[3-4]研究了机器人的改进遗传算法优化PID控制器,建立机器人关节平面关系式,提高了系统输出的稳定性;文献[5-6]研究了连杆机械臂粒子群算法优化PID控制器,有效地抑制了柔性机械臂的弹性振动;文献[7-8]研究了连杆机械臂模糊PID控制器,建立了机械臂仿真模型,提高了机器人控制响应速度和系统输出的稳定性.但是,以前研究的机器人运动控制器,其系统输出不稳定,导致输出误差较大.对此,本文建立五连杆机器人三维坐标系,推导出机器人动力学方程式,引用改进粒子群算法优化PID控制器参数,借助数学软件Simulink对机器人电动机转速响应效果进行仿真,并与传统PID控制器控制效果进行比较和分析,为提高机器人控制系统的稳定性研究提供参考依据.
1 五连杆机器人

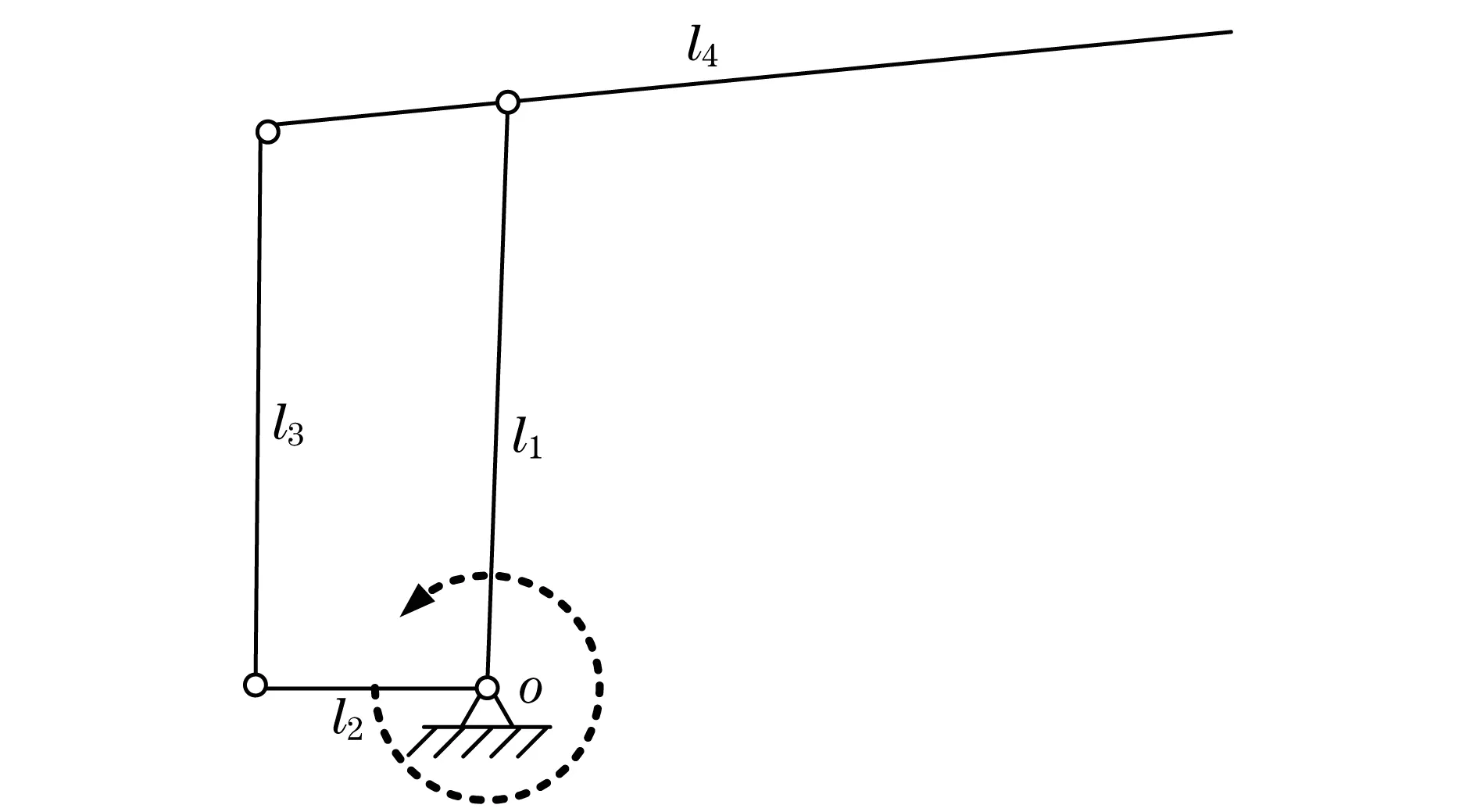
图1 五连杆机器人Fig.1 Five-link robot
机器人的动力学方程为
(1)

图2 五连杆三维模型简图Fig.2 Five-link 3D model sketch

根据Badamchizadeh方程,可得
(2)
因此,M12=M21=0,即惯性矩阵是对角且恒定的.
机器人动力学方程为
(3)
2 改进粒子群优化算法
2.1 粒子群优化算法
粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体的随机优化算法和鸟群社会行为的模拟.PSO是一个基于群体的搜索过程,其中个体用一群随机解决方案初始化,称为粒子.群体中的每个粒子都代表了优化问题潜在解决方案,如果解决方案由一组变量组成,则相应的粒子就是一个变量向量.在PSO系统中,每个粒子都在多维搜索空间中流动,根据自己和相邻粒子的经验,调整其在搜索空间中的位置.因此,粒子利用自己和邻居所遇到的最佳位置,将自己置于最佳解决方案之中.每个粒子的性能采用优化问题特征的预定义适应函数进行评估.
PSO的核心操作是粒子的更新公式,即速度和位置更新公式,PSO[9-10]全局优化模型为
式中:ω为惯性权重因子;vi(t)为粒子i在迭代t次的速度;xi(t)为迭代t次的粒子位置;C1和C2为粒子加速度系数;R和r为在[0,1]范围内的随机函数;Pbest(t)为迭代t次时第i个粒子的最佳位置;Gbest(t)为迭代t次时群体中所有粒子的最好位置.
2.2 改进PSO
一般来说,陷入局部最优和收敛速度慢是原始PSO的两个主要弱点.在本文中,采用改进方法来克服原始PSO的上述弱点.
在提供精确解决方案之前,原始PSO的收敛速度慢与速度更新公式中缺少任何自适应时变加速器密切相关.在式(4)中,系数C1和C2的确定是通过Pbest和Gbest的粒子运动的步长.因此,在原始粒子群算法中,算法步长大小对群体中的所有粒子都大致恒定.在优化复杂多模态函数时,这些常量不能满足算法收敛要求.有必要建立一种更精确的加速算法运动机制.一种机制是使用时间变化的步长,引入了更敏感和更快的运动.为此,可以采用迭代中成本函数的值,在每次迭代中,成本函数的值是对原始粒子速度的改进.当找到新的个体最佳位置时,它意味着在搜索空间中的一个更好的路径(解决方案)是由一个粒子来探索的.在新找到的方向上的加速运动,可以很快地使粒子处于良好的路径中,引入新的全局最佳位置意味着群体在整个搜索空间中发现更好的路径(解决方案).在不同迭代中,成本函数值之间的差异可以选择为PSO的加速器.本文提出了在式(4)中引入两种时变倍增器的方法.在这种情况下,时变加速器可以提供更灵敏和自适应的运动.本文将原始速度更新公式修改如下:
(6)
式中:f[Pbest(t)]为第i个粒子在迭代t次找到的最佳适应度函数;f[Gbest(t)]为群体迭代t次的最佳目标函数.
3 改进分数阶PID控制
3.1 分数阶PID控制
分数阶PID控制器用于改善动态响应并减少稳态误差,分数阶PID控制器的传递函数[11]描述如下:
(7)
式中:KP,KI和KD分别为比例、积分和微分系数;λ和μ为分数幂.
为了设计最佳的PID控制器,应该根据一些期望的规格来定义代表系统要求的、合适的目标函数.在控制设计中主要考虑3种性能指标,分别为综合绝对误差(IAE)、平方误差积分(ISE)和时间加权平方误差积分(ITSE).采用不同的性能指标为最佳的PID控制器提供了不同的解决方案.IAE,ISE和ITSE性能标准公式定义如下:
在本文中,另一个时域性能准则定义为
(11)
式中:K为参数向量,K=[KP,KI,KD,λ,μ];e为误差;Mp为超调量;Ess为稳态误差;Tr为上升时间;Ts为调整时间;α为加权因子,α的最佳选择取决于设计者的要求和受控设备的特性,可以将α设置为小于0,以减小稳态误差.
3.2 改进分数阶PID控制
为了设计最佳的PID控制器,关于最小化性能指标的矢量K=[KP,KI,KD,λ,μ]的确定是主要问题.采用改进PSO的PID控制器,执行五杆机构电动机响应速度的收敛速度和稳态误差.首先,指定控制器参数的下限和上限.然后,一组初始粒子在指定范围内随机初始化.每个粒子表示解决方案(即控制器参数K),并且使用系统的阶跃响应评估每个粒子的相应性能指标.之后,所提出的改进PSO的主要过程开始如下:① 式(6)被确定;② 每个粒子的新位置使用式(5);③ 创建替代粒子;④ 重复上述过程直到满足停止标准.在这个阶段,相应于Gbest(t)的粒子被指定为最优向量K.基于改进PSO的PID控制器的设计过程如图3所示.设置初始种群大小为100,最大迭代次数为500,α=0,KP∈[0,30],KI∈[0,5],KD∈[0,5],λ∈[0,1],μ∈[0,1],γ=10,C1=C2=2,优化结果如表1所示.

图3 改进PSO寻优过程Fig.3 The optimization process of particle swarm

参数变量PSO改进PSOKP26.75 28.19KI3.923.14KD4.254.05λ0.780.92μ0.740.12
4 仿真与分析
本文采用改进PSO分数阶PID控制器,将优化结果输入到Simulink软件中进行仿真验证,机器人连杆仿真参数如表2所示.

表2 五连杆机器人仿真参数Tab.2 Simulation parameters of five-link robot
首先,随机初始化改进粒子群算法,将每个解K=[KP,KI,KD,λ,μ]发送到Simulink块,并且计算时域中的4个性能标准的值,即Mp,Ess,Tr和Ts.其次,根据所获得的性能标准针对每个解决方案评估目标函数式(11).最后,提出改进PSO的主要过程,并计算新的解.在任何迭代结束时,程序检查停止标准.当满足一个终止条件时,程序停止,最新的全局最优解返回为K的最佳解.所提出的程序Simulink如图4所示,仿真结果如图5所示.
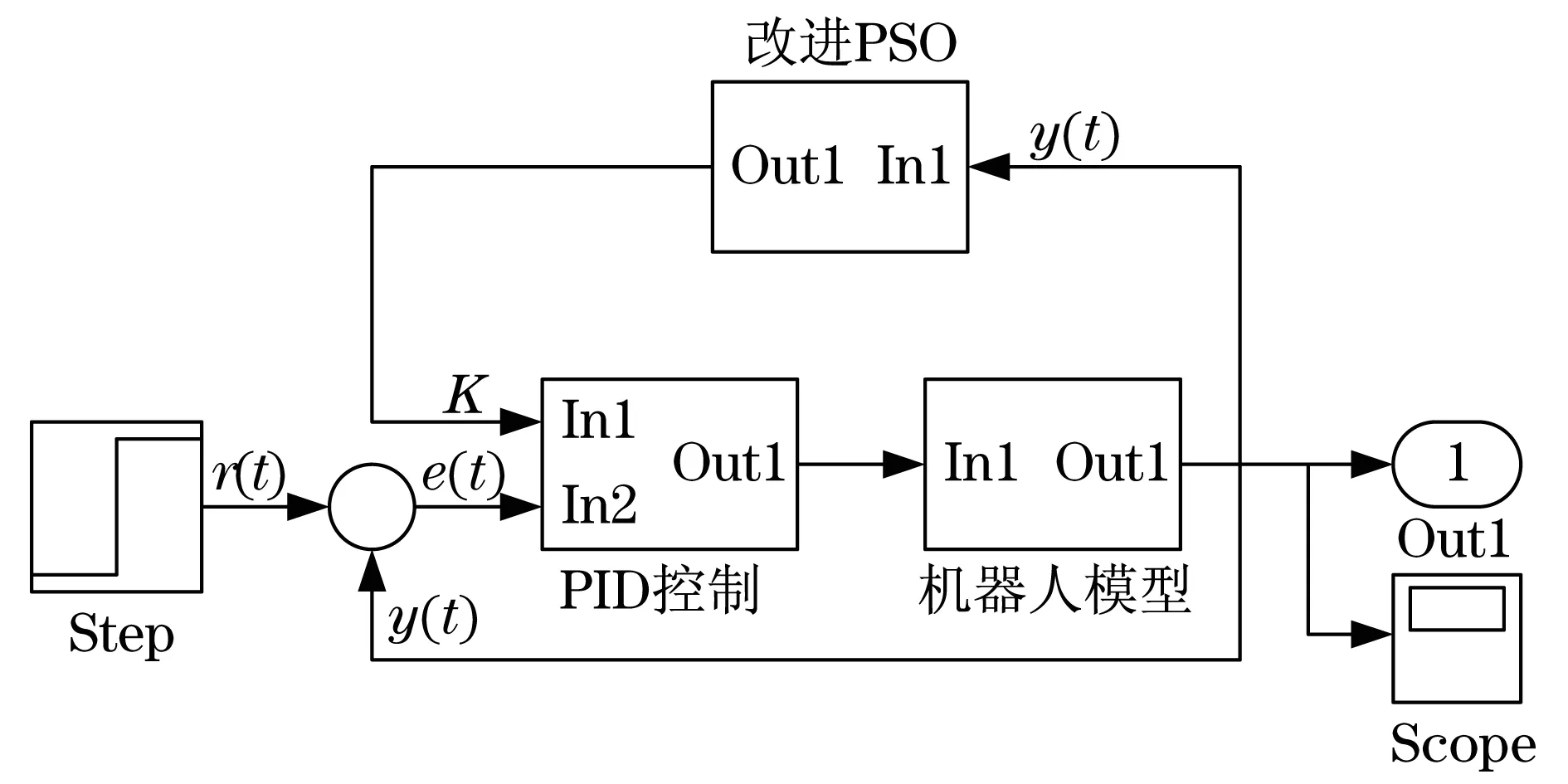
图4 五连杆机器人仿真模型Fig.4 Five-link robot simulation model
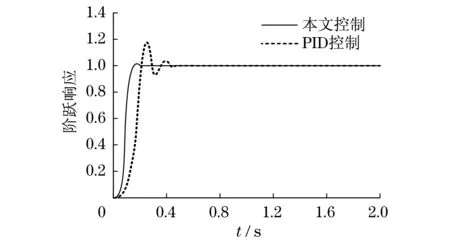
图5 五杆机器人电动机旋转阶跃响应Fig.5 Rotary step response of five-link robot motor
由图5可得:采用常规PID控制器,五连杆机器人电动机旋转阶跃响应速度较慢,大约需要0.5 s才能维持系统稳定输出,上下振荡现象较为严重,导致系统输出误差较大;采用改进PSO分数阶PID控制器,五连杆机器人电动机旋转阶跃响应速度较快,大约需要0.2 s就能维持系统稳定输出,上下振荡现象相对较轻,系统输出误差较小;此优点有利于快速提高系统的稳定性和输出误差.因此,改进PID控制器,适合五杆机器人执行高速度、高精度的定位任务.
5 结语
本文建立了五连杆机器人机构运动简图模型,推导了机构运动的动力学方程式.采用了改进PSO,该算法克服了传统PSO存在的两个主要不足,即收敛速度慢、容易陷入局部最优解.将改进PSO用于调整分数阶PID控制器的参数,针对五连杆机器人操纵器,提出了优化方法来设计最优PID控制器.仿真结果表明:改进PSO可以有效地调节PID控制器的参数,能够快速提高五连杆机器人运动的稳定性,降低系统输出误差.

