推进泵快速启动水力特性及流场演变研究

张富毅，杨 鹏，郑枫川，赵晓阳，刘 影

（1.上海船用柴油机研究所，上海 200090；2.北京理工大学机械与车辆学院，北京 100081）

0 引 言

鱼雷是一种隐蔽性能强、爆破威力大和攻击效果好的水中兵器[1]。空气涡轮泵发射系统是一种常用的鱼雷发射装置[2-3]，其工作原理如图1所示：发射时，打开发射阀，发射气瓶中的高压气体进入涡轮机，驱动其转动，涡轮机带动与海水相连的推进泵快速启动，通过推进泵旋转做功提升海水的压能和动能，并作用在鱼雷尾部，推动鱼雷出管[4]。整个发射过程耗时极短，通常小于1 s，处于强瞬态过程，推进泵是发射系统的关键核心部件，其水力性能的优劣直接决定鱼雷出管的速度、加速度以及出管后的位移等，为实现鱼雷高航速、大深度、远航程和低噪声的目标，有必要深入研究推进泵在快速启动过程中的水力特性及流场演变。

图1 空气涡轮泵发射系统示意图Fig.1 Schematic diagram of air turbopump launching system

国内外学者针对叶片泵的启动过程开展了系列研究。Dazin 等[5-6]提出了叶片泵启动过程中扬程的理论计算方法，并成功预测一台离心泵启动过程中的瞬态扬程；张德胜等[7]也通过混流泵启动试验验证了瞬态扬程理论模型的正确性。Zhang等[8-9]提出水力机械的广义欧拉方程，该方程是由稳定工况的欧拉方程和瞬态过程中所产生的附加理论扬程组成，并指出附加理论扬程由旋转加速扬程和流动惯性扬程两部分组成，同时发现，外特性参数的瞬态变化只与角加速度项有关，而与流动惯性项无关。

Duplaa[10]对离心泵进行了快速启动试验研究，通过瞬时扭矩、流量、进出口压力和转速描述离心泵的运行特性。Wu等[11]搭建了离心泵启动试验台用于研究加速度对瞬态特性的影响，发现以高加速度启动可以较快地达到稳定状态，但是冲击扬程明显增大，并且瞬态性能会因空泡的产生而严重下降。李伟等[12]建立了混流泵启动过程瞬态外特性和压力脉动测量系统，研究不同启动时间和不同流量下瞬态压力脉动特性，结果表明，在启动结束时刻，当流量一定时，压力冲击随启动时间的增加逐渐减弱，当启动时间一定时，进口压力冲击随流量增大逐渐减弱甚至消失，而叶轮中部和出口的压力逐渐增强。陈宗贺[13]采用高速摄影测量方法观测到混流泵启动初期的空化主要由叶顶泄漏涡引起的涡空化和附着在叶片壁面上的附着型空化组成，并随着转速增大，空化区域从叶片压力面中部靠近轮缘处向叶片压力面后缘及轮毂方向发展。李伟等[14]采用数值方法研究了混流泵启动过程进口处的流动特性，发现叶片吸力面流动分离和叶顶间隙泄漏是导致进口回流的主要因素，回流参数随时间呈现先增大后减小的趋势，且主流与回流轴向速度在启动初期呈对称分布。杨敬江等[15]以双蜗壳离心泵为研究对象建立了一套循环管路系统，通过非定常计算发现，在启动初期，蜗壳内部流速变化剧烈，蜗壳入口处存在明显的速度梯度；在启动过程中，隔板初始位置和末端位置的压力脉动幅值相对较大，且隔板外侧的压力脉动相对于隔板内侧更稳定。

综上所述，国内外学者采用理论、试验和数值等方法研究了离心泵和混流泵的启动过程，但是关于轴流式推进泵启动瞬态过程的研究尚未涉及，而轴流式推进泵的几何结构、功能作用和工作环境与常规的离心泵和混流泵相差较大。基于此，本文采用数值模拟方法研究鱼雷发射推进泵在不同启动时间条件下的水力特性以及流场演变，并分析相关流动机理。

1 数值模型及方法

1.1 数值模型

图2为本文所研究的推进泵模型，包含叶轮和导叶两部分，叶轮有6个叶片，导叶有8个叶片。推进泵的主要设计参数为：叶轮直径D=304.8 mm，扬程H=11.9 m，流量Q=580 kg/s，功率为76 kW，转速n=1450 r/min。

图2 推进泵模型Fig.2 Model of propulsion pump

数值计算域如图3 所示，考虑推进泵前后管道和外部水域，外部六面体水域的长宽高分别为30D、10D和20D，入口段管道长为3D，水平出口段管道和竖直出口段管道长为7D。外部水域靠近管道的侧面为壁面，其余5个侧面为开放边界，管道和推进泵叶片均为壁面。不同区域间使用交界面连接，叶轮与入口段、叶轮与导叶之间使用Transient Rotor Interface 交界面，其余使用Stage Average Velocity 交界面。整个装置处于15 m 水深处，环境压力为248 325 Pa，忽略重力因素。

图3 计算域Fig.3 Computational domain

采用结构化网格划分计算域，管道和推进泵的网格如图4所示，在管道和叶片近壁面区布置边界层网格，弯管和推进泵区域进行局部加密。推进泵区域的网格数量直接决定计算的精度和效率，文献[16]对设计工况下的推进泵区域进行了网格无关性分析，最终确定推进泵区域网格数为382 万；管道网格数为143 万，直管段沿流动方向每0.01 m 布置一个节点，弯管段沿流动方向布置90 个节点，即每隔1°布置一个节点，管道圆周方向布置120 个节点，即每隔3°布置一个节点；外部水域网格数为120万，计算域总网格数为645万，网格质量在0.32以上。

图4 网格Fig.4 Mesh

1.2 数值方法

采用雷诺时均方法求解连续性方程和动量方程：

式中，i、j表示笛卡尔坐标方向，x为笛卡尔坐标轴，u为速度，ρ为密度，p为压力，μ和μt分别为层流和湍流黏性系数。

采用SSTk-ω湍流模型，湍动能k方程和湍流频率ω方程[17]分别为

式中，Pk和Pω为湍流生成项，Dk为湍流耗散项，σk和σω2分别为湍动能k和湍流频率ω的普朗特数，F1和F2为混合函数，S为剪切应变率，Cω、βω和α为模型常数。

规定推进泵线性启动，转速变化规律为

式中，ts为启动时间，分别取0.1 s、0.2 s和0.3 s，启动过程分为转速加速和转速稳定两个阶段，总运行时间为0.5 s，三种工况的转速变化规律如图5 所示。计算的时间步长为0.0001 s，每个时间步长内迭代100 步，图6 给出了启动时间为0.2 s 工况的收敛过程，由图可知，整个求解过程残差小于1.5E-4，并且除了最初小段时间外，其余时间残差均小于1E-4，计算精度满足工程要求。

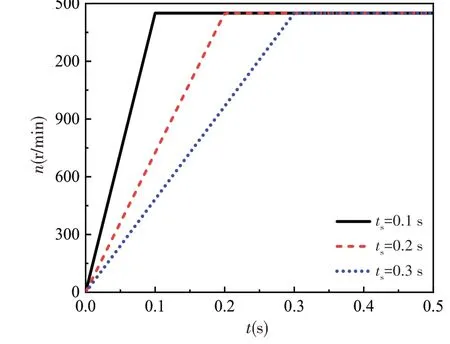
图5 转速变化规律Fig.5 Variation of rotational speed

图6 收敛过程Fig.6 Process of convergence

文献[18]采用上述数值方法计算得到不同流量下推进泵的外特性参数，并与试验数据对比，结果表明，推进泵扬程系数、功率系数和效率的数值结果与试验数据吻合良好，表明上述数值计算方法可以准确预测推进泵外特性。文献[13]对比了混流泵启动过程瞬态流场的数值结果和高速摄像测量结果，两者吻合度良好，表明瞬态数值方法可以准确描述泵内流场演变，而本文的数值方法与文献[13]一致，可间接说明本文数值研究的可靠性。

2 结果分析

2.1 水力特性分析

图7给出了流量的演变历程，由图可知，流量随时间持续增加，当转速增大至稳定值后，流量并未达到稳定值，而是继续增大；整个过程中，启动时间越小，流量越大，当运行至0.5 s 时，启动时间为0.1 s、0.2 s和0.3 s时的流量分别为311.04 kg/s、290.61 kg/s和268.98 kg/s，分别是0.536倍、0.501倍和0.464倍设计流量；而在加速结束瞬间，启动时间为0.1 s、0.2 s和0.3 s时的流量分别为56.03 kg/s、100.54 kg/s和139.46 kg/s，启动时间越小，流量越小，相对于转速变化，滞后程度越强。

图7 流量演变历程Fig.7 Variation of flow rate

由动量定理可知，推力是由流量决定的，所以推力的变化趋势与流量变化趋势类似，如图8所示，推力持续增加，整个过程中，启动时间越小，推力越大，当运行至0.5 s时，启动时间为0.1 s、0.2 s和0.3 s时的推力分别为2394.25 N、2089.91 N和1790.54 N，而在加速结束瞬间的推力分别为77.64 N、250.07 N和481.17 N。

图8 推力演变历程Fig.8 Variation of thrust

图9给出了推进泵进出口压力的演变历程，Pin0.1、Pin0.2和Pin0.3分别表示启动时间为0.1 s、0.2 s和0.3 s时的进口压力，Pout0.1、Pout0.2和Pout0.3分别表示启动时间为0.1 s、0.2 s和0.3 s时的出口压力。由图可知，启动瞬间，进出口压力相同，均为环境压力；随后进口压力先减小后增大，最小值分别为-84.18 kPa、60.91 kPa 和123.43 kPa，最小值随启动时间增加而增大；出口压力先增大后减小，最大值分别为596.75 kPa、520.85 kPa和466.28 kPa，最大值随启动时间增大而减小；经过0.5 s的运行，三种工况下的进出口压力基本一致。进一步分析发现，三种工况下，出口压力均是在加速结束瞬间达到最大值，而进口压力均是在加速完成之前就达到最小值；此外，当启动时间为0.1 s时，进口处压力的最小值远低于水的饱和蒸汽压，说明在推进泵入口处产生大量的空泡，出现严重的空化现象。

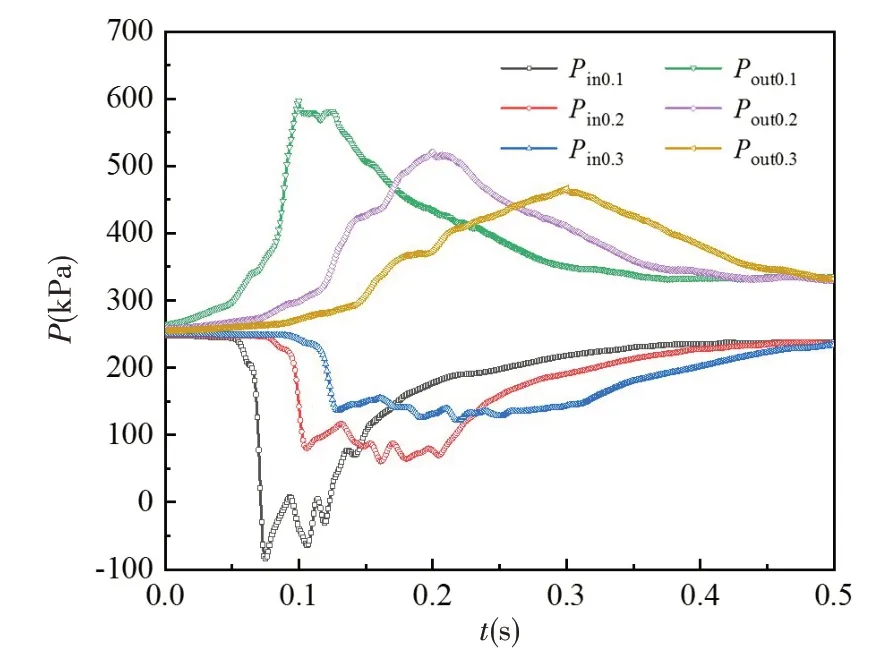
图9 进出口压力演变历程Fig.9 Variation of inlet and outlet pressures

图10 给出了扬程的演变历程，扬程主要是由推进泵出口压力决定的，所以其变化趋势同出口压力变化趋势基本一致，在叶轮加速过程中，快速增大，加速完成后，持续减小，并在加速完成瞬间，存在远大于设计扬程的冲击扬程，启动时间为0.1 s、0.2 s 和0.3 s 时的冲击扬程分别达到了65.06 m、45.41 m和33.03 m，冲击扬程随启动时间增大而减小，与出口压力变化规律一致。

图10 扬程演变历程Fig.10 Variation of head

图11、图12 和图13 分别给出了叶轮轴向力、轴向力矩和功率的演变历程。由图可知，轴向力、轴向力矩和功率的变化趋势基本一致，叶轮加速过程中，轴向力、轴向力矩和功率快速增大，加速完成之后，轴向力、轴向力矩和功率持续减小。在加速结束瞬间三者均达到最大值，启动时间为0.1 s、0.2 s和0.3 s 时轴向力最大值分别为9058.53 N、8730.26 N 和7612.23 N，轴向力矩最大值分别为668.39 N·m、643.41 N·m 和567.37 N·m，功率最大值分别为101.46 kW、97.70 kW 和86.13 kW，轴向力、轴向力矩和功率的最大值均远大于推进泵的设计值，并且均随着启动时间的增大而减小，说明以较高的角加速度启动推进泵时，叶轮所受到的水流冲击作用加重。

图11 轴向力演变历程Fig.11 Variation of axial force

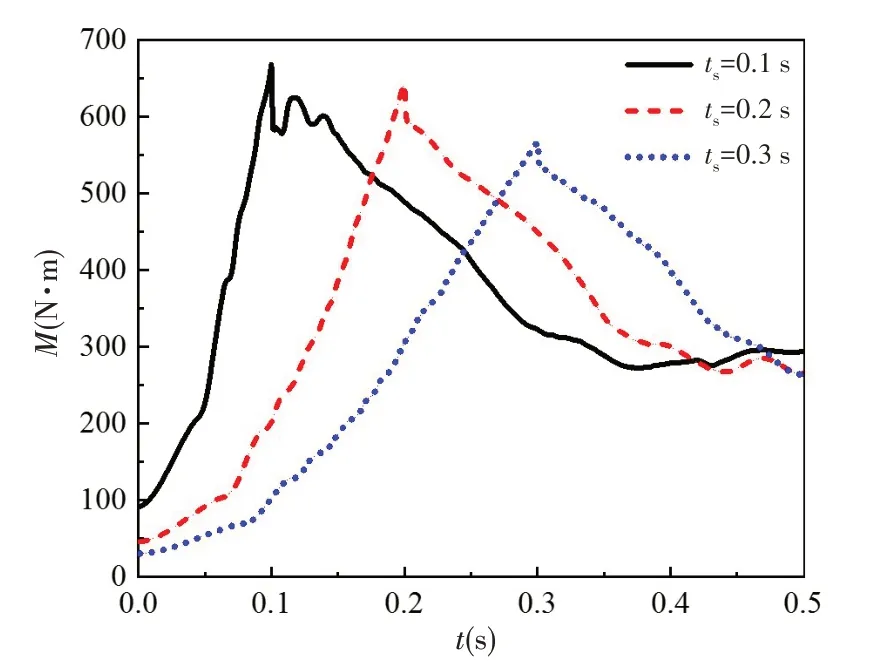
图12 轴向力矩演变历程Fig.12 Variation of axial moment

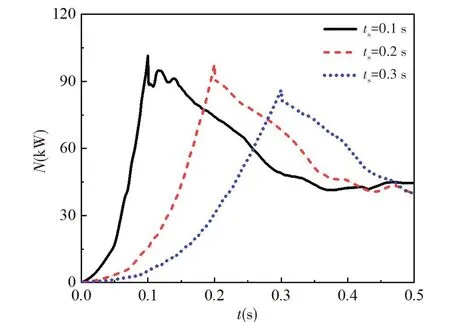
图13 功率演变历程Fig.13 Variation of power

图14 给出了效率的演变历程。由图可知，推进泵效率持续增大最终达到相对稳定值，运行至0.5 s时，启动时间为0.1 s、0.2 s和0.3 s时的效率分别为67.98%、68.54%和66.23%。

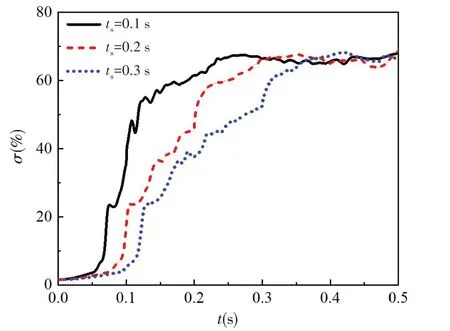
图14 效率演变历程Fig.14 Variation of efficiency

2.2 流场演变分析

图15、图16和图17分别为叶轮区域10%、50%和90%叶高展向平面流线分布。由图可知，在运行初期，叶轮前缘存在强烈的来流冲击，叶轮通道间产生了严重的流动分离和漩涡结构，而叶轮尾缘出现明显的回流现象，随着时间的推移，流动逐渐趋于稳定。对比不同启动时间的10%和50%叶高展向流线分布可以发现，启动时间越短，流场越快达到稳定状态；当ts=0.1 s，运行至0.3 s时，漩涡结构基本消除；当ts=0.2 s，运行至0.4 s 时，漩涡结构基本消除；而当ts=0.3 s，运行至0.5 s 时，漩涡结构才基本消除。由于90%叶高平面靠近叶顶位置，流动极其复杂且不稳定，即使运行至0.5 s时，依然存在流动分离、漩涡结构和回流现象，说明推进泵内部依然未达到稳定的流动状态。

图15 叶轮区域10%展向表面流线分布Fig.15 Distribution of streamline on 10%span surface of impeller

图17 叶轮区域90%展向表面流线分布Fig.17 Distribution of streamline on 90%span surface of impeller

图18为导叶区域轴向平面上的轴向速度分布，其中轴向速度取负值表示该区域产生了回流。由图可知，当ts=0.1 s，运行至0.1 s时，转速已经达到最大转速，但此时入口、中间和出口平面均存在大面积的回流区域；运行至0.2 s 时，三个平面内的回流区域开始减小；当运行至0.5 s 时，入口和出口平面内的回流区域基本消除，而中间平面靠近导叶叶片区域依然存在小面积的回流区域。当ts=0.2 s，运行至0.1 s时，转速还未达到最大值，三个平面内轴向速度较小，且仅在入口平面存在小面积回流区域；运行至0.2 s时，转速达到最大值，三个平面内均出现大面积回流区域，随后回流区面积逐渐减小；运行至0.5 s时，也仅中间平面靠近导叶叶片区域存在小面积的回流区域。当ts=0.3 s，运行至0.1 s时，转速处于较低水平，轴向速度基本为0且无回流区，运行至0.1 s时，三个平面开始出现较为明显回流区域；运行至0.3 s时，回流区面积达到最大值，随后逐渐减小，而当运行至0.5 s时，轴向速度分布规律与ts=0.1 s和ts=0.2 s时类似。

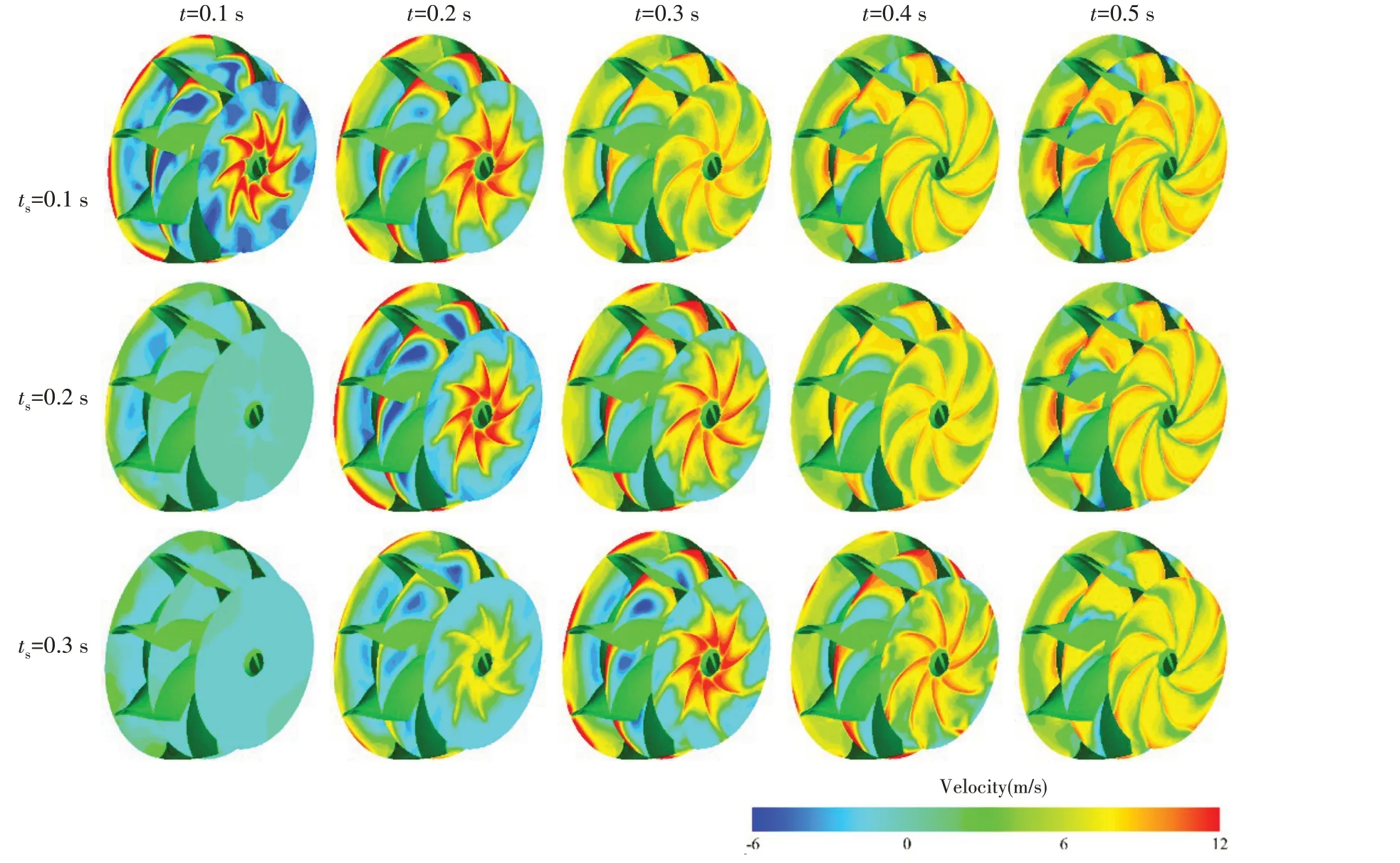
图18 导叶区域轴向平面速度分布Fig.18 Distribution of axial velocity on axial plane of guide vane

3 结 论

本文采用数值模拟方法研究了鱼雷发射推进泵启动过程中的水力特性和流场演变情况，主要结论如下：

（1）在推进泵启动过程中，流量和推力随时间持续增加，扬程、轴向力、轴向力矩和功率随时间先增大后减小，效率随时间先增大后保持稳定。扬程、轴向力、轴向力矩和功率在加速结束瞬间存在极大值，且极大值随着启动时间的增大而减小。

（2）启动初期，叶轮区域存在严重的来流冲击、流动分离和漩涡结构，导叶区域的入口、中间和出口平面存在大面积回流区域，随着时间推移，流场逐渐趋于稳定。启动时间对推进泵流场演变具有显著影响，启动时间越小，流场越快达到稳定状态。

（3）为提高鱼雷出管速度，并且保证推进泵在启动过程中无空泡产生以及内部流场以较快时间运行至稳定状态，建议以0.2 s启动时间启动推进泵。