物体脱离轨道瞬间的速度分析

蔡 飞

(江苏省常熟市伦华高级中学,江苏 常熟 215500)

高中物理对于动力学中关于力和运动、功能关系的研究,通常会在有预设轨道中来进行运动的分析和讨论.而且预设轨道中,往往会涉及固定轨道和动态轨道两种情况.对于不同的模型,讨论的方向会有所不同.本文重点研究物体在不同条件下脱离轨道瞬间的速度问题.

1 有约束作用下的固定轨道脱离分析

有约束作用下的固定轨道,即物体的运动轨迹只能沿轨道,通常研究的为小环套嵌于轨道上或小球在有内外轨的轨道中的运动模型.下面将对小环在轨道上的运动脱离速度问题进行分析.

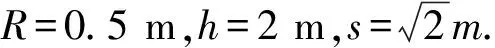
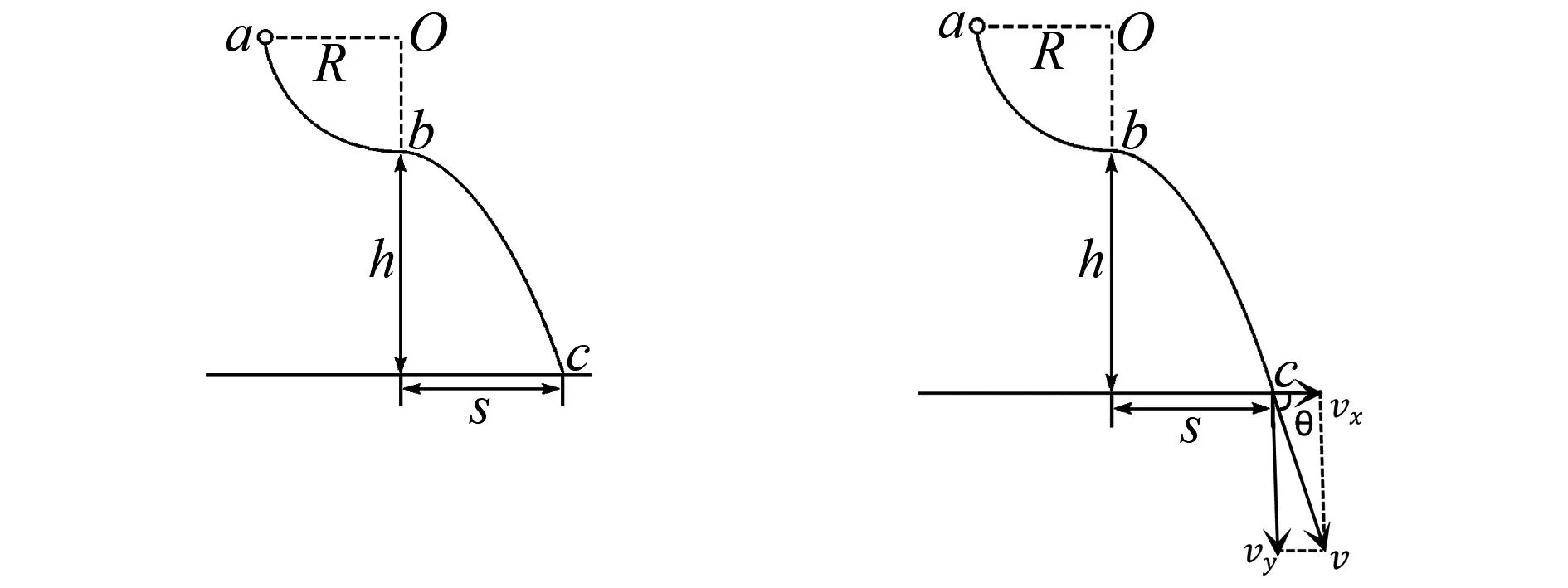
图1 例1题图

1.1 模型分析法

如图2,bc段为以b为顶点的抛物线,显然bc段轨道对应某一平抛运动的轨迹.下面先求出bc段轨道对应的平抛运动.设初速度为v0,c点速度方向与水平方向夹角为θ.由平抛运动知识可得:

至此,此抛物线对应的平抛运动原型已确定.接下来对给定条件结合平抛运动原型进行分析.

当R=0.5 m时,小环从a到c,由机械能守恒可得:

∵小环从c点飞出时速度方向沿曲线在c点的切线方向

1.2 轨迹分析法

对于轨道为抛物线的物理模型,可以从运动原型入手,通过运动原型的分析,确定轨道上任意一点的速度方向,从而求解速度水平分量和竖直分量.此外,抛物线也是比较典型的几何模型,所以处理抛物线轨道的问题时,也可以利用数学方法去解决.因为物体在固定轨道上运动,任意一点的速度方向为切线方向,所以可以通过建立数学模型,结合导数的方法求解抛物线在任意一点的斜率,从而确定切线方向[2].

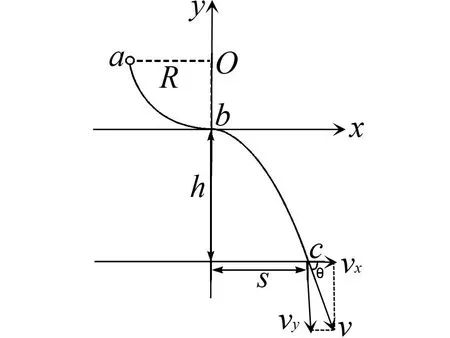
图3 轨迹分析法示意图

如图3所示,以b为坐标原点,水平方向为x轴,竖直方向为y轴建立

直角坐标系.易得bc的抛物线解析式为:

y=-x2∴y′=-2x

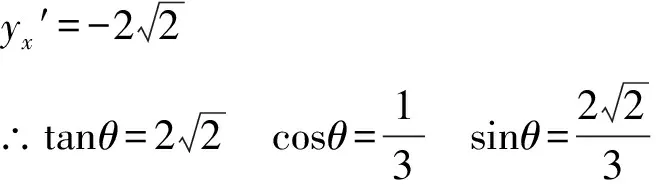
物体从a到c,由机械能守恒可得(R=0.5m):

∵小环从c点飞出时速度方向沿曲线在c点的切线方向

显然特定曲线的轨道原型的问题中,利用轨迹分析也能较好地解决.

点评本例中讨论的轨道为抛物线轨道,由于抛物线都有对应的抛体运动,所以在分析问题中可以从抛物线对应的抛体运动原型入手,通过对抛体运动的特征来确定抛物线的轨迹特点,对于抛物线而言此法比较实用.但其他轨道难以匹配合适的运动,也可以从轨迹的几何性质入手,通过数学方法对轨道的切线和法线进行分析,从而确定运动的性质.

2 无约束作用下的固定轨道脱离分析

无约束作用下的固定轨道的运动,即物体在轨道内侧或外侧发生运动,在运动过程中因不受约束,当不满足轨道运动条件时物体会脱离轨道.下面以小球在轨道内侧的运动进行脱离速度的分析.

例2如图4所示,半径为R的半圆型轨道竖直固定在水平地面上.质量为m的小球以初速度v0向右运动冲上竖直半圆轨道,所有接触面均光滑,不计空气阻力,讨论小球脱离轨道的速度.

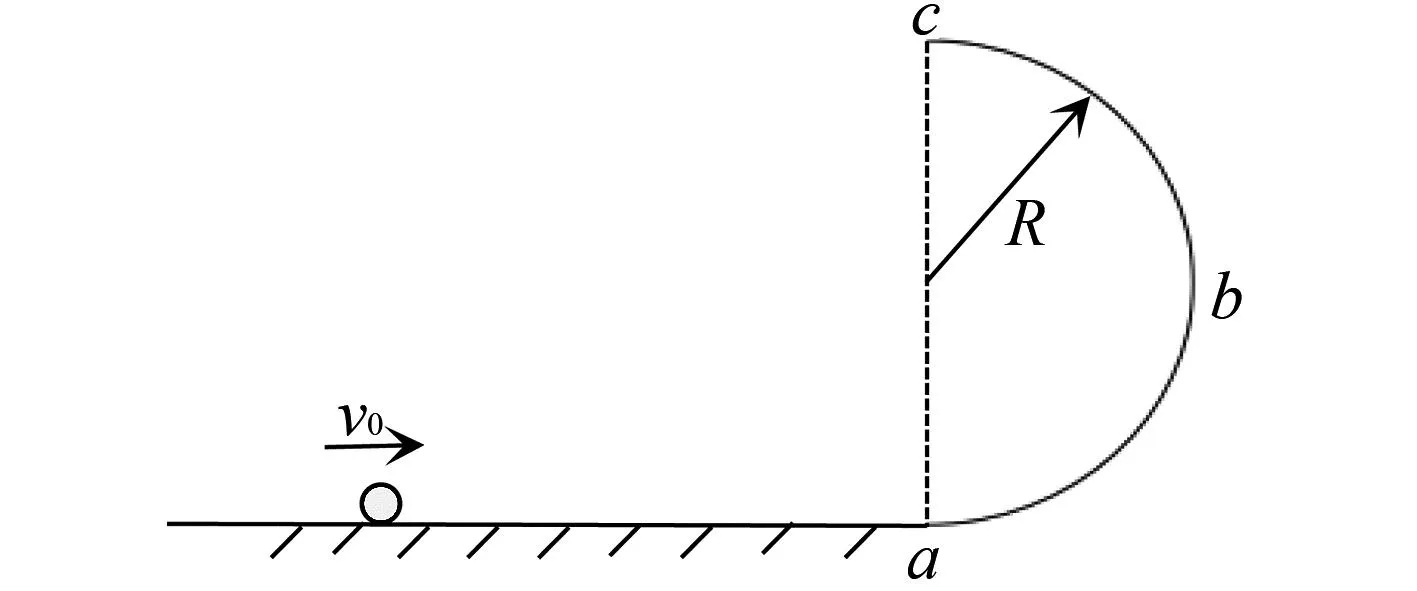
图4 例2题图

分析小球脱离轨道分三种情况:

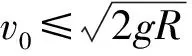
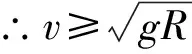
方向水平向左.脱离后物体做平抛运动.

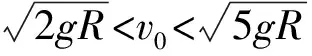
①

从a点到脱离轨道有机械能守恒定律可得:

②

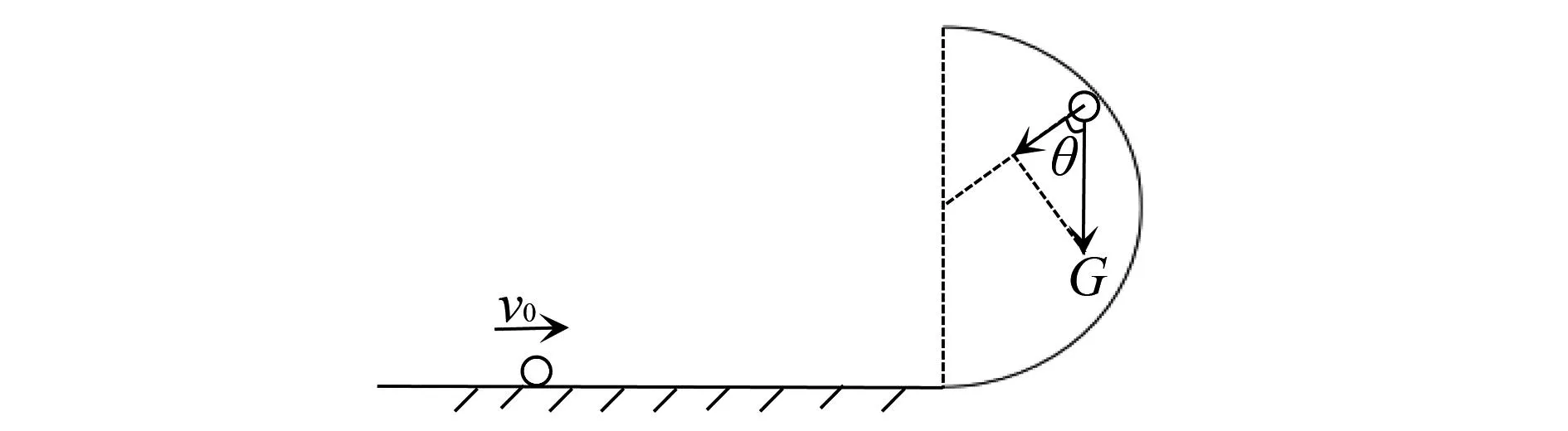
图5 第三种情况示意图

小结物体在有、无约束条件下的固定轨道运动脱离时,物体的速度方向始终沿切线方向,分析脱离速度的过程中可以从运动原型入手,也可以借助数学方法寻找切线,同时还可以结合受力的特点研究物体的速度.对于固定轨道而言,物体脱离速度沿切线方向.那么是不是意味着所有的轨道运动的脱离速度都是沿切线方向呢?答案显然是否定的.物体脱离动态轨道的运动中,脱离速度的方向一般不沿切线方向,而是相对速度的方向沿切线方向.接下来重点探究物体脱离动态轨道的速度问题.

3 运动轨道脱离分析

3.1 物体与轨道发生相对运动时的脱离速度研究

图6 例3题图

例3如图6所示,质量为m的凹槽置于水平面上,凹槽弧形是半径为R的圆轨道的一部分,图中θ=60°.一质量为m的小球在A点正上方高度为R处由静止释放,所有接触面均光滑,不计空气阻力,求小球飞离凹槽瞬间的水平速度和竖直速度.

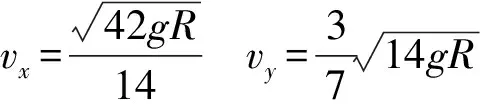
点评在动态轨道上运动的物体,由于轨道速度不为零,物体的脱离速度方向不沿切线方向,而是相对轨道的速度沿切线方向.动态轨道问题往往会与动量守恒的问题相结合,轨道速度为水平方向.所以处理此类问题时,一般会设定物体的速度的水平分量和竖直分量,通过相对速度与竖直速度的合速度沿轨道切线方向来解决问题.

3.2 物体与轨道发生相对运动时的脱离速度应用

图7 变式1图

变式1如图7所示,质量为m的小球从凹槽上方h的高度自由释放,凹槽的质量也为m.求小球飞离凹槽瞬间的速度.所有接触面均光滑,不计空气阻力.

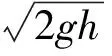
变式2如图8所示,光滑的水平面上固定平行导轨PQ、MN,两导轨之间的距离为2R.一质量为m光滑凹槽置于平行导轨之间,凹槽弧形部分为半圆形,且半径为R.现一质量为m小球以v0向左运动,所有接触面均光滑,不计空气阻力,求小球运动到凹槽b点时的速度.

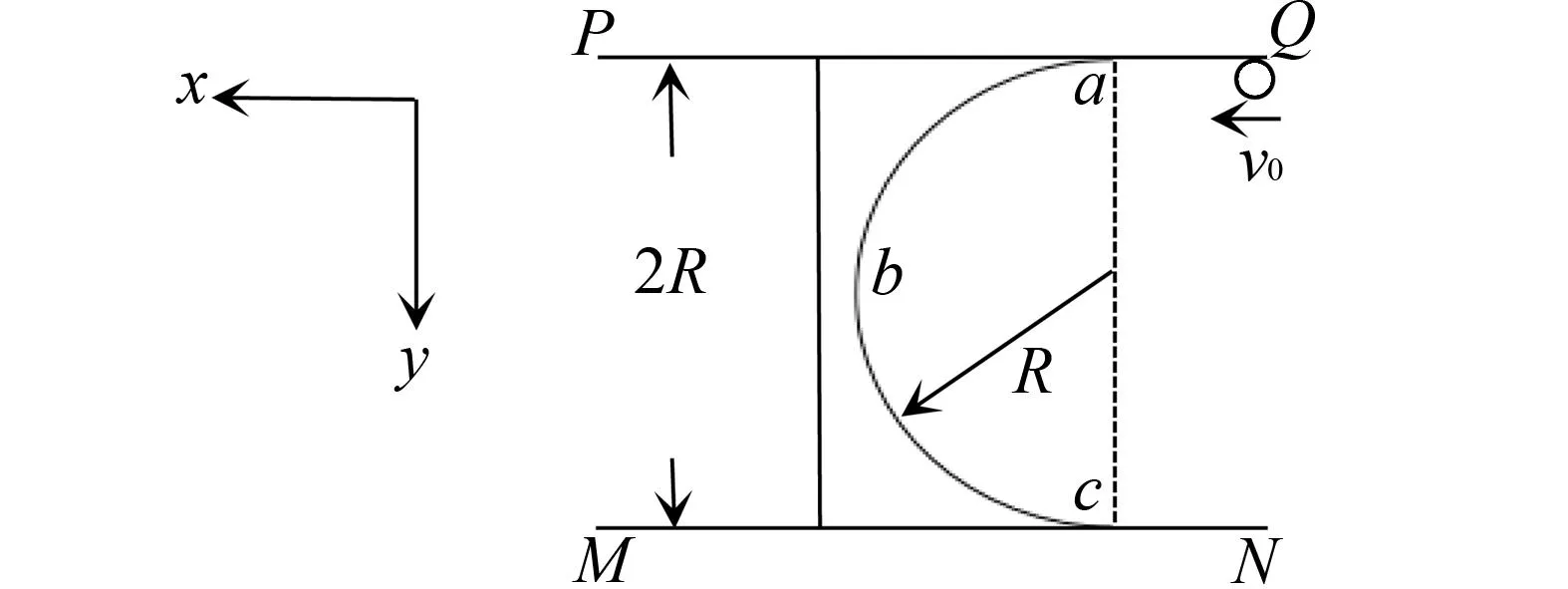
图8 变式2图

变式3如图9,曲边形abcd由两段半径为R,圆心角为60°的扇形和线段bc构成,其质量为m,一质量也为m小球以v0=3 m/s的速度向右运动,冲上曲面体abcd,试分析小球从b点飞离后能否落在bc段.若能,求出落点到b的距离,若不能,分析原因.已知R=0.1 m,xbc=0.4 m.所有接触面均光滑,不计空气阻力.

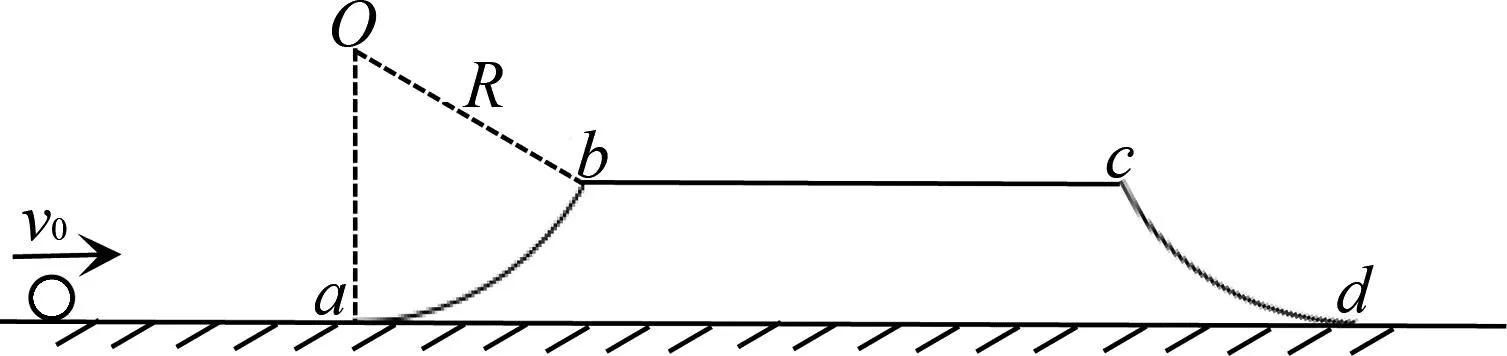
图9 变式3图

4 结束语

物体在有、无约束的固定轨道上运动时,脱离瞬间的速度沿切线方向.在运动轨道上的脱离速度则是相对速度的方向为切线方向,所以在研究脱离速度的问题时,首先要确定的是轨道是否固定.

不论是固定轨道还是动态轨道,物体脱离速度相对于轨道都是沿切线方向,在这点上,不同类型的轨道运动脱离速度都是统一的.