一元三次方程韦达定理及其应用
刘海涛
(1.安徽省芜湖市第一中学,安徽 芜湖 241000;2.新青年数学教师工作室,安徽 芜湖 241000)
在教学中笔者发现,在高中数学联赛或一些高校的强基考试中,经常会出现对一元三次方程的韦达定理的考查,甚至在一些省、市的高考模拟卷中也偶有考查.但是学生对此知识点知之甚少(该定理不属于高中教材内容),少部分学生虽知道该定理却不会应用,导致普遍对涉及该定理的问题望而生畏、望而却步,从而被动放弃,实在可惜.笔者通过梳理近些年的相关考题,在介绍一元三次方程的韦达定理的基础上,从该定理在不同问题上的应用予以分类,整理成文,以供读者学习、交流之用,以期抛砖引玉[1].
1 定理的介绍
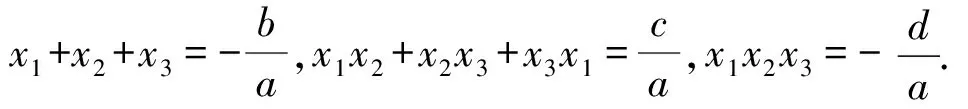
证明由a(x-x1)(x-x2)(x-x3)=a[x3-(x1+x2+x3)x2+(x1x2+x2x3+x3x1)x-x1x2x3],得
-a(x1+x2+x3)=b,
a(x1x2+x2x3+x3x1)=c,
-ax1x2x3=d,
化简得证.
说明该定理是在复数域内,即三个根(x1,x2,x3)可为实数也可为虚数.
2 定理的应用
2.1 在三次方程中的直接应用
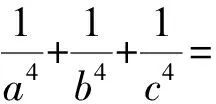
解析由韦达定理得a+b+c=3,ab+bc+ca=-2,abc=-1,则
=a4b4+b4c4+c4a4
=(a2b2+b2c2+c2a2)2-2(a4b2c2+a2b4c2+a2b2c4)
=[(ab+bc+ca)2-2abc(a+b+c)]2-2a2b2c2[(a+b+c)2-2(ab+bc+ca)]=74.
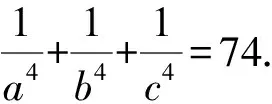
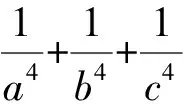
2.2 在函数问题中的应用
2.2.1求函数的解析式
例2设α,β,γ为方程x3-x+1=0的三个实根,求一个三次项系数为1的三次函数f(x),使方程f(x)=0的三根分别为1+α2,1+β2,1+γ2.
解析由韦达定理,得α+β+γ=0,αβ+βγ+γα=-1,αβγ=-1,则
α2+β2+γ2=2,(αβ)2+(βγ)2+(γα)2=1.
不妨设f(x)=x3+ax2+bx+c,则
a=-[(1+α2)+(1+β2)+(1+γ2)]=-5,
b=(1+α2)(1+β2)+(1+β2)(1+γ2)+(1+γ2)(1+α2)=8,
c=-(1+α2)(1+β2)(1+γ2)=-5.
故f(x)=x3-5x2+8x-5.
评注该题为2021年天津大学强基考题,该题实为考查一元三次方程韦达定理的正向、逆向使用.
2.2.2研究三次函数零点的关系
例3 已知函数f(x)=x(x-3)2,若存在f(a)=f(b)=f(c),a A.1 C.a+b>2 D.abc∈(0,4) 解析求导得f′(x)=3(x-1)(x-3). 易知f(x)在(-∞,1)和(3,+∞)上单调递增,在(1,3)上单调递减,极小值f(3)=0,极大值f(1)=4. 设f(a)=f(b)=f(c)=k,易知k∈(0,4),a∈(0,1),b∈(1,3),不难判断出函数f(x)在区间(0,3)上属于极值点左移,有a+b>2. 由f(x)=k得方程x3-6x2+9x-k=0,其中a,b.c为该方程三个根. 由韦达定理得a+b+c=6,abc=k∈(0,4). 故选BCD. 评注该题为2023年深圳市一模考题的11题,网上有深圳市老师反映该题得分率较低,多数学生不知道如何判断B,D两选项的正确与否,少部分学生答对也是靠对函数图象的直观性做出的猜测.事实上,若考生考前了解过一元三次方程的韦达定理,则可较为快速、准确地解出该题. 2.2.3求函数的最小值 解析设方程x3-ax2+bx-a=0的三个正实根分别为α,β,γ,则 α+β+γ=αβγ=a,αβ+βγ+γα=b. 由三元均值不等式,得 由(α+β+γ)2≥3(αβ+βγ+γα),得a2≥3b. 评注该题为2020年第十届中国东南地区数学奥林匹克考试第1天的第1题.作为一项重大竞赛考题,该题的难度偏小,主要考查一元三次方程的韦达定理和两个三元不等式,是一个可以轻松“拿分”的数学竞赛考题. 例5 求下列三式的值: (1)cos40°+cos80°+cos°160°; (2)cos40°cos80°+cos80°cos160°+cos160°·cos40°; (3)cos40°cos80°cos160°. 于是得到 (1)cos40°+cos80°+cos160°=0; 评注该题为华东师范大学出版社出版的《数学奥林匹克小丛书》上的一道题,解答该题的关键在于数系一元三次方程的韦达定理的三式结构特征,以及三倍角余弦公式. 例6 已知a,b,c∈Z,且a+b+c=0,求证:2(a4+b4+c4)是一个完全平方数. 证明构造方程x3+mx2+nx+k=0(m,n,k∈Z),其中a,b,c是该方程的三个整数根,由韦达定理得m=0,n=ab+bc+ca,k=-abc. 由方程得a3=-(na+k),b3=-(nb+k),c3=-(nc+k). 所以2(a4+b4+c4)=-2n(a2+b2+c2)-2k(a+b+c)=-2n[(a+b+c)2-2(ab+bc+ca)]=(2n)2,是一个完全平方数. 评注该题对高中数学竞赛生来说,是一道很平常的数论练习题,方法也有很多,但是利用一元三次方程(这里是整数域下的三次方程)的韦达定理解题,能起到事半功倍的效果,给人耳目一新的感觉[2]. 例7 已知三个复数a,b,c的模均为1,且a+b+c=1,abc=1,求a,b,c. 所以ab+bc+ca=abc=1. 由此可得a,b,c为方程x3-x2+x-1=0的三个根,因式分解方程可得(x-1)(x2+1)=0. 故{a,b,c}={1,i,-i}. 例8 设a,b,c是实数,方程x3+ax2+bx+c=0有三个正根,证明:2a3+9c≤7ab,并且等号成立当且仅当这3个正根相等. 证明设题中方程的三个正根分别为α,β,γ,由韦达定理,得 α+β+γ=-a,αβ+βγ+γα=b,αβγ=-c. 2a3+9c-7ab=-2(α+β+γ)3-9αβγ+7(α+β+γ)(αβ+βγ+γα)=(α+β+γ)[7(αβ+βγ+γα)-2(α+β+γ)2]-9αβγ=(α+β+γ)[3(αβ+βγ+γα)-2(α2+β2+γ2)]-9αβγ=(α2β+αβ2+β2γ+βγ2+γ2α+γα2)-2(α3+β3+γ3)=-(α3+β3-α2β-αβ2)-(β3+γ3-β2γ-βγ2)-(γ3+α3-γ2α-γα2)=-(α+β)(α-β)2-(β+γ)(β-γ)2-(γ+α)(γ-α)2≤0,当且仅当α=β=γ时取等号,故得证. 评注该题是2014年北京大学夏令营考题,利用韦达定理将2a3+9c-7ab转化为关于三正根α,β,γ的表达式,代数化简即可得证. 例9 已知长方体的体积为1,长、宽、高之和为k,表面积为2k,求实数k的取值范围. 解析设该长方体的长、宽、高分别为a,b,c,则a+b+c=k,ab+bc+ca=k,abc=1,则可将a,b,c视作方程x3-kx2+kx-1=0的三根. 又该方程可因式分解为(x-1)[x2-(k-1)x+1]=0,不妨设a=1,则b,c是方程x2-(k-1)x+1的两根. 评注题中三个条件恰好得到一元三次方程的韦达定理式的三个结构式,自然将长、宽、高作为一元三次方程的三根,借助三次方程解题. 例10 已知△ABC的三边分别为a,b,c,周长为2,求证:a2+b2+c2+2abc<2. 证明由题知a+b+c>2c,易得0 不等式a2+b2+c2+2abc<2等价于a2+b2+c2+2abc 设f(x)=(x-a)(x-b)(x-c),化简得 f(x)=x3-2x2+(ab+bc+ca)x-abc. 问题等价于证明f(1)>0. 而由a,b,c∈(0,1),得证f(1)=(1-a)(1-b)(1-c)>0. 评注对于ab+bc+ca>1+abc的证明,解法多样,但是利用一元三次方程的韦达定理解题却是最简便的. 一元三次方程的韦达定理虽没有出现在教材中,也不属于高中数学的知识点,但是通过文中的推导,我们不难发现,对于高中生而言该定理的理解完全不成问题,可以作为一种新定义题来命制题目,来考查学生的逻辑推理、数学运算等数学能力.基于此,笔者认为,在日常的教学中,广大一线教师可以考虑介绍一些介于高中与大学之间的数学知识,尤其是从数学逻辑推理的角度予以介绍,并给出证明过程,并辅之适量的习题以供训练,这样,学生的数学思维能力和知识储备都将得到大幅提升,高考中的优势自然明显,将来的数学学习也必将顺利.在介绍教材之外的知识点时,更重要的是让学生亲历知识的生成过程,知道概念的由来、定理的具体推导,从而掌握其中蕴含的数学思想方法[3],这样,在遇到一道陌生问题时,学生才具有分析问题、解决问题的能力,考试自然能取得理想的成绩[4].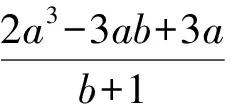


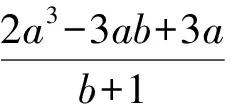
2.3 在三角函数求值中的应用
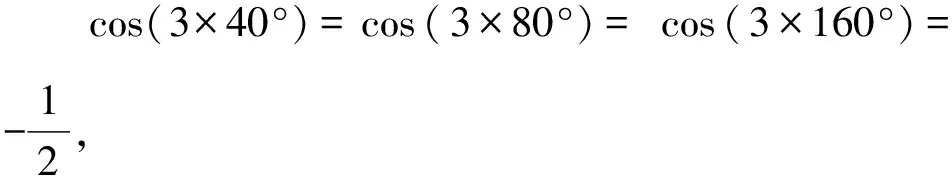
2.4 在数论问题中的应用
2.5 在复数问题中的应用
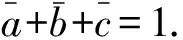

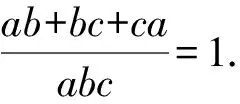
2.6 在不等式问题中的应用
2.7 在立体几何中的应用
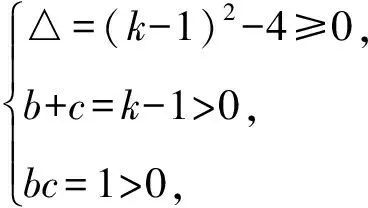
2.8 在三角形中的应用
3 结束语

