例谈导数与三角函数的“联姻”
林国红
(广东省佛山市乐从中学 ,广东 佛山 528315)
新高考已经不仅仅局限于基本知识和基本技能的考查,更重视对学生综合核心素养和关键能力的考查,题目会更加灵活多变,富有创新性和综合性.在题目中融入数学文化、生活实际、跨学科的知识,将不同的知识融合交汇,那么知识之间的融合必然会更加精彩.
三角函数有其独特的性质,当导数与三角函数“联姻”时,三角函数的周期性、有界性等就被融入进来.对于三角函数的单调性、奇偶性、对称性、最值问题、含参问题或者相关综合性问题,借助导数进行研究能更充分地考查数学思想方法、运算求解能力、综合应变与解题调控能力,也能很好地彰显考生解题方法的灵活性、多样性,从而备受命题者的青睐,不少高考试题和模拟试题均在三角函数和导数交汇处进行命题.下面笔者以近年高考或模考中与三角函数有关的导数题为例,进行分类归纳与解答,供大家参考.
1 三角函数与多项式函数组合
例1 已知函数f(x)=ax-sinx(a∈R).
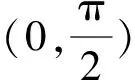
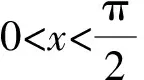
解析(1)由已知,得f′(x)=a-cosx.
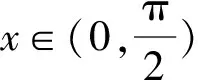
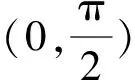
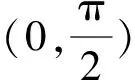
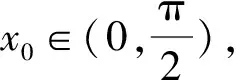
综上,a的取值范围为(0,1).
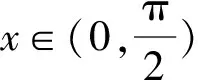
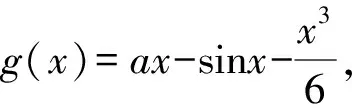
=a-1.
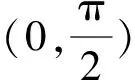
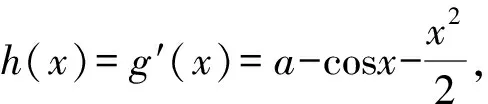
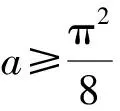
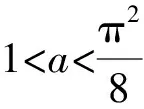
综上,a的取值范围是(-∞,1].
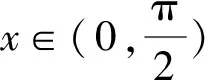
2 三角函数与对数型函数组合
例2 (2019年全国Ⅰ卷理20)已知函数f(x)=sinx-ln(1+x),f′(x)为f(x)的导数.

(2)f(x)有且仅有2个零点.
解析(1)设g(x)=f′(x),则
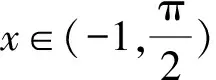
则当x∈(-1,α)时,g′(x)>0;
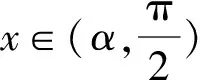


(2)易得f(x)的定义域为(-1,+∞).
①当x∈(-1,0]时,由(1)知,f′(x)在(-1,0)单调递增,而f′(0)=0,所以当x∈(-1,0)时,f′(x)<0,故f(x)在(-1,0)单调递减.又f(0)=0,从而x=0是f(x)在(-1,0]的唯一零点.
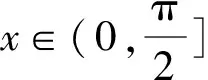
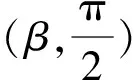

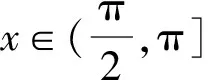
④当x∈(π,+∞)时,ln(x+1)>1,所以f(x)<0,从而f(x)在(π,+∞)没有零点.
综上,f(x)有且仅有2个零点.

3 三角函数与指数型函数组合
例3 已知函数f(x)=exsinx.
(1)求f(x)的单调递减区间;
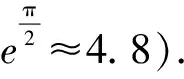
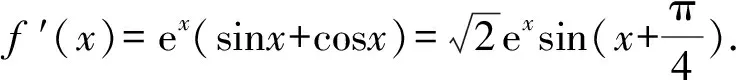



(2)由已知g(x)=exsinx-ax,
所以g′(x)=ex(sinx+cosx)-a.
令h(x)=g′(x),则h′(x)=2excosx.
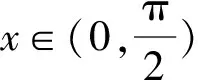
又g′(0)=1-a,
g′(π)=-ex-a<0,

所以当x∈(0,x0)时,g′(x)>0,
当x∈(x0,π)时,g′(x)<0.
所以g(x)在(0,x0)上单调递增,在(x0,π)上单调递减.
因为g(0)=0,所以g(x0)>0.
又g(π)=-aπ<0,则由零点存在性定理可得,此时g(x)在(0,π)上仅有1个零点.
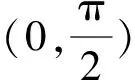
因为g(0)=0,所以g(x1)<0.
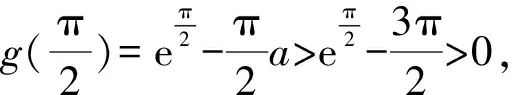
所以g(x2)>0.
又因为g(π)=-aπ<0,由零点存在性定理可得,g(x)在(x1,x2)和(x2,π)内各有1个零点,即此时g(x)在(0,π)上有2个零点.
综上所述,当0 评注本题难点在于研究函数g(x)的零点.函数的零点多与单调性有关,一般利用导数得到函数的单调区间,由于一阶导函数比较复杂,故求二阶导函数,通过研究y=g″(x)图象的大致特征,确定参数a的分界点,再结合零点存在性定理分析.与三角函数单调性有关的题目,两次求导的处理方法较为常见. 例4 (2019年泰安二模21)已知函数f(x)=(x-m)lnx(m≤0). (1)若函数f(x)存在极小值点,求m的取值范围; (2)证明:f(x+m) 解析(1)m的取值范围是(-e-2,0]. (2)当m≤0时,有 f(x+m)=xln(x+m)≤xlnx, 若xlnx 则f(x+m) ①若x∈(0,1],则ex+cosx-1>0,xlnx≤0. 于是xlnx 所以f(x+m) ②若x∈(1,+∞),令 h(x)=ex+cosx-1-xlnx, 则h′(x)=ex-sinx-lnx-1. 设g(x)=h′(x),则 所以g(x)>g(1)=e-sin1-1>0. 即得h′(x)>0. 于是h(x)在(1,+∞)上单调递增. 所以h(x)>h(1)=e+cos1-1>0. 即ex+cosx-1-xlnx>0. 故xlnx 所以f(x+m) 综上,f(x+m) 例5 (2019年全国Ⅰ卷文20)已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数. (1)证明:f′(x)在区间(0,π)存在唯一零点; (2)若x∈[0,π]时,f(x)≥ax,求a的取值范围. 解析(1)设g(x)=f′(x),则 g(x)=cosx+xsinx-1, g′(x)=xcosx. 所以f′(x)在区间(0,π)存在唯一零点. (2)由题设知f(x)≥ax,f(π)=0,可得a≤0. 由(Ⅰ)知,f′(x)在(0,π)只有一个零点,设为x0,且当x∈(0,x0)时,f′(x)>0;当x∈(x0,π)时,f′(x)<0,所以f(x)在(0,x0)单调递增,在(x0,π)单调递减. 又f(0)=0,f(π)=0, 所以,当x∈[0,π]时,f(x)≥0. 又当a≤0,x∈[0,π]时,ax≤0,故f(x)≥ax. 因此,a的取值范围是(-∞,0]. 评注①对于零点不可求问题,常见的做法是“设而不求”.通过设出未知数作为桥梁进行消元或整体代换,这种数学思想在函数与导数问题中有着广泛应用.②要求证一个函数“有且只有一个”零点,可先用“函数零点的存在性定理”证明函数存在零点,再证明函数为单调函数,即得函数零点的唯一性.其依据为:如果函数f(x)在区间[a,b]上是单调函数,并且f(a)·f(b)<0,则函数f(x)在区间(a,b)上至多有一个零点.如果要证明函数有多个零点,一般要将分区间讨论解决,由于涉及三角函数,在判断导数的符号时,注意不同区间正弦、余弦函数值的正负[3]. 由上述例子可看出,导数与三角函数交汇的题型众多,融合函数、导数、不等式等重要知识点于一体,函数的表达式多是三角函数与ex,lnx相结合.问题方面主要与函数的单调性、零点、极值与最值、恒成立问题、证明函数不等式等主干内容相关,多个知识点综合在一起.由于三角函数的特殊性,所以不单考查导数公式和导数的运算法则,还可能考查三角函数中的恒等变换、周期性、有界性,常见的三角不等式等.综合度较高,对于考生运用所学知识,寻找合理的解题策略以及推理论证能力有较高的要求. 因此,在复习备考中要注重以下两点: ①突出主干知识.导数试题注重对导数的几何意义、导数的运算法则、导数在研究函数中的应用等重点内容的考查,函数单调性是核心性质,要深化对函数单调性的认识,复习时应注重导数法在函数单调性中的应用. ②注意总结,归纳提炼方法.复习时要善于总结,将涉及三角的函数导数试题分门别类,并归纳出常用的解法与注意事项,并通过题目的训练,举一反三,触类旁通.4 三角函数与对数型、指数型函数组合
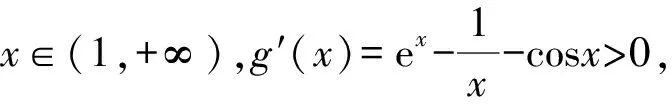

5 多个三角函数与其他函数组合
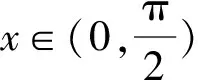

6 结束语

