具有年龄结构的异质元胞自动机HIV传播模型

王仲君，张莉丽

(武汉理工大学理学院，湖北武汉430070)

从1989年发现第一例本土艾滋病例至今，HIV感染已经覆盖全国，部分地区感染严重，在中国疫情的流行呈现出多样化特征，并从高危人群逐渐向一般人群扩散，虽然艾滋病的死亡率已有下降趋势，但艾滋病的防治形势仍然极其严峻［1－3］。若利用数学方法对艾滋病的传播过程进行模拟实验，找到影响艾滋病传播的相关参数，将对艾滋病的防治工作有重要意义。

目前流行病数学模型主要有微分方程、元胞自动机等，而基于元胞自动机的流行病研究在微观和宏观方面都得到了迅速的发展［4－7］，由于艾滋病是一种比较特殊的行为性流行病，传播过程与个体间行为有很大关联。目前艾滋病的模型研究多考虑在一些特定人群、特定传播路径下的演化过程。有一些学者提出个体“异质”性，考虑个体具有不同的抵抗力、感染能力等，也有对元胞空间进行扩展，考虑元胞的全局演化过程［8］。

基于上述分析，笔者考虑个体具有不同的年龄结构、不同的抵抗力和感染能力，依距离建立距离影响函数，并考虑个体间的致病性接触行为，建立适合的元胞自动机转换规则，在高危人群和一般人群中分别对HIV传播行为进行模拟研究，并与实际数据相比较，得到更具真实性的传播模型。

1 模型建立

笔者所提出的模型基于如下假设:①不考虑个体自然死亡与自然出生;②不考虑个体迁入或迁出;③迭代步长t为一个季度。

1.1 元胞状态

从感染HIV病毒到发病，有一个完整的自然过程，为简化模型便于研究，此处主要把人群分为4类:易感者、感染后未发病者(处于潜伏期)、感染且发病者、发病后死亡者。设潜伏期持续时间为t1，发病期持续时间为t2，t时刻元胞状态有以下4种情况:

几乎所有的HIV感染者经过一段潜伏期后都会进入典型艾滋病期，在没有医疗干预的情况下会很快死亡，HIV的发病期很短，一般为9个月左右，在未经治疗的情况下，平均潜伏期为7～10年，其中有部分感染者病情发展迅速，潜伏期可短至2～3年;还有部分感染者病情发展缓慢，潜伏期可延长到12年以上。

1.2 元胞的异质性

1.2.1 年龄变量

大量统计数据表明不同年龄群体感染HIV后发病率不一样，其中0～20岁个体发病率最低，50岁以上个体发病率最高，群体发病率与多种因素有关，此处考虑年龄及潜伏期长短对发病率的影响，设最初个体(i，j)的年龄变量为 age(i，j)，将人群年龄分为 5个阶段，A1=(0，19)、A2=［20，29］、A3=［30，39］、A4=［40，49］、A5=［50，+∞)，其中A1阶段内个体具有最长潜伏期时间，A5阶段内个体具有最短潜伏期时间，Ai阶段内个体具有潜伏期时间为t1i。

由于个体年龄每年都增加一岁，为便于模拟只考虑健康个体年龄的增加，而忽略已感染个体的年龄增加及个体自然死亡情况，此处假设所有个体的艾滋病发病时间为3个季度，即t2=3。

1.2.2 个体的传染强度及抵抗能力

设t时刻，携带HIV病毒的个体(i，j)对健康个体的传染强度为，研究表明艾滋病患者发病期的传染能力要远远大于潜伏期的传染能力，传染能力随时间也会不断增强，此处简单假设满足如下的关系:

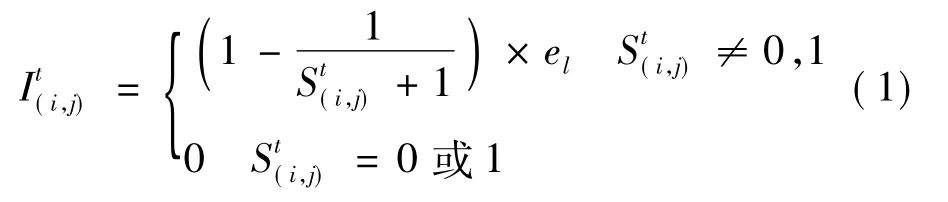
其中，el为控制传染强度的强度系数，结合真实数据及实验模拟确定。

设mt(i，j)为 t时刻，个体(i，j)的抵抗力，可理解为在一次接触中，个体不会受到感染的概率。由于个体行为差异性，其抵抗力各不相同［9］，这里假设mt(i，j)取值服从(0，1)的均匀分布。

1.3 邻域定义

设(i0，j0)为中心元胞在网格中的坐标，网格中的任一元胞(i，j)对中心元胞(i0，j0)的距离影响分值为 w(i，j)，则 w(i，j)满足如下关系［10－11］:

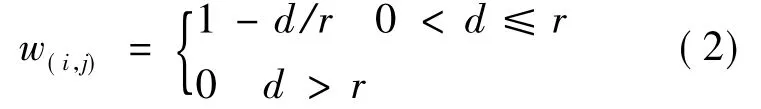
式中:d为元胞(i，j)到中心元胞(i0，j0)的几何距离，的影响半径。如果中心元胞(i0，j0)在元胞(i，j)的影响半径内，则(i，j)在(i0，j0)邻域内;如果中心元胞(i0，j0)不在元胞(i，j)的影响半径内，则(i，j)不在(i0，j0)邻域内。

1.4 邻域内元胞对中心元胞的影响力

艾滋病作为一种高致病性的行为性疾病，主要体现在性接触、血液感染等传播途径上，并且在不同的传播途径下，个体具有不同的感染率，其中血液传播的感染率达到95%。相反健康个体与艾滋病患者握手、拥抱、共餐、共用卫生间及游泳池等，都不会感染上HIV病毒。此处为简化模型，暂不单独考虑不同传播途径下的传播情况，引入函数来判断t时刻在一次接触行为下，元胞(i，j)与中心元胞(i0，j0)之间是否有致病性接触行为。函数定义如下:

若It(i，j)=0，元胞间无致病性接触行为，则 t时刻邻域内元胞(i，j)对中心元胞的影响力较小，影响力计算公式如下:

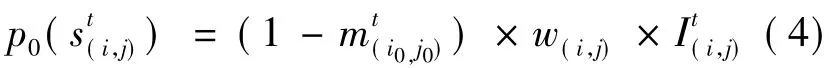
若It(i，j)=1，邻居元胞(i，j) 与中心元胞(i0，j0)有致病性接触行为，对中心元胞的影响力很大，结合在不同传播路径下，个体感染率情况，假设传染强度为0.95，此时忽略距离影响分值，影响力计算公式如下:

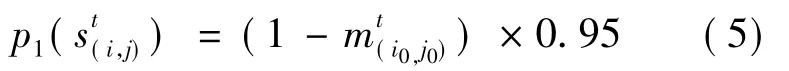
1.5 元胞状态更新规则

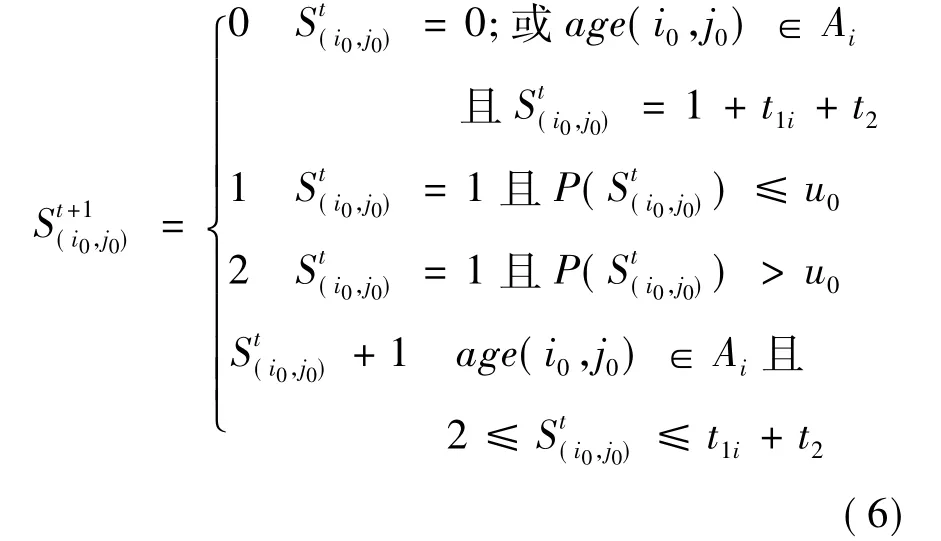
式中:age(i0，j0)为健康个体被感染时个体的年龄;P(St(i0，j0)) 为中心元胞(i0，j0) 在 t时刻被感染的概率，

2 仿真结果及分析

基于上述模型，假设初始感染者均处于潜伏期，群体年龄结构简化为两类，年轻个体潜伏期为36，年老个体潜伏期为8，结合C++语言，在不同初始人群感染率下，在100×100二维规则网格中进行模拟实验。

2.1 普通人群中HIV传播

据统计，我国艾滋病人群平均感染率为0.05%。假设初始人群感染率为0.05%，初始感染个体随机分布于网格中，一次迭代过程中个体间最多有一次致病性接触行为，分别模拟在不同元胞影响半径、不同初始人群数下HIV的传播。

图1为总感染人数变化图，其中图1(a)是初始人群数为8 000，元胞影响半径r分别为1、2、3、4的感染人数变化图;图1(b)为元胞影响半径r=3，初始人群数量分别为 4 000、5 000、6 000、7 000、8 000的总感染人数变化图。如图1所示，元胞影响半径越大，艾滋病传播速度越快，感染人数越多，较早达到峰值;元胞影响半径较小时无新增感染者，艾滋病不能传播开来，且感染人数呈现出阶梯型下降;同时初始人群数越大，HIV的传播速度越快，HIV感染人数越多。元胞的影响半径类似于个体的活动范围，如果可以控制感染个体的活动范围并对其隔离，就可以在一定程度上控制艾滋病的传播速度，然而当代便捷的交通扩大了个体的活动范围，也就增加了HIV传播行为的复杂性［12］。中国是一个人口大国，各地区的人群密度、人群分布、人群结构差异大，尤其是一些大城市，人口构成很复杂，艾滋病的传播行为随之变得复杂，而HIV正趋向于由特殊群体向一般人群扩散，艾滋病的防治预防工作显得尤为重要。

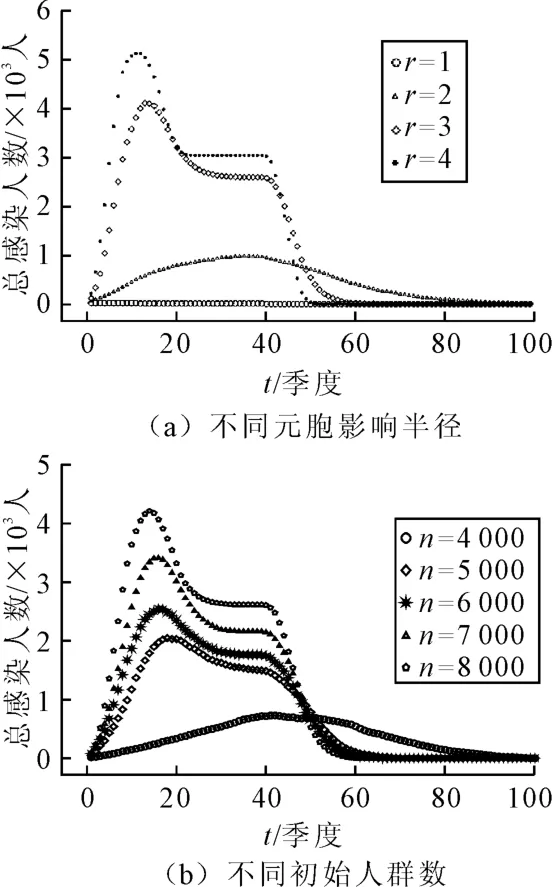
图1 总感染人数变化图

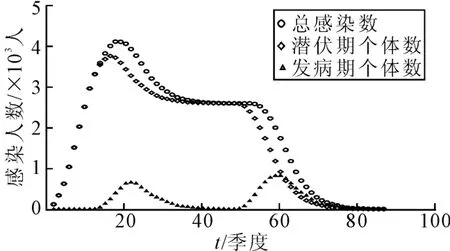
图2 相关感染人数变化统计图

图3 不同时刻的演化结果图

图2 是初始人群数为8 000，r=3时相关感染人数变化图;图3为对应的部分时刻演化结果，图中黑色元胞代表发病个体，深灰色元胞代表潜伏期个体，浅灰色元胞代表健康个体。对比发现开始时HIV感染者集中分布于病源附近，总感染人数迅速增加，在t小于8时，无艾滋病发病者;t大于8时，在病源附近的部分中老年感染个体首先发病，发病人数与潜伏期人数相比呈现出一定的滞后性增长和下降。演化步长为36前一段时间内，在网格空间限制下，潜伏期个体数不变，而发病个体数较低甚至为0。此时若个体不主动进行检测，由发病情况可大致判断艾滋病“消失”了，但随着时间的增长，病源附近部分未发病的年轻感染个体在经过漫长潜伏期后逐渐发病，发病人数激增，艾滋病再一次爆发。可见群体年龄结构影响艾滋病的爆发情况，短期的艾滋病“消失”现象不能忽视，仍然要做好防治工作。

2.2 艾滋病高发地区HIV传播

在性接触、血液接触等行为下艾滋病的感染率较大，在一些特殊群体中感染率最高达到5%，这里假设HIV初始感染率为2.5%，初始人群数为4 000，元胞影响半径r=3，考虑在一次迭代过程中，个体之间存在致病性接触行为数最多分别为1、2、3这3种情况，这里假设初始感染者分布在网格中心位置，便于观察传播现象。

(1)总感染人数比较。模拟过程中发现HIV由病源中心向四周扩散，致病性接触的次数越多，传染速度越快，感染面积越大，在较高致病性接触次数下，艾滋病很可能成为地方病。同时个体间不存在致病性接触行为时，即使初始感染率很高，在模拟过程中无新增感染者，初始感染个体经过潜伏期、发病期后死亡。如图4所示，在一次迭代过程中健康个体与感染个体之间的致病性接触次数越多，HIV感染率越大，艾滋病的传播速度越快，感染人数越多，群体的死亡率越高。在艾滋病高发地区，一定存在着与当地经济、社会相关的一条传播途径，要有效控制艾滋病的传播，首先要找到在该地区艾滋病传播的主要途径，再有针对性地对其进行行为教育控制，减少致病性接触行为次数，降低艾滋病的感染率及传播速度。

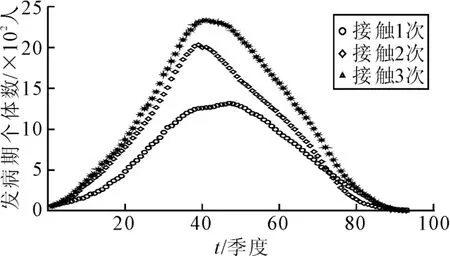
图4 总感染人数变化图

(2)发病人数比较。模拟过程中发现某些个体离病源距离虽近，但被感染后发病时间较迟，有些个体距离中心感染区较远，但是被感染后较早发病死亡，体现了个体年龄差异性对潜伏期及发病情况的影响，发病期个体数随时间变化的数据也说明了这一问题。图5为3种不同致病性接触次数下发病期个体数的变化图，这3种情况下，发病期个体数基本呈现出先增加后减少的趋势，但波动较大。在演化步数t小于8时，无艾滋病发病者，这是因为模型假设中老年个体的潜伏期为8，而年轻个体的潜伏期为36，所以t在16～36之间时发病个体都是老年个体，在演化步数大于36后，各年龄的感染个体都有可能会发病，整个群体的发病情况就变得复杂了。随着个体年龄增长，中老年个体数增加，其较短的潜伏期在一定程度上影响发病人数，而前期感染的年轻个体经过漫长的潜伏期后也会发病，发病个体数波动较大。若发病个体数下降则说明新增发病个体数小于新增死亡人数，这与潜伏期个体数及年龄结构有一定的关联。这3种模拟情况下发病人数最后都会大幅度下降，这可能是因为网格规模限制了潜伏期个体数，潜伏期个体数大量降低导致发病期的个体数相对也大量减少。可见在没有药物治疗的前提下，个体的年龄结构确实在一定程度上影响HIV传播。

2.3 实际数据比较分析

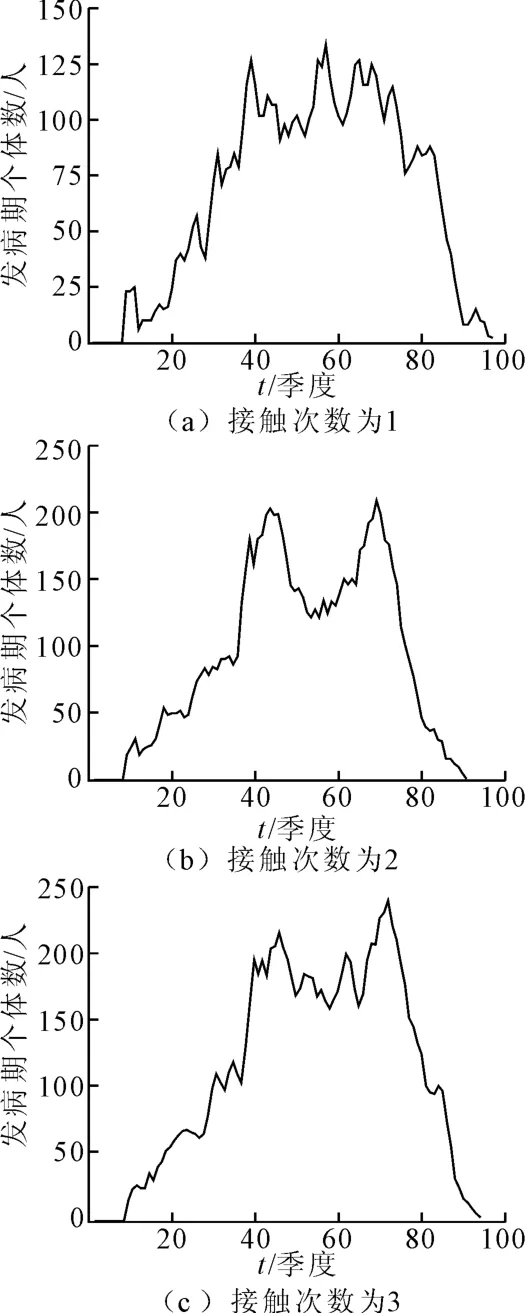
图5 发病人数变化图

图6 给出了武汉市2001—2011年的艾滋病感染人数变化情况，与本实验所模拟得到的发病人数变化图相比，具有一定的相似性，故考虑年龄属性来研究艾滋病的传播具有一定的真实性。

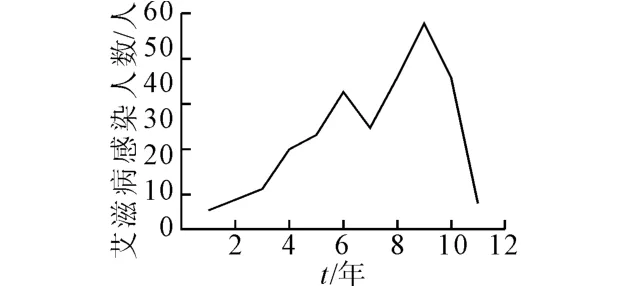
图6 艾滋病感染人数变化图

3 结论

元胞自动机模型曾多次用于流行病传播研究，笔者从年龄结构、传染能力等方面扩展元胞自动机模型，并考虑元胞间是否有致病性接触行为以及致病性接触行为的次数对HIV传播行为的影响，最后在两类人群下模拟实验，得到相关参数对HIV传播行为的影响。仿真结果发现初始人口数、元胞影响半径仍然影响HIV的传播速度及感染率，致病性接触行为对HIV传播速度影响较大，年龄结构在一定程度上影响群体的HIV感染分布，初始人群数、致病性接触次数、元胞影响半径及年龄结构相互作用，共同影响着HIV在群体中的传播，在某些取值条件下，群体总感染人数及发病期人数呈现出一些固定的变化规律，可进一步研究这些规律从而对艾滋病的预防控制提出科学合理的建议。

［1］LU L，JIA M，MA Y，et al.The change face of HIV in China［J］.Nature，2008，455(7213):609 －611.

［2］陶剑，陈朝银.艾滋病预防的现状与展望［J］.中国预防医学杂志，2010，11(5):534 －539.

［3］齐小秋.中国艾滋病防护联合评估报告［R］.北京:国务院防治艾滋病工作委员会，2007.

［4］ROUSSEAU G，GIORGINIB.Dynamical phases in a cellular automaton model for epidemic propagation［J］.Physica D，1997(103):554－563.

［5］MAYIL B V，PANDIARAJA D.Cauchy－eulermodel，cellular automata simulation of the rate of recovery of the infected airway from COPD［C］∥Informatics and Medical Engineering:Proceedings of the International Conference on Pattern Recognition.New Delhi:［s.n.］，2012:21 －23.

［6］张庭.基于异质元胞自动机的SARS传播［J］.系统工程理论方法应用，2006，15(3):205－210.

［7］段晓东，王存瑞，刘向东.元胞自动机理论研究及其仿真应用［M］.北京:科学出版社，2012:170－180.

［8］周金龙，王仲君.基于克隆选择的免疫算法研究［J］.武汉理工大学学报:信息与管理工程版，2012，34(6):726－728.

［9］李璐，宣慧玉，高宝俊.基于元胞自动机的异质个体HIV/AIDS传播模型［J］.系统管理学报，2008，17(6):704－710.

［10］钟少波，张毛磊.基于空间实体的传染病蔓延模拟建模研究［J］.计算机工程和应用，2008，44(18):190－193.

［11］FUENTESM A，KUPERMAN MN.Cellular automata and epidemiological models with spatial dependence［J］.Physica A，1999(267):471 －486.

［12］LIHW，JIANG Y S，APD E.Model of HIV transmission with social behavior［J］.Journal of Biomathematics，2009，24(4):620 －623.