基于Holt－W inter模型的建设用地需求量预测

孙 慧，盛 筠，陈扬杨

(天津大学管理与经济学部，天津300072)

建设用地需求量预测是根据区域建设用地的历史条件、区域发展规划及人们日益增长的生活需求，对一定时期内该区域的各项建设用地总规模的变化进行预测。建设用地需求量预测方法层出不穷，时间序列分析法、灰色预测分析法、马尔可夫预测法关注建设用地本身;而分类预测、回归预测，以及人工神经网络分析预测法等关注建设用地需求量与其影响因素之间的关系［1－2］;同时还有一些其他的预测方法，如双因素分析预测法、线性规划模型、蒙特卡洛仿真预测等［3］。数学模型和GIS方法是国外学者对于建设用地需求量预测的常用方法。美国林肯土地政策研究所采用GIS技术，根据土地的不同利用途径将土地划分为若干等级，预测土地容量，研究建设用地规模［4］。同时，CLARKE修正了元胞自动机模型(CA模型)，将旧金山海湾地区进行网格化处理，并对每个单元赋予相应土地利用类型的值，通过定义演化规则，调整规则参数，以实现对该区域土地需求量的预测［5］;国内方面，苏雷［6］、朱小利［7］、袁健等［8］、邱道持［9］针对建设用地需求量的影响因素，运用ARMA模型、回归分析、灰色系统、双因素分析等方法，建立需求量与影响因素的逻辑关系模型，间接得出未来一段时期城市建设用地需求量。曹立伟采用新古典经济学与发展经济学相结合的一般均衡模型方法建立了城镇建设用地的一般均衡模型，运用通用数学建模系统得出了2010年和2020年的南宁市城镇建设用地需求量［10］。

从国内外研究现状来看，现有研究存在着建设用地预测模型使用条件严格、可操作性差、适用性不强，以及对于建设用地需求量的影响因素研究不够等问题。因此，需要在考虑其他因素对建设用地需求量影响的基础上，采用较为简洁的预测方法，建立建设用地与影响因素之间的关系模型，同时还应考虑模型的适用范围、预测精度，使预测结果更为精确。基于此，笔者采用多元线性回归建立模型，运用Holt－Winter对各影响因子长期变化量进行预测，从而得到较远阶段的建设用地需求量。

1 预测模型的构建

1.1 影响因素选取

影响建设用地变化的因素很多，涵盖经济、社会、环境、政策等诸多方面［11］，因素相互关系非常复杂，因此，笔者从某市建设用地现状出发，分析各影响因素与建设用地的关系，寻找对建设用地变化影响较大的关键成功因素，建立这些关键成功因素与建设用地之间的关系模型，为建设用地需求量的预测打基础。为此，笔者对用来筛选建设用地需求量影响因素的181篇文献进行了分析与统计，其影响指标如表1所示。

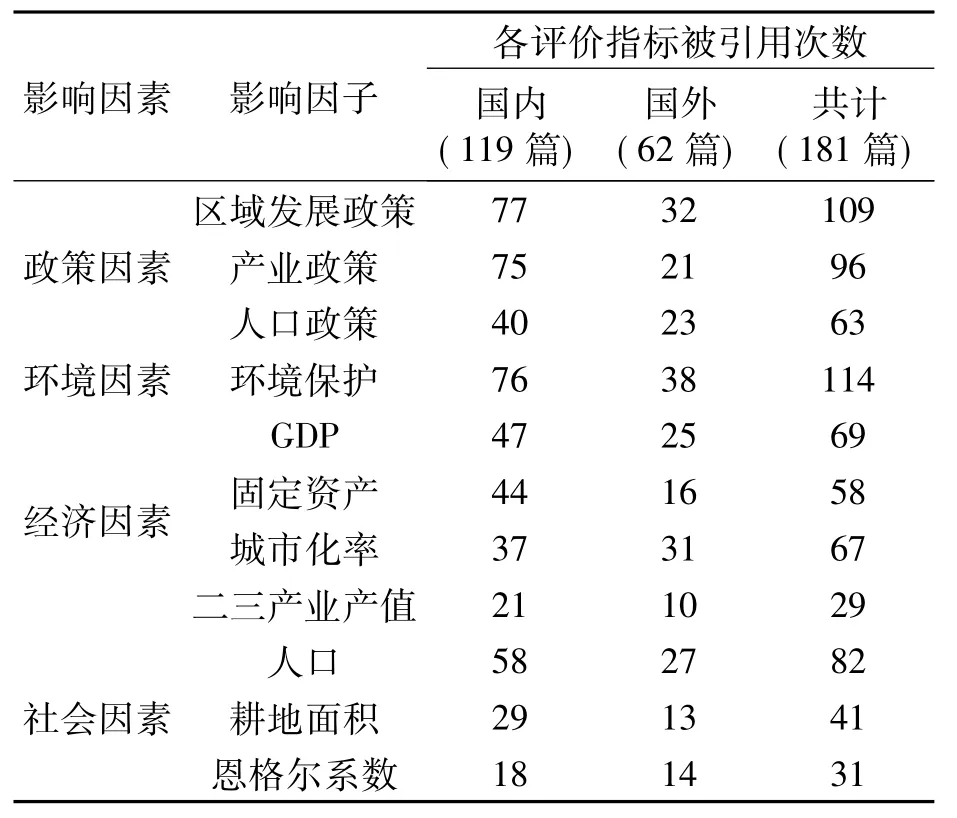
表1 建设用地变化影响指标

建设用地需求量的影响因素涉及面比较广，其中环境、政策方面的影响因素多为定性指标，难以量化，因此笔者采用经济、社会两方面的影响因素来进行研究，对于这两类影响因素不同学者侧重于不同的因子，如表2所示。

表2 国内外学者对建设用地需求量影响因素的研究

从表2可以看出，国内外学者从多方面对建设用地需求量影响因素进行了研究分析，其中关注最多的影响因素为国内生产总值、固定资产投资、常住城市化水平和人口。其中国内生产总值(GDP)、固定资产投资和城市化水平是经济方面的影响因素。国内生产总值的变化会影响社会经济的发展，同时二、三产业的发展又需要借助建设用地规模来实现;固定资产投资的变化，导致土地利用方向和土地利用结构发生变化，也间接地影响到建设用地规模;城市化率在一定程度上反映了预测区域的城镇化水平，城镇化的推进带来了建设用地的扩张;人口为社会方面的影响因素，预测区域常住人口总数的增加，会带来各种非农业建设用地如居住用地、交通用地、基础设施用地量的相应增加。

1.2 多元线性回归模型

模型的选择主要考虑了两个原因，一是该模型考虑了建设用地变化的影响因素，可用两个或两个以上的影响因素作为自变量来解释因变量，即建设用地需求量的变化;二是在长期预测中，采用多元线性回归预测模型较为精确。多元线性回归模型研究的是因变量(被解释变量)与两个或两个以上自变量(解释变量)之间的回归问题。

(2)预测与置信区间。由回归方程^y=b0+b^1x1+b^2x2+…+b^pxp给定自变量的值，可以得出因变量的值。在给定置信度1－α的情况下，因变量单个值 Y0的置信区间为，其中

(3)统计检验。通过样本数据建立回归方程后，通常还需进行拟合优度、回归方程的显著性、回归系数的显著性等各种统计检验，以证明方程建立的有效性［17］，之后才能用于实际问题的分析与预测。常用的检验方法有:①拟合优度检验。多元线性回归模型采用样本决定系数R2(又称复决定系数)来进行拟合优度检验。②回归方程的显著性检验。采用F统计量对多元线性回归方程的显著性进行检验。

1.3 Holt－W inter模型预测相关影响因子

为客观预测未来建设用地需求量，仍需分别对模型中相关影响因素进行预测。笔者主要运用Holt－Winter对各个影响因子进行预测。Holt－Winter模型为指数平滑方法的一种，包括无季节模型、基于加法的季节模型和基于乘法的季节模型3种。

2 某市建设用地量预测

2.1 建设用地需求量影响因素相关性分析

根据上述建设用地影响因素，选取某市的国内生产总值X1、固定资产投资X2、常住人口X3和城市化率X4作为建设用地需求量的影响因子，以建设用地需求量作为输出因子，影响因素作为输入因子，在0.01的显著性水平下得到影响因素与建设用地需求量的相关系数如表3所示。

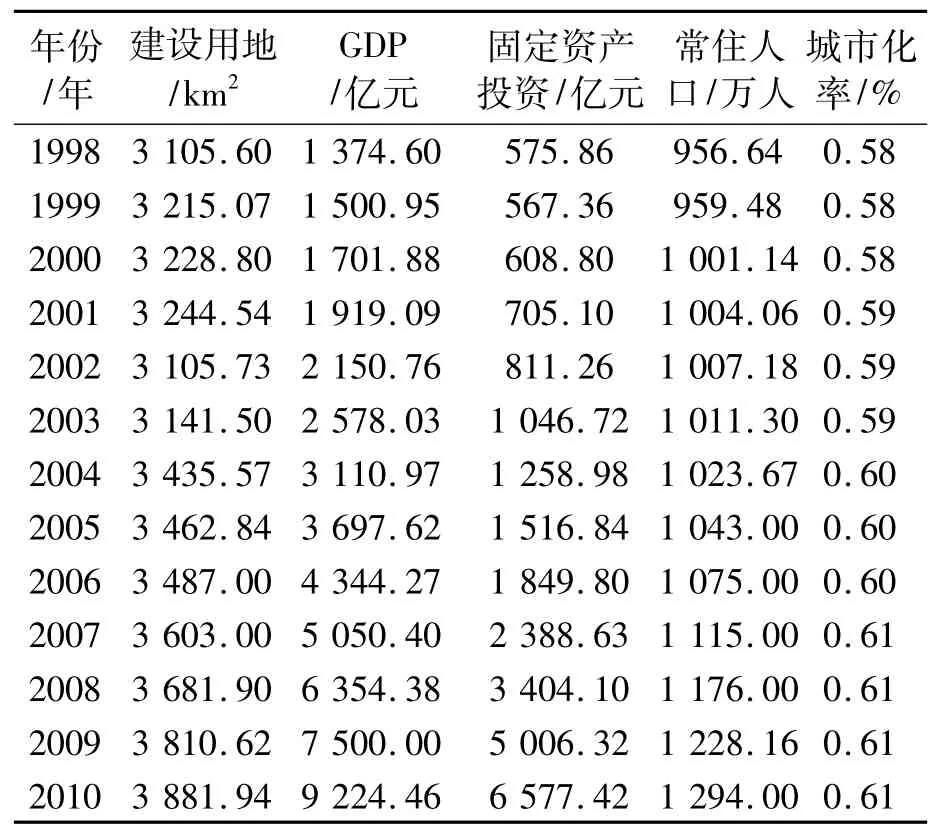
表3 某市建设用地及其影响因素数据

多元回归得 X1、X2、X3、X4的 Pearson 简单相关系数为0.958、0.916、0.944 和0.905，由此可知各影响因素与建设用地的相关系数都比较大，表示因变量与自变量之间的线性关系都非常显著。同时各个影响因素与建设用地间的相关系数为正，表明经济因素中各影响因子与建设用地之间都呈正相关关系。

2.2 构建多元回归模型及检验

通过SPSS软件进行多元线性回归，得到的多元回归系数如表 4 所示，自变量 X1、X2、X3、、X4的方差膨胀因子VIF均大于10，变量间的相关系数较高，故变量间存在严重的线性相关关系。因此需要用岭回归进行进一步修正，以消除共线性带来的影响。

2.3 多元线性回归模型的修正

由于影响因素之间存在共线性，因此运用岭回归进行进一步回归，得到岭回归系数，如表5所示，B为模型未标准化的系数，SE(B)为未标准化的系数标准误差，Beta为标准化系数，得到预测模型方程为 Y=0.03X1+0.03X2+0.52X3+6 972.28X4－1 457.7，同时得到 s(y)=27.49。

2.4 预测模型的检验

(1)拟合优度检验结果如表6所示，其中相关系数 R=0.966，R2=0.933，经调整后的 R2=0.900，估计标准误差为84.500。说明建设用地与常住人口、固定资产投资额、国内生产总值以及城市化率之间存在较为显著的线性相关关系。

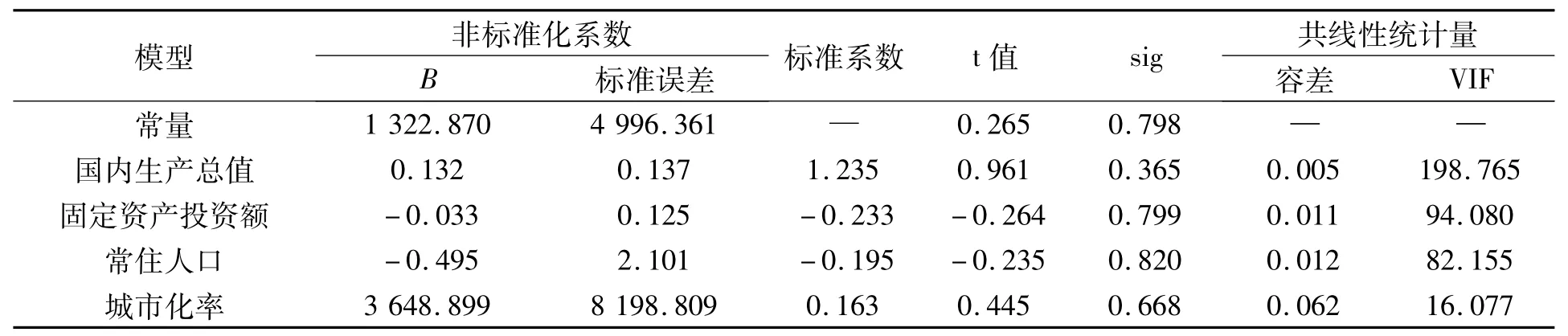
表4 多元回归系数

表5 岭回归系数

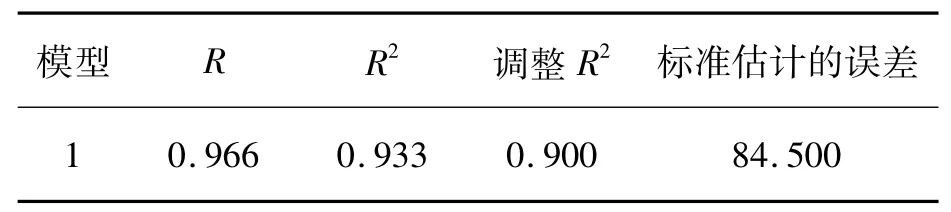
表6 拟合优度检验结果

(2)回归方程的显著性检验结果如表7所示，其中，F=28.07，F 分布的显著性概率为0.000，即检验假设“H0:回归系数 B=0”成立的概率为0.000，从而应该拒绝H0，说明回归效果极为显著。

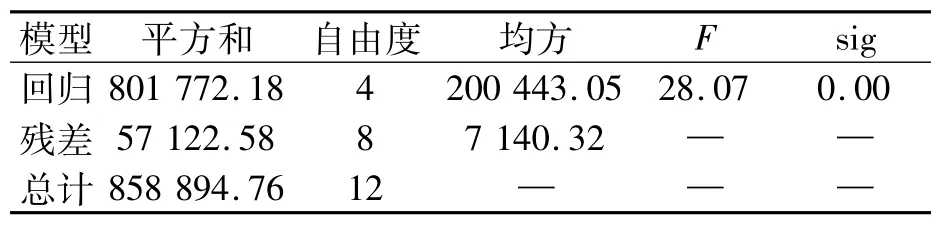
表7 回归方程显著性检验结果

2.5 相关影响因子的Holt－W inter模型预测

预测研究仅针对某市2011—2015年的建设用地需求量，属于短期预测，可以采取Holt－Winter预测模型对其影响因子(GDP、固定资产投资额、常住人口、城市化率)进行预测。首先，对国内生产总值(GDP)进行预测。某市1993—2010年国内生产总值情况如表8所示。

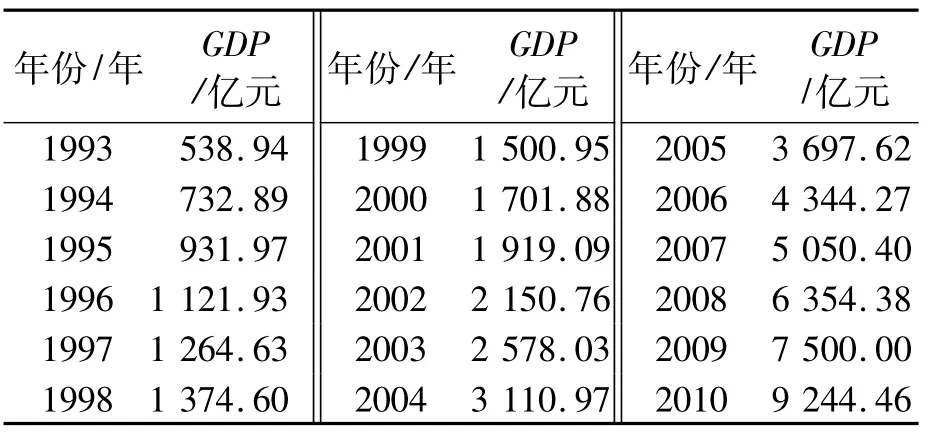
表8 某市国内生产总值

运用Eviews统计软件，分别将Holt－Winter预测的3种模型与国内生产总值的实际值进行拟合，结果显示采用无季节模型拟合的效果比较好。因此预测2011—2015年某市国内生产总值分别为10 845.23 亿元、12 518.03 亿元、14 190.84 亿元、15 863.65 亿元、17 536.45 亿元。其拟合曲线如图1所示。

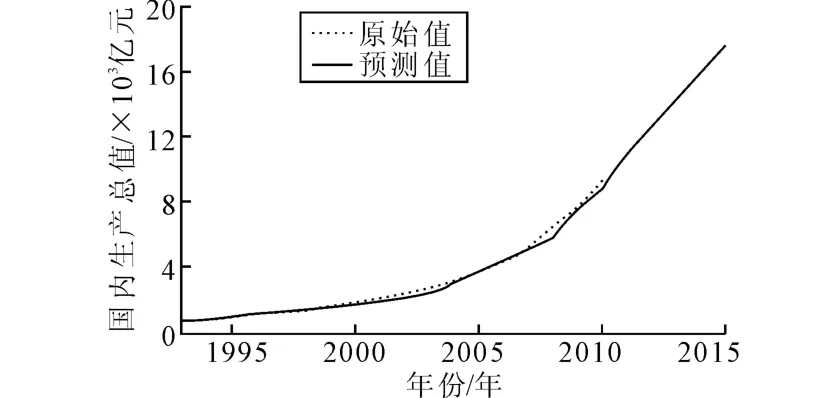
图1 国内生产总值预测图

与上述预测类似，对2011—2015年某市固定资产投资额、常住人口、城市化率分别进行预测，得到如下结果:2011—2015年某市固定资产投资额分别为 8 148.52亿元、9 719.62亿元、11 290.72亿元、12 861.82 亿元和 14 432.92 亿元;2011—2015某市常住人口分别为1 356.21万人、1 419.93 万人、1 483.65 万人、1 547.38万人和1 611.10万人;2011—2015年某市城市化率分别为61.43%、61.70%、61.97%、62.24%和62.51%。

结合上述预测方程 Y=0.03X1+0.03X2+0.52X3+6 972.28X4－1 457.7，可得 2011—2015年建设用地需求量分别为 4 100.413 km2、4 249.690 km2、4 398.967 km2、4 548.249 km2和4 697.525 km2。由以上分析得出 s(y)=27.49，因此某市2011—2015年建设用地需求量预测值如表9所示。

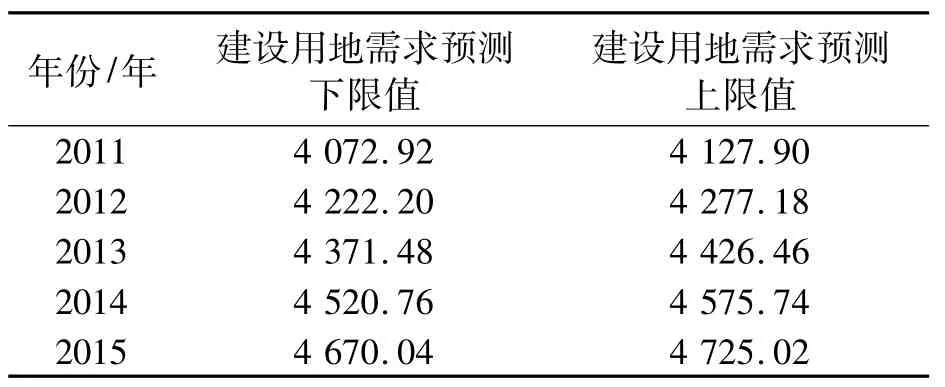
表9 某市2011—2015年建设用地需求预测值km2

3 结论

笔者对土地利用总体规划中建设用地需求量的预测方法进行了归纳与总结。考虑到社会、经济、政策、环境等多方面因素都不同程度地影响建设用地需求量的变化，故采用多元线性回归模型，建立建设用地与主要影响因素之间的关系模型，通过对各因素的预测来间接预测未来5年建设用地的需求量。由于4个影响因素之间存在较为明显的共线性，因此又采用了岭回归对以上线性模型进行修正。对于多元线性回归中自变量，即影响因素的预测，又引入Holt－Winter无季节、加法、乘法模型，并分别将其运用到建设用地影响因素的预测中，经过对比，选择预测值与实际值拟合程度较高的模型来进行预测，最终得出某市2011—2015年建设用地需求量。

［1］姜海，曲福田.建设用地需求预测的理论与方法:以江苏省为例［J］.中国土地科学，2005，19(2):44－51.

［2］刘金国，张希.中国城市建设用地需求量预测研究综述［J］.国土与自然资源研究，2011(2):16－18.

［3］陈百明，张凤荣.我国土地利用研究的发展态势与重点领域［J］.地理研究，2011，30(1):1 －8.

［4］THOMASSN，SKITMOREM，WONG K F.Using genetic algorithms and linear regression analysis for private housing demand forecast［J］.Building and Environment，2008，43(6):1171 －1184.

［5］CLARKE K C.A self－ modifying cellular automaton model of historical urbanization in the San Francisco Bay area［J］.Environment and Planning，1997(24):247－261.

［6］苏雷.ARMA模型在土地利用需求量预测中的应用［J］.湖南农业科学，2012(5):61 －63.

［7］朱小利.土地利用规划中耕地需求量预测方法探讨［J］.西南农业大学学报:社会科学版，2010，8(2):5－10.

［8］袁健，李政，曾令文.建设用地需求预测与供地政策研究［J］.中国土地，2004(1):71－73.

［9］邱道持.城镇建设用地预测方法新探［J］.西南师范大学学报:自然科学版，2004，29(1):146－150.

［10］曹立伟.基于可计算一般均衡模型的城镇建设用地需求预测研究［D］.桂林:广西师范大学图书馆，2012.

［11］王科星.昆明市建设用地需求量变化影响因素分析［J］.资源环境与节能减灾，2012(2):154－157.

［12］唐华东.国家级开发区土地集约利用研究［J］.港口经济，2006(3):23－25.

［13］贺美利，周勇.预测分析武汉市在未来两个五年规划期内的住宅用地需求［J］.资源环境与工程，2008，22(2):257 －259.

［14］孙善龙，东野光亮，刘喜光.城乡建设用地需求量预测研究［J］.陕西农业科学，2008(5):169－172.

［15］刘胜华，詹长根.基于国民经济和人口发展目标的建设用地需求规模预测研究［J］.中国人口资源与环境，2005，15(5):47 －50.

［16］林建平，赵晓敏.城镇建设用地规模影响因素分析及预测［J］.国土资源科技管理，2008，25(2):102 －106.

［17］何晓群，刘文卿.应用回归分析［M］.北京:中国人民大学出版社，2011:76－132.