基于群组层次分析法的管制员绩效考核
杨新湦,张齐乐
(中国民航大学空中交通管理学院,天津300300)
1 管制员绩效考核中存在的问题
1.1 缺乏统一可行、科学合理的标准规范
当前大多单位存在着两套评价体系,即官方体系和同行之间的评价体系。不可否认,这两套评价体系各有其合理性和缺陷,但无论哪一种都因为在评价中参杂大量主观因素而导致评价结果偶尔会有失公允[1]。
1.2 指标的选取偏理想化
目前使用的绩效考核办法在指标的选取上存在两种极端:一是指标的选取过简,简单的指标体系减轻了测量指标数据的工作量,但并不能全面考察管制员的综合绩效,结果容易出现偏差;二是指标的选取过于繁琐,导致绩效考核工作与管制实际工作脱节,加大了收集指标数据的难度,缺乏可操作性。
1.3 涉及主客观的指标权重难以确定
主观赋权评估法采取定性的方法,由专家根据经验进行主观判断得到权重,再对指标进行综合评估。而实际中存在模棱两可、含糊不清的评判信息,对主观赋权法影响较大。客观赋权评估法则根据历史数据研究指标之间的相关关系或指标与评估结果的关系来进行评估,期望完全避免人为因素,而过高的量化标准会使绩效考核单纯地追求数量而忽视质量。
1.4 考核偏重于对结果的运用
考核是一种手段,而不是目的。不能仅依据考核结果就对管制员妄下定论,而应把考核结果作为更好地了解管制员的手段。创造一个公开、通畅的双向沟通环境,使考核者与被考核者能就考核结果进行及时有效的交流,并在此基础上制定管制员未来事业发展规划。
2 管制员绩效考核指标体系的建立
在建立管制员绩效考核指标体系时,充分考虑了我国空中交通管制发展现状,并吸取了国际上空中交通管制发展的宝贵经验。因此研究的管制员绩效考核指标体系是基于联邦航空局(FAA)在选聘管制员时的4项要求:Motivated(对待工作的积极性)、Decisive(处理工作时的决断力)、Committed(对待工作的忠诚度)、Self-Confident(自信度)。将这4项要求作为管制员绩效考核指标体系的一级指标。在选择二级、三级、四级指标时,参考了欧洲航行安全组织(EUROCONTROL)对管制员绩效考核的要求[2];同时参考了对管制单位管理层及一线管制员所做的大量问卷调查,并结合了心理学的有关理论。
3 确定管制员绩效考核指标权重
3.1 指标权重的设定
指标权重的设定是影响绩效考核结果最为重要的因素。传统确定绩效考核权重的方法多为模糊综合评价和层次分析法。模糊综合评价中隶属度数的确定还没有系统的方法。层次分析法首先结合专家意见,通过设立判断矩阵,检验一致性,计算指标权重,但实际中存在模棱两可、含糊不清的评判信息,影响了计算指标权重的结果[3-5]。
综合以上多种绩效考核确定权重的方法,笔者通过引入三角模糊数的群组层次分析法对传统的层次分析法(AHP)进行改进,将其拓展为群组模糊层次分析法(GFAPH)。这种方法能减少主观因素对权重计算的影响,相对传统层次分析法更具有鲁棒性,提高绩效考核结果的准确性和针对性[6-8]。
向10位管制领域专家发放问卷对各级指标进行两两比较打分,即构造判断矩阵,引用数字1~9及其倒数作为标度,如表1所示。
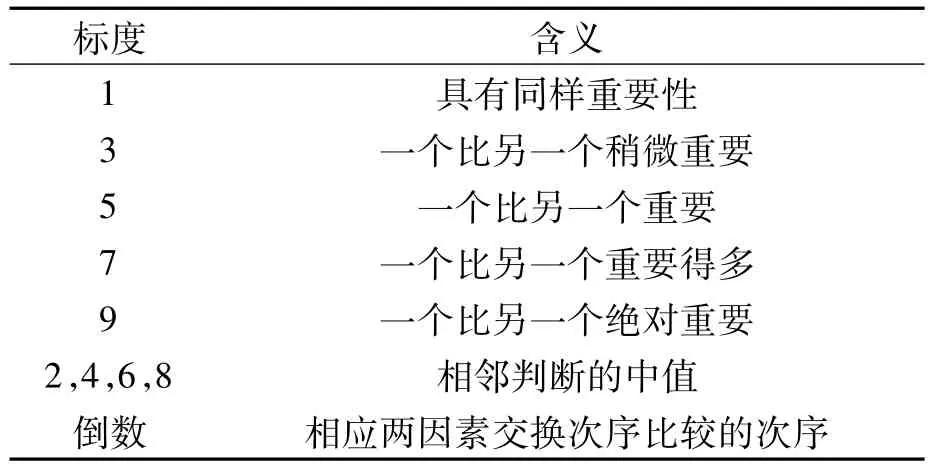
表1 判断矩阵标度及含义(两个因素比较)
3.2 确定一级指标权重
(1)收集10位管制领域专家对一级指标的打分记录,构造一级指标判断矩阵,现以第一位打分专家打分所得判断矩阵为例,如表2所示。以M表示对待工作的积极性,D表示处理工作时的决断力,C表示对待工作的忠诚度,S表示自信度。
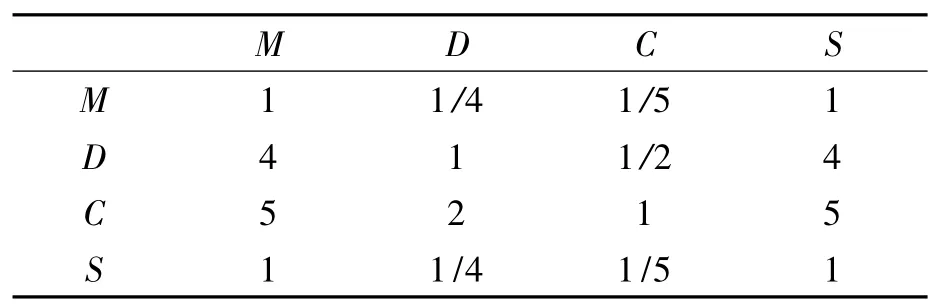
表2 一级指标两两比较专家打分记录
(2)检验判断矩阵A1的一致性。利用Matlab 7.0 计算出A1的最大特征值λA1max=4.027 7,查表得4阶矩阵的平均随机一致性指标RI=0.89,利用公式:
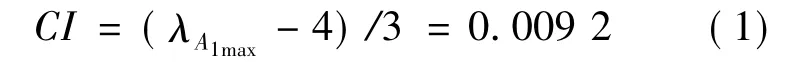
计算得 CR=CI/CR=0.010 <0.1,通过一致性检验。
(3)建立三角模糊评价矩阵。利用α-截集将判断矩阵A1分为最大矩阵A1max和最小矩阵
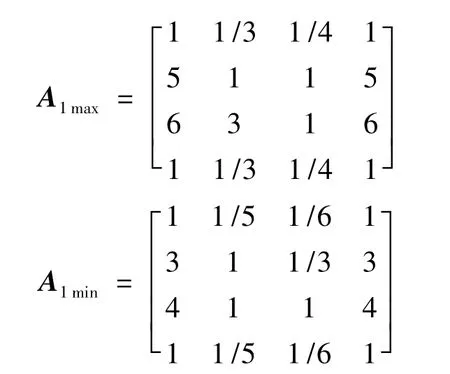
(4)计算模糊权重。设矩阵A1对应的权数(即最大特征值对应的特征向量)为Wb1,矩阵A1max对应的权数为Wc1,A1min对应的权数为Wa1。利用Matlab7.0计算可得:

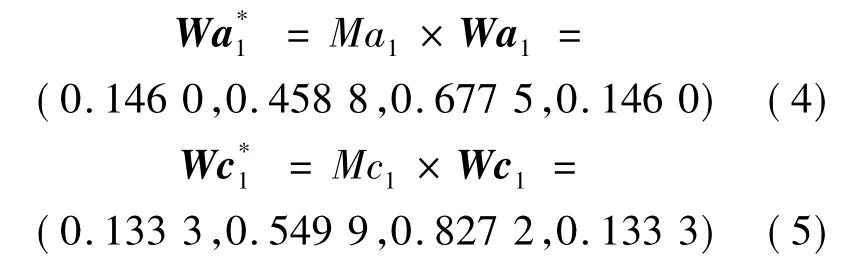
因此得到第一个管制专家的模糊权重矩阵:
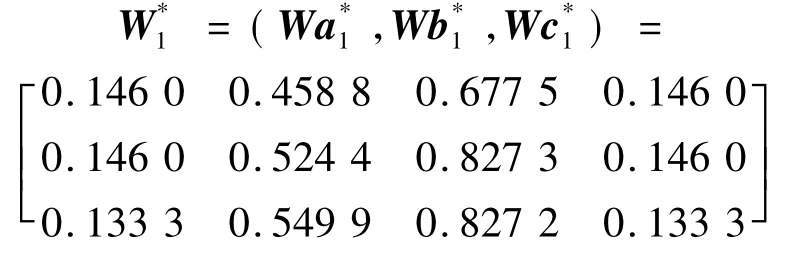
(5)求出另外9位专家的模糊权重矩阵。
首先判断是否通过一致性检验。
A2判断矩阵中,最大特征值λ=4.081 3,CI=(λ- 4)/3=0.027 1,CR=CI/RI=0.027 1 <0.1,满足一致性要求。
A3判断矩阵中,最大特征值λ=4.021 1,CI=(λ- 4)/3=0.007 0,CR=CI/RI=0.007 9 <0.1,满足一致性要求。
A4判断矩阵中,最大特征值 λA4max=4.000,CI=(λA4max-4)/3=0,CR=CI/RI=0 <0.1,满足一致性要求。
A5判断矩阵中,最大特征值λA5max=4.047 3,CI=(λA5max- 4)/3=0.015 8,CR=CI/RI=0.017 7 <0.1,满足一致性要求。
A6判断矩阵中,最大特征值 λA6max=4.071,CI=(λA6max- 4)/3=0.023 7,CR=CI/RI=0.026 6 <0.1,满足一致性要求。
A7判断矩阵中,最大特征值 λA7max=4.535,CI=(λA7max- 4)/3=0.178 3,CR=CI/RI=0.200 4>0.1,不满足一致性要求,因此去掉第7位专家的打分结果。
A8判断矩阵中,最大特征值 λA8max=4.074,CI=(λA8max- 4)/3=0.024 7,CR=CI/RI=0.027 8 <0.1,满足一致性要求。
A9判断矩阵中,最大特征值 λA9max=4.633,CI=(λA9max-4)/3=0.211,CR=CI/RI=0.237 1>0.1,不满足一致性要求,因此去掉第9位专家的打分结果。
A10判断矩阵中,最大特征值 λA10max=4.107 6,CI=(λA10max- 4)/3=0.035 9,CR=CI/RI=0.040 3 <0.1,满足一致性要求。
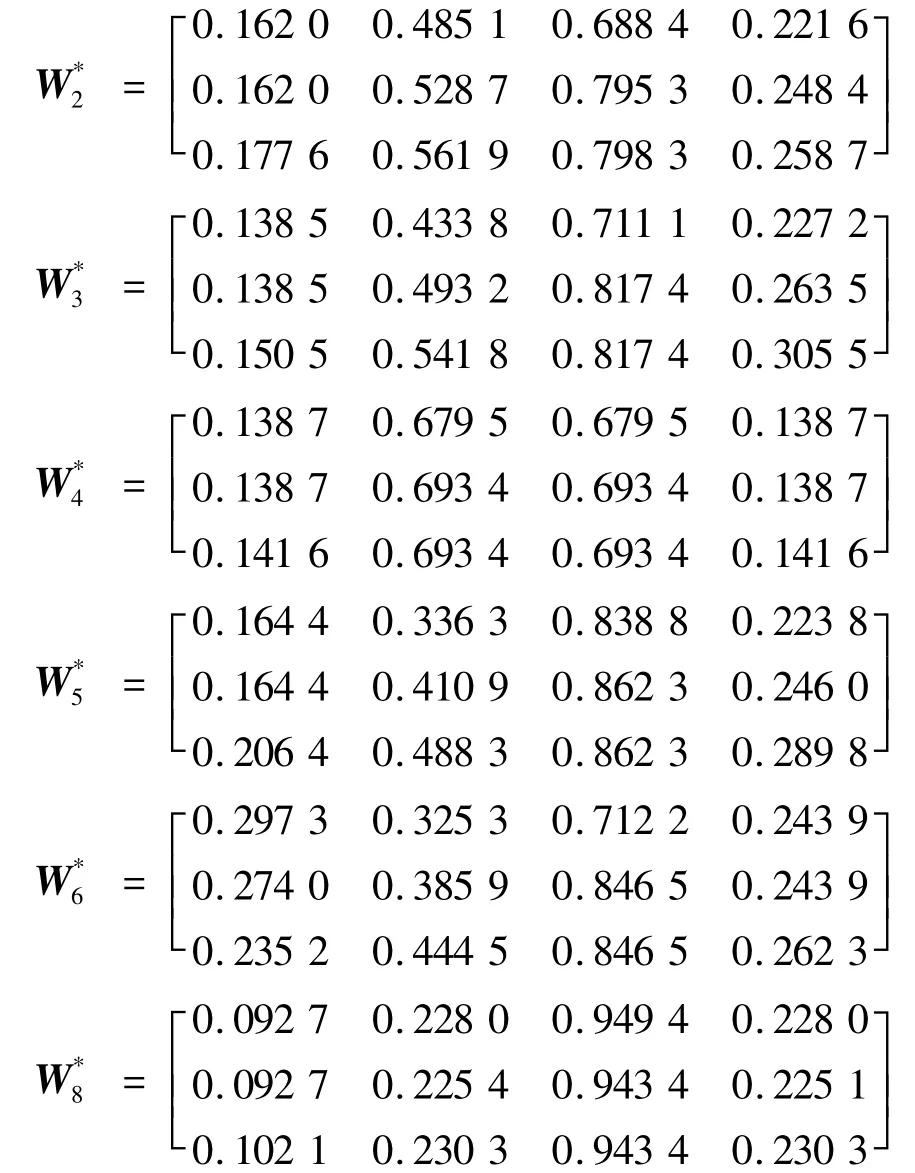
利用与上述相同的方法,求得已满足一致性检验的7位专家的模糊权重矩阵:

(6)计算通过一致性检验的8位管制专家关于一级指标的最终权重。
首先几何平均以上8位管制专家的模糊权重矩阵:
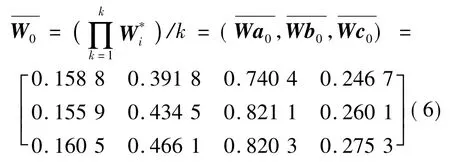
其中,k=8;i=1,2,3,4(列数)。
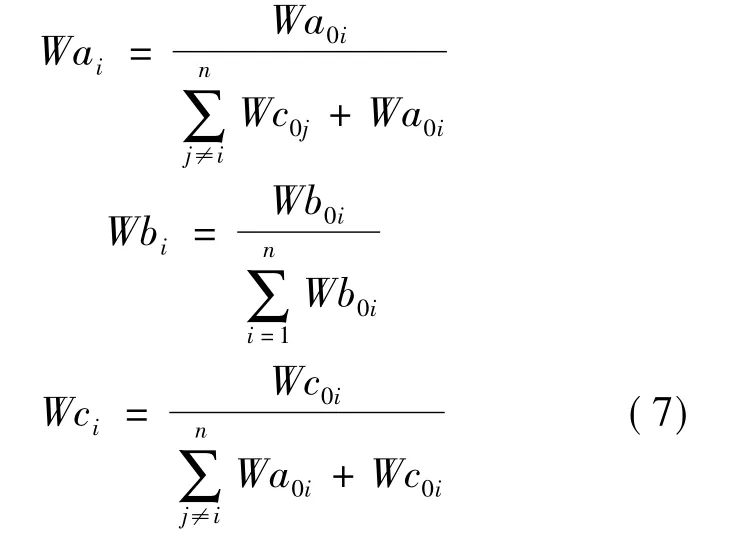

可得:在对每一列取几何平均并归一化,得到8位管制专家关于一级指标的最终权重:
W=(0.096 8,0.262 8,0.483 9,0.156 5)
3.3 确定二级、三级、四级指标权重
确定二级及以下指标权重的方法与确定一级指标权重的方法相同,其中需要注意的是只包含一个下级指标的其权重系数不必再计算,且两个指标进行判断时自然会满足一致性要求,只需验证有3个及超过3个指标的判断矩阵的一致性[9-10]。最后排除不通过一致性检验的专家打分。
(1)二级指标权重确定。
Motivated下设4个二级指标权重确定:
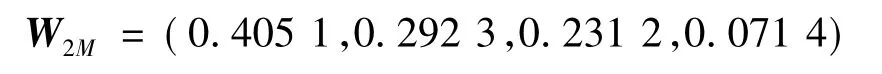
Decisive下设2个二级指标权重确定:
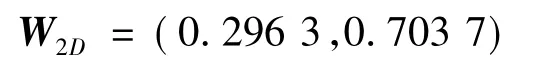
Committed下设6个二级指标权重确定:

Self-Confident下设5个二级指标权重确定:

(2)三级指标权重确定。
二级指标专业英语下设两个三级指标权重确定:
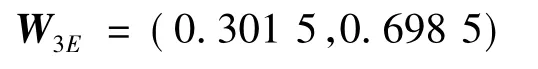
二级指标协调能力下设两个三级指标权重确定:
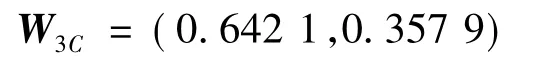
二级指标个人惩罚下设两个三级指标权重确定:
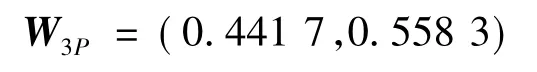
(3)四级指标权重确定。
三级指标团队协调能力下设两个四级指标权重确定:
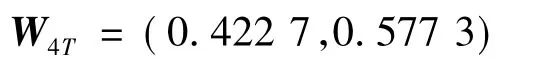
三级指标对外协调能力下设两个四级指标权重确定:
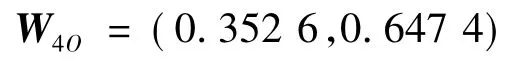
3.4 计算各级指标对总目标的组合权重
利用式(8)来计算各级指标对总目标的组合权重。
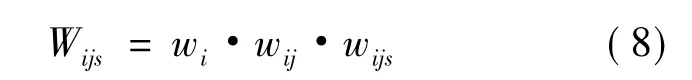
其中Wijs为各级指标对总目标的组合权重;wi为二级指标权重;wij为二级指标i下的三级指标权重;wijs为三级指标ij下的四级指标权重。权重计算结果如表3所示。
根据该管制员绩效考核体系,在北京、天津、西安各选取了10名管制员进行绩效考核分析,设置考核周期为一个月,考核结果在领导层、同事层以及被考核管制员心中认可度高,并着手计划周期为一年的考核工作。
4 结论
管制员绩效考核是及时了解管制员日常工作、甄别工作中遇到的问题、鉴定管制单位的水平及效益的有效手段,是加速空管单位发展的有力保障。参考FAA和EUROCONTROL对管制员工作的宝贵经验,并结合我国一线管制工作特点和对心理学个人效能的理解,建立了管制员绩效考核指标体系的一级指标。该指标克服了原有指标体系过于抽象、难以量化、难以测量的缺陷,更具有针对性。在算法的选择上,对传统的层次分析法进行改进,扩展为群组层次分析法,以求弱化个人主观影响,并引入三角模糊数进一步克服实际评判中存在模棱两可、含糊不清信息的影响。通过改进后的算法确定了管制员绩效考核指标体系的各项指标权重,并通过在一线单位的应用证明了算法的可行性。

表3 管制员绩效考核指标体系及对应权重
[1]项恒.空中交通管制员心理选拔指标的模糊综合评价[J].航天医学与医学工程,2009,12(6):422 -426.
[2]EUROCONTROL(2002).Survey-selection and recruitment of controllers[R].Luxembourg:EUROCONTROL Doc,2002.model of historical urbanization in the San Francisco Bay area[J].Environment and Planning,1997(24):247-261.
[6]苏雷.ARMA模型在土地利用需求量预测中的应用[J].湖南农业科学,2012(5):61 -63.
[7]朱小利.土地利用规划中耕地需求量预测方法探讨[J].西南农业大学学报:社会科学版,2010,8(2):5-10.
[8]袁健,李政,曾令文.建设用地需求预测与供地政策研究[J].中国土地,2004(1):71-73.
[9]邱道持.城镇建设用地预测方法新探[J].西南师范大学学报:自然科学版,2004,29(1):146-150.
[10]曹立伟.基于可计算一般均衡模型的城镇建设用地需求预测研究[D].桂林:广西师范大学图书馆,2012.
[11]王科星.昆明市建设用地需求量变化影响因素分析[J].资源环境与节能减灾,2012(2):154-157.
[12]唐华东.国家级开发区土地集约利用研究[J].港口经济,2006(3):23-25.
[13]贺美利,周勇.预测分析武汉市在未来两个五年规划期内的住宅用地需求[J].资源环境与工程,2008,22(2):257 -259.
[14]孙善龙,东野光亮,刘喜光.城乡建设用地需求量预测研究[J].陕西农业科学,2008(5):169-172.
[15]刘胜华,詹长根.基于国民经济和人口发展目标的建设用地需求规模预测研究[J].中国人口资源与环境,2005,15(5):47 -50.
[16]林建平,赵晓敏.城镇建设用地规模影响因素分析及预测[J].国土资源科技管理,2008,25(2):102 -106.
[17]何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2011:76-132.

