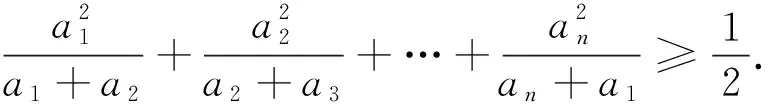配之以对偶 赋之以精魂
浙江省嘉善第二高级中学 (邮编:314100)
在数学里,在某种意义下成对出现的两个数学结构,如对偶点、对偶数、对偶式、对偶图、对偶空间、对偶运算、对偶命题,称之为对偶关系.若对于一个孤立的研究对象,有意识地构造与之相应的对偶关系,往往可获得新颖别致的解法.我们把这种解决问题的技巧称为配以对偶的技巧.运用该技巧的通常做法是:①将已知式令为,A并配其对偶式B; ②对A与B进行适当地运算;③转化或消去B,从而解决原问题.对偶式的形式往往不拘一格.主要有①互余型对偶式;②和差型对偶式;③对称型对偶式.
1 互余型对偶式
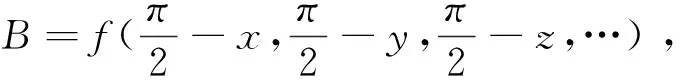
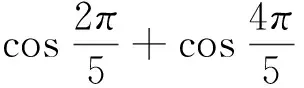

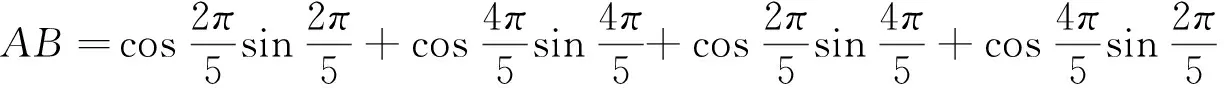
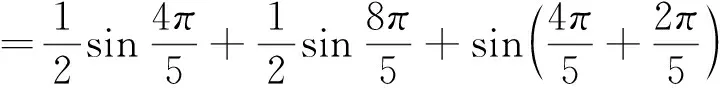
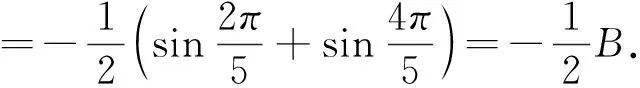
又b≠0, 故
例2 求sin280°+cos250°-sin40°cos10°
解由诱导公式可得
sin280°+cos250°-sin40°cos10°=cos210°+cos250°-sin40°sin80°,
构造对偶式:
x=cos210°+cos250°-sin40°sin80°
①
y=sin210°+sin250°-cos40°cos80°
②
由①+②得:x+y=2-cos40°
③
④
故
另解:构造对偶式x=cos210°+cos250°-sin40°sin80°
⑤
y=sin210°+sin250°+cos40°cos80°
⑥
⑦
由⑤-⑥得:x-y=cos20°+cos100°-cos40°=0
⑧
2 和差型对偶式
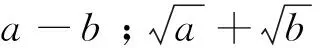
例3 已知a、b、c、d∈R,a2+b2+c2+d2≤1,求证(a+b)4+(a+c)4+(a+d)4+(b+c)4+(b+d)4+(c+d)4≤6.
证明记M=(a+b)4+(a+c)4+(a+d)4+(b+c)4+(b+d)4+(c+d)4,
构造对偶式N=(a-b)4+(a-c)4+(a-d)4+(b-c)4+(b-d)4+(c-d)4.
于是M+N=6(a4+b4+c4+d4+2a2b2+2a2c2+2a2d2+2b2c2+2b2d2+2c2d2)=6(a2+b2+c2+d2)2≤6.
又因为B≥0, 所以A≤6.
3 对称型对偶式
即将A=f(x,y)配以B=f(y,x) ,再通过运算及变形加以解决.
例4 若α、β、γ为锐角,且cos2α+cos2β+cos2γ=1.
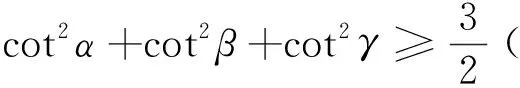
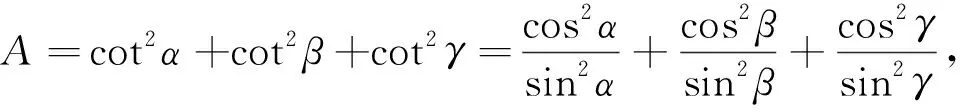
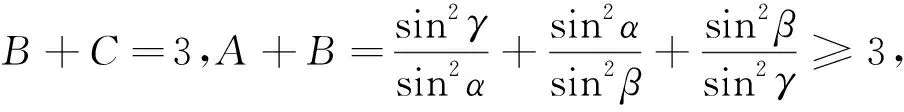
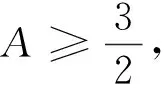
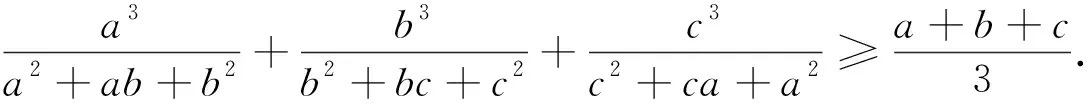
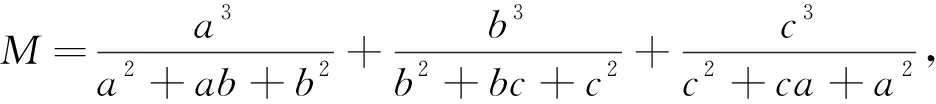
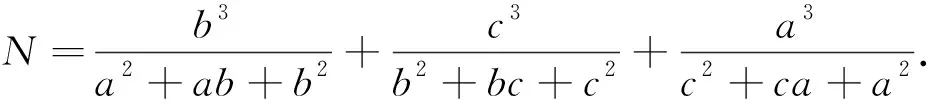
则M-N=(a-b)+(b-c)+(c-a)=0,
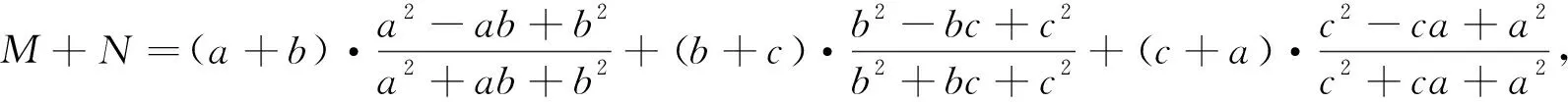
由基本不等式可得:
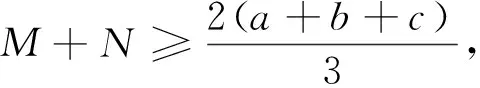
练习题
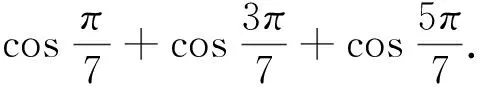
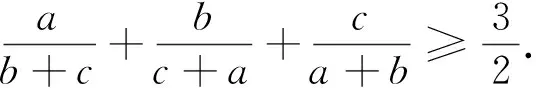
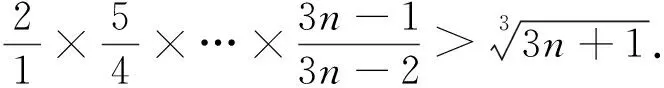
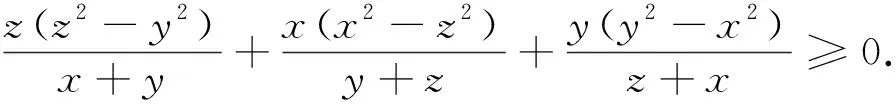
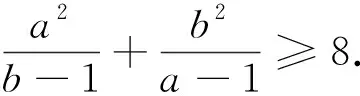
(6)已知a1、a2、…、an均为正数,且a1+a2+…+an=1,