一道2018年全国高中数学联赛福建赛区预赛试题的探究

安徽省淮南第三中学 (邮编：232001)

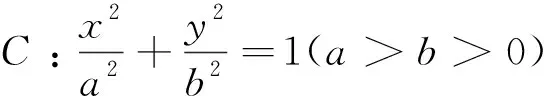
(1)求椭圆C的方程；

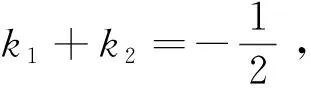
在对该试题进行求解、研究时发现，试题背后蕴含着圆锥曲线一个优美、有趣的性质. 现行文给出，与大家一起分享.

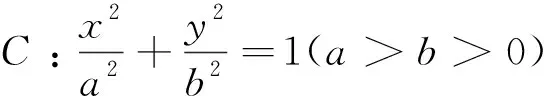
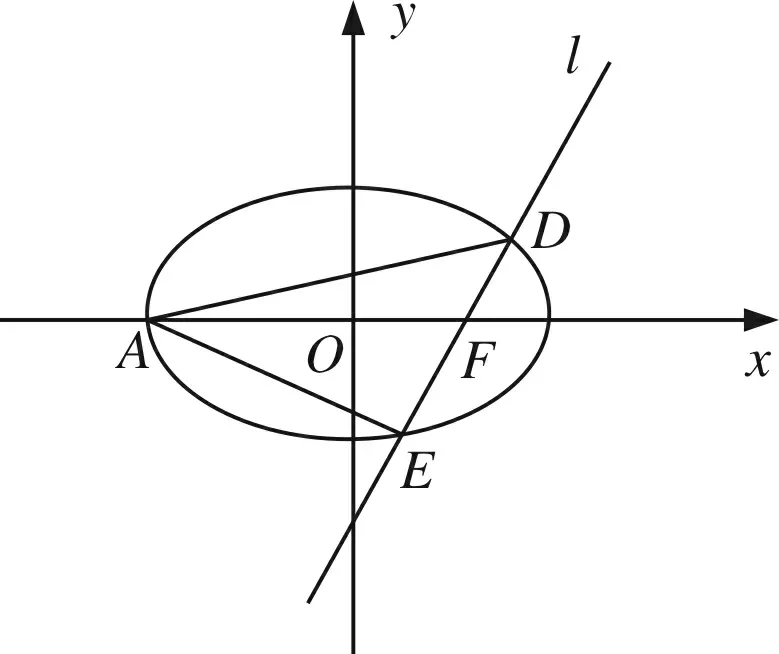
图1

证明如图1，设D点坐标(x1,y1)，E点坐标(x2,y2)，

(a2k2+b2)x2-2a2k2cx+a2(k2c2-b2)=0，

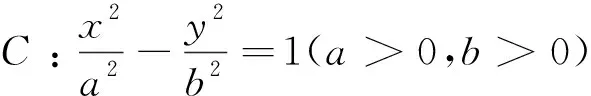
结论3 已知F为抛物线C：y2=2px(p>0)的焦点，过点F且斜率为k的直线l交抛物线C于D、E两点，记直线OD、OE的斜率为k1、k2，则k(k1+k2)=-4.

图2

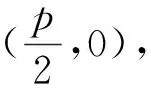
参照结论1的证明，有兴趣的读者可以自己完成结论2的证明.

至此，我们找到了椭圆、双曲线的一个统一性质，也找到了抛物线的一个类似性质. 这些结论不但优美、有趣，其发现过程对高中课堂教学乃至学生数学核心素养的培养都具有一定的启发性.