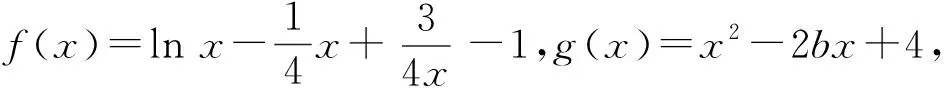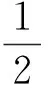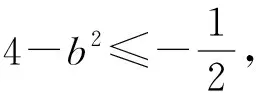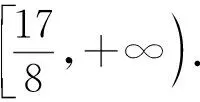双变量的“任意性问题”与“存在性问题”辨析
河北省邯郸市第一中学 (邮编:056000)
含有参数的方程(或不等式)中的“任意性”与“存在性”问题历来是高考考查的一个热点,也是高考复习中的一个难点.破解的关键在于将它们等价转化为熟悉的基本初等函数的最值或值域问题,而正确区分“任意性”与“存在性”问题也是解题的关键.
1 “∀x,使得f(x)>g(x)”与“∃x,使得f(x)>g(x)”的辨析
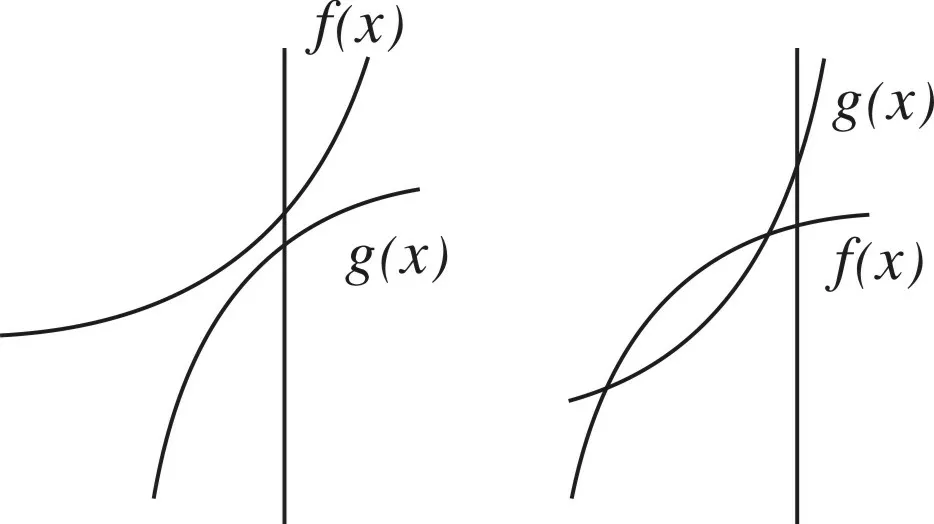
图1 图2
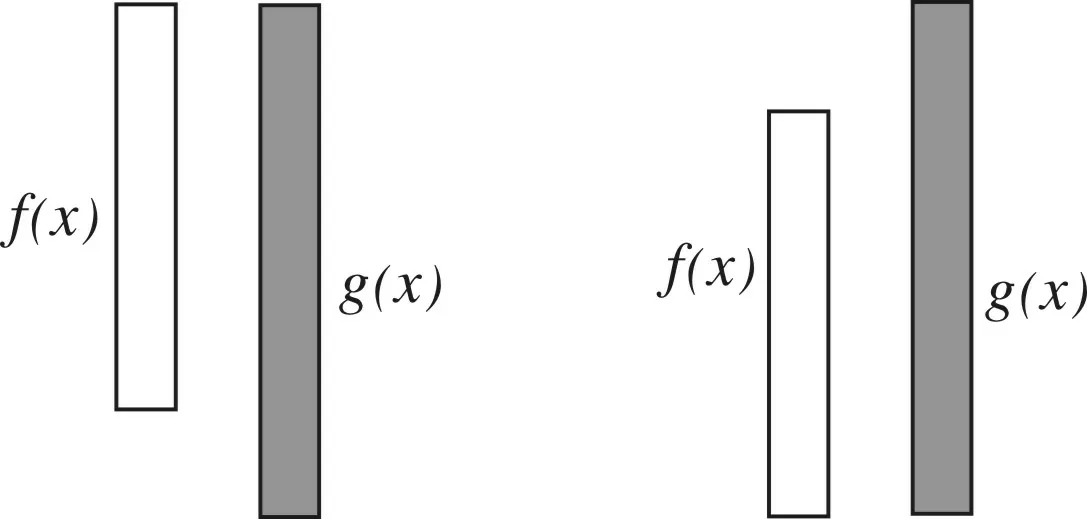
(1)∀x,使得f(x)>g(x),只需h(x)min=[f(x)-g(x)]min>0.如图1.
(2)∃x,使得f(x)>g(x),只需h(x)max=[f(x)-g(x)]max>0.如图2.
例1 设函数f(x)=ln(1+x),g(x)=af′(x),其中f′(x)是f(x)的导函数.
(1)若对于任意x≥0,总有f(x)≥g(x),求实数a的取值范围;
(2)若存在x≥0,使得f(x)≥g(x),求实数a的取值范围.
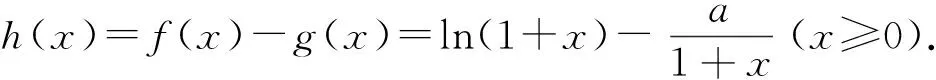
当a≥-1时,h′(x)≥0,h(x)在[0,+∞)上单调递增,
所以,h(x)≥h(0)=-a,则-a≥0,a≤0,
故a∈[-1,0].
当a<-1时,对于x∈(0,-a-1)有h′(x)<0,则h(x)在(0,-a-1)上单调递减,所以h(-a-1)
综上可知,实数a的取值范围为[-1,0].
(2)由(1)可知,当a≥-1时,存在x≥0,使得f(x)≥g(x),
当a<-1时,令x0=e-a-1,则x0>0,
有h(x0)=-a(1+ea)>0,
故必存在x≥0,使得f(x)≥g(x).
综上可知,实数a的取值范围是(-∞,+∞).
点评(1)这是较为常见的一类恒成立问题,运用数形结合的思想可知,当x0≥0时,总有f(x0)≥g(x0),即f(x0)-g(x0)≥0(注意不是f(x)min≥g(x)max),可以转化为当x≥0时,h(x)=f(x)-g(x)≥0恒成立问题.
(2)存在x≥0,使得f(x)≥g(x),即至少有一个x0≥0,满足f(x0)-g(x0)不是负数,可以转化为当x≥0时,h(x)=f(x)-g(x)的函数值至少有一个是非负数.
2 “若∃x1∈D1,∃x2∈D2,使得f(x1)=g(x2)”与“∀x1∈D1,∃x2∈D2,使得f(x1)=g(x2)”的辨析
(1)∃x1∈D1,∃x2∈D2,使得f(x1)=g(x2)等价于函数f(x)在D1上的值域A与g(x)在D2上的值域B的交集不是空集,即A∩B≠∅,如图3.其等价转化的目标是两个函数有相等的函数值.
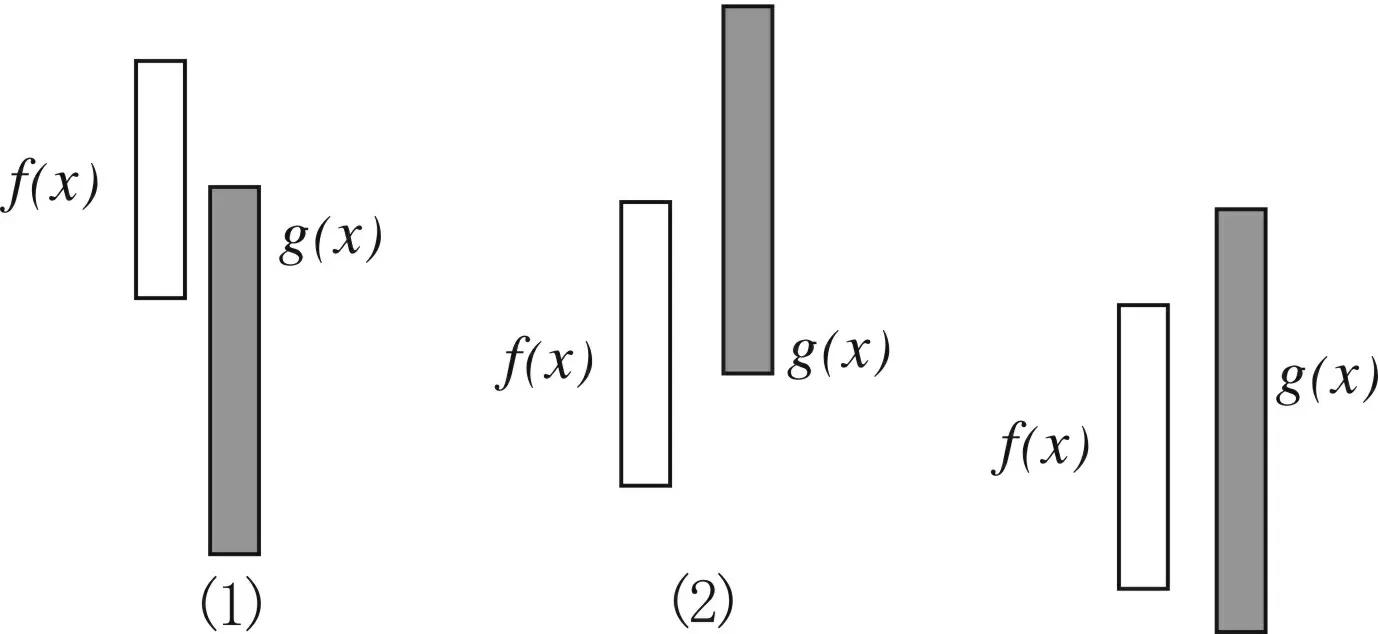
图3图4
(2)∀x1∈D1,∃x2∈D2,使得f(x1)=g(x2)等价于函数f(x)在D1上的值域A是g(x)在D2上的值域B的子集,即A⊆B,如图4.其等价转化的目标是函数y=f(x)的值域都在函数y=g(x)的值域之中.
说明图3,图4中的条形图表示函数在相应定义域上的值域在y轴上的投影.
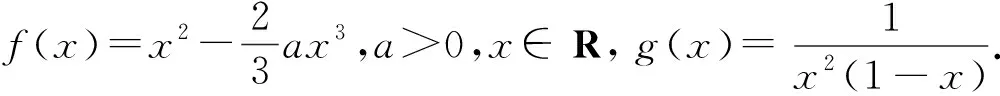
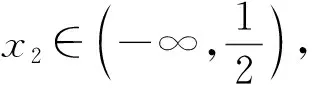
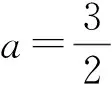
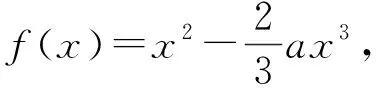
f′(x)=2x-2ax2=2x(1-ax).
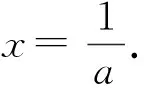
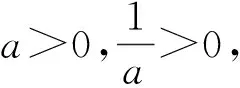
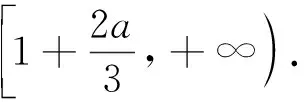
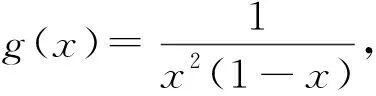
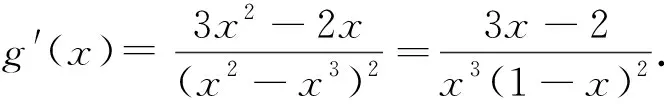
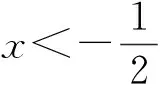
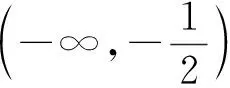
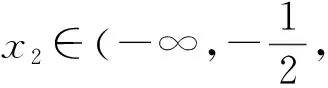
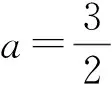
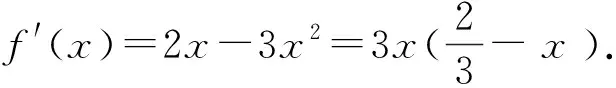
当x>1时,f′(x)<0,所以f(x)在(1,+∞)上单调递减,且f(2)=-4.
所以f(x)在(2,+∞)上的值域为(-∞,-4).
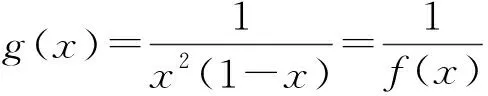
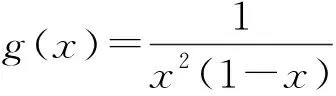
因为(-∞,-4)⊂(-∞,0),
所以对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)=g(x2).
点评本例第(1)问等价转化的基本思想是:两个函数有相等的函数值,即它们的值域有公共部分;第(2)问等价转化的基本思想是:函数f(x)的任意一个函数值都与函数g(x)的某一函数值相等,即f(x)的值域都在g(x)的值域中.
3 f(x),g(x)是闭区间D上的连续函数,“∀x1,x2∈D,使得f(x1)>g(x2)”与“∃x1,x2∈D,使得f(x1)>g(x2)”的辨析
(1)f(x),g(x)是在闭区间D上的连续函数且∀x1,x2∈D,使得f(x1)>g(x2),等价于f(x)min>g(x)max.其等价转化的目标是函数y=f(x)的任意一个函数值均大于函数y=g(x)的任意一个函数值.如图5.
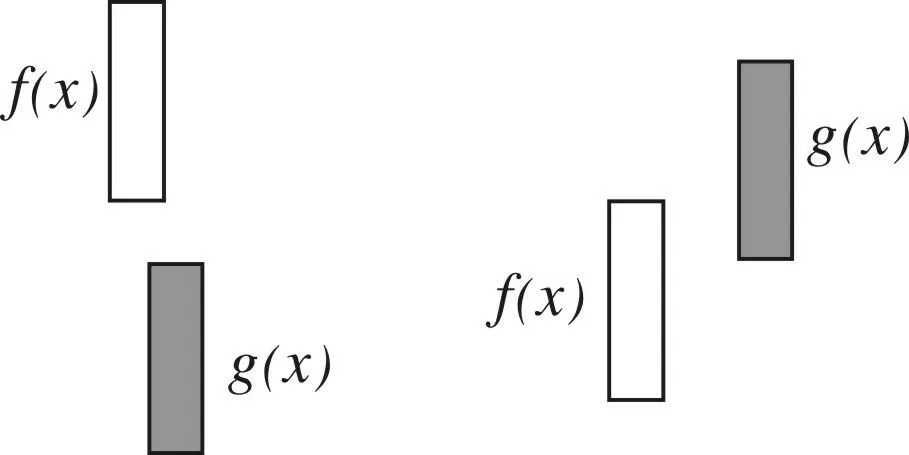
图5 图6
(2)存在x1、x2∈D,使得f(x1)>g(x2),等价于f(x)max>g(x)min.其等价转化的目标是函数y=f(x)的某一个函数值大于函数y=g(x)的某些函数值.如图6.
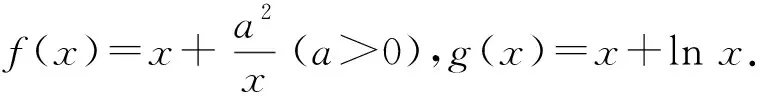
(1)若对任意的x1、x2∈[1,e],都有f(x1)≥g(x2)成立,求实数a的取值范围;
(2)若存在x1、x2∈[1,e],使得f(x1) 解(1)对任意的x1、x2∈[1,e],都有f(x1)≥g(x2)成立,等价于x∈[1,e]时,f(x)min≥g(x)max. 令h(x)=(e+1)x-x2. (2)存在x1、x2∈[1,e],使得f(x1) 当0 当1≤a≤e时,f(x)在[1,a]上单调递减,在[a,e]上单调递增,f(x)min=f(a)=2a, 点评(1)本例第(1)问从数的角度看,问题的本质就是f(x)min≥g(x)max.从形的角度看,问题的本质就是函数f(x)图象的最低点也不低于g(x)图象的最高点. (2)本例第(2)问从形的角度看,问题的本质就是函数f(x)图象的最低点低于g(x)图象的最高点. (1)∀x1∈D1,∃x2∈D2,使f(x1)>g(x2),等价于函数f(x)在D1上的最小值大于g(x)在D2上的最小值,即f(x)min>g(x)min(这里假设f(x)min,g(x)min存在).其等价转化的目标是函数y=f(x)的任意一个函数值大于函数y=g(x)的某一个函数值.如图7. 图7 图8 (2)∀x1∈D1,∃x2∈D2,使f(x1) 解依题意知f(x)在(0,2)上的最小值不小于g(x)在[1,2]上的最小值,即f(x)min≥g(x)min.所以 则当0 当1 又g(x)=x2-2bx+4, 点评“对任意x1∈(0,2),总存在x2∈[1,2],使f(x1)≥g(x2)”等价于“f(x)在(0,2)上的最小值大于或等于g(x)在[1,2]上的最小值”.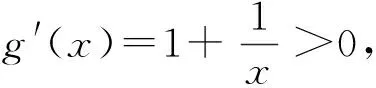
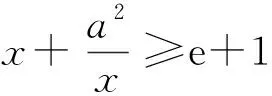
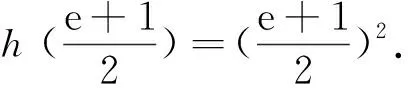
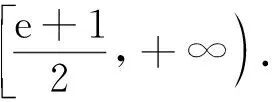
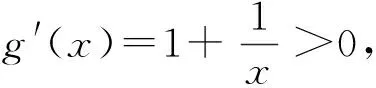
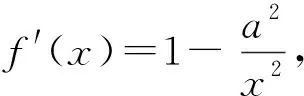
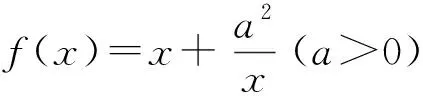
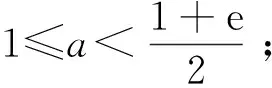
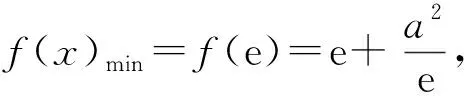
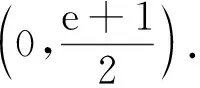
4 “∀x1∈D1,∃x2∈D2,使f(x1)>g(x2)”与“∀x1∈D1,∃x2∈D2,使f(x1)