矩形的一个优美性质及其应用

湖北省阳新县高级中学 (邮编：435200)

本文向读者介绍矩形的一个优美性质，并从几何、代数、向量等角度给出多种证法，最后举例说明性质在解决有关数学问题中的应用.

1 矩形的一个优美性质

性质矩形所在平面内任意一点到不相邻的两个顶点的距离的平方和相等.

已知：点P是矩形ABCD所在平面内任意一点，求证：PA2+PC2=PB2+PD2.

图1 图2

矩形的这一性质文字简洁精准，图形方正大方，等式对称优美.下面给出多种证法.

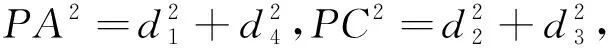
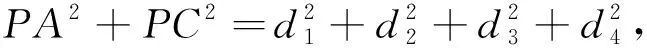
故PA2+PC2=PB2+PD2.

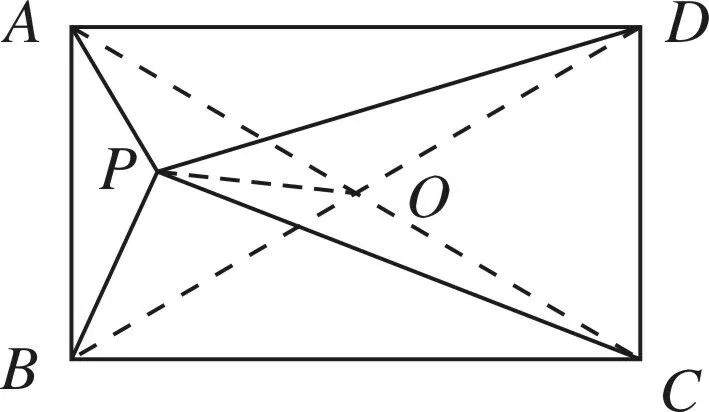
图3 图4

证法2 (用三角形中线长公式)如图3、图4，在△PAC中，O为AC中点，由三角形中线长公式得PA2+PC2=2(PO2+OA2).在△PBD中，O为BD中点，由三角形中线长公式得PB2+PD2=2(PO2+OB2).又OA=OB，所以PA2+PC2=PB2+PD2.

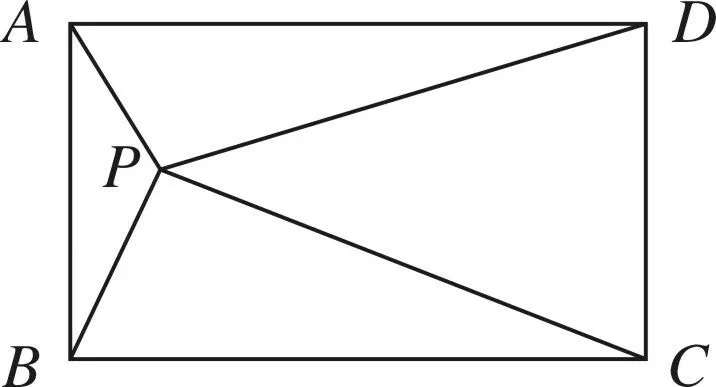
图5

图6

证法4 (坐标法)建立直角坐标系如图6所示，设BC=a,AB=b，设点P的坐标为(x,y).由两两点间的距离公式得

PA2+PC2=x2+(y-b)2+(x-a)2+y2，PB2+PD2=x2+y2+(x-a)2+(y-b)2.

所以PA2+PC2=PB2+PD2.

评注证法1和证法2为几何证法，需要添加辅助线，同时还要对点P与矩形的位置关系进行分类讨论，证法3向量证法和证法4坐标证法，不需要添加辅助线，也不需要分类讨论，充分体现了向量法与坐标法的优越性，其中坐标证法非常简洁.

2 性质应用举例

例1 在平面直角坐标系xOy中，已知定点P(1,-1)，圆C1:x2+y2=5和圆C2:x2+y2=8，M,N是C1上的两个动点，Q是C2上的动点，则四边形PMQN能构成矩形的个数是( )

A.0个 B.2个 C.4个 D.无数个

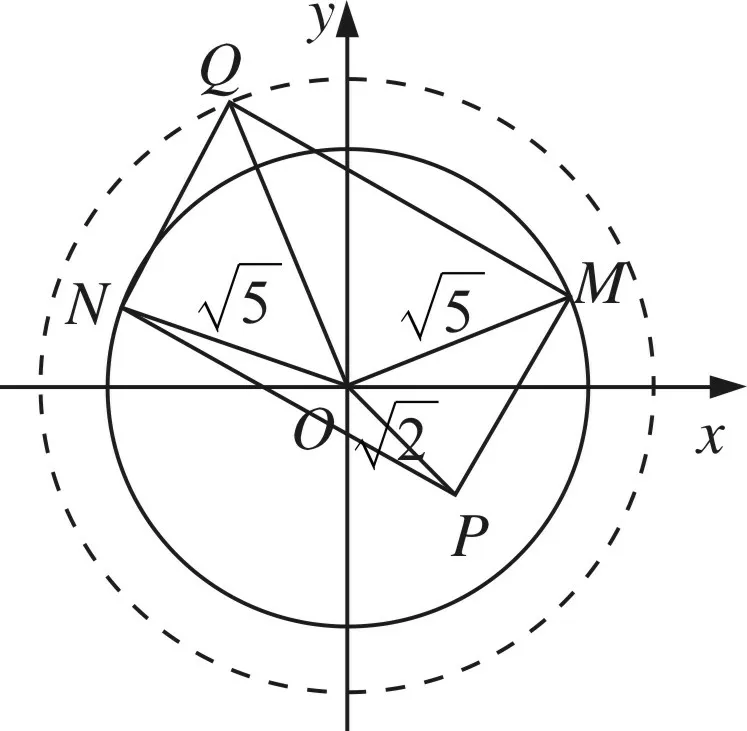
图7

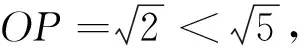
满足条件的矩形可这样得到：在圆C1上任意取一点M，连接PM，过点P作PM的垂线交圆C1于点N，过点M,N分别作PN,PM的平行线相交于点Q，则四边形PMQN就是点Q在圆C2上的矩形.

例2 (2013年高考重庆卷理科第10题)在平面上，

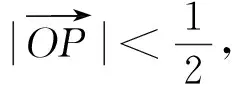
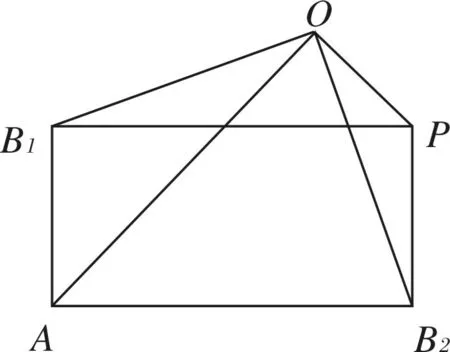
图8

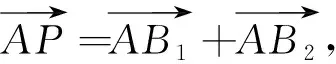
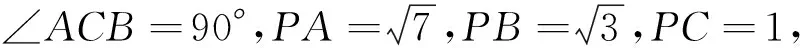
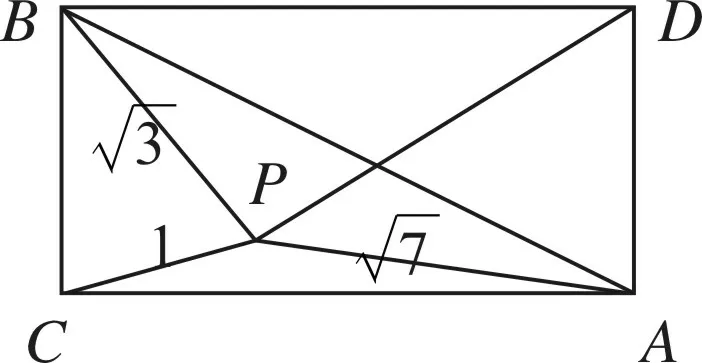
图9

解如图9，以CA,CB为邻边作矩形CADB.

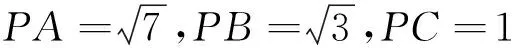
故AB的取值范围是[2,4].

(1)证明：点B的轨迹是一个圆，并求出圆的半径；

(2)证明：线段PQ的中点M轨迹也是一个圆，并说明圆心的位置求出半径大小.

解(1)如图10，以AP,AQ为邻边作矩形APBQ.由矩形性质得OA2+OB2=OP2+OQ2，将

代入得OB=3.故B的轨迹是以点O为圆心以3为半径一个圆.

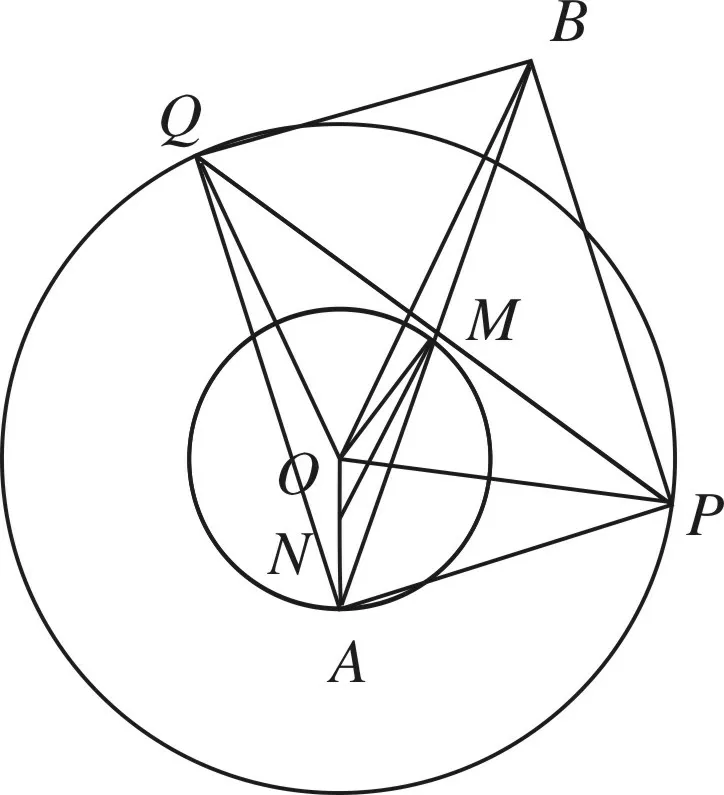
图10

(2)取OA中点N，连接MO,MN,MA.OP=OQ,MP=MQ，所以OM⊥PQ，由勾股定理得MP2+MO2=OP2=5.又AM是直角△PAQ斜边上的中线，所以MA=MP，于是MA2+MO2=5.

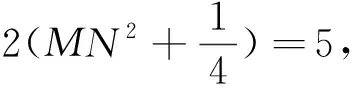
点评本题第1问用矩形性质证明，第2问是用三角形中线长公式证明的，由矩形性质证法2知，矩形性质也可用三角形中线长公式证明.运用定理结论以及运用定理证明时所用到的定理公式和方法去解决新的数学问题同样重要，务必引起重视.