关于哈林图的邻和可区别染色的注记

程银万, 杨 超, 姚 兵

(1. 上海工程技术大学 数理与统计学院, 智能计算与应用统计研究中心, 上海 201620;2. 西北师范大学 数学与统计学院, 兰州 730070)

1 引言与预备知识

本文考虑的图G=(V,E)均为简单、 无向、 连通图.设[n]表示正整数集合{1,2,…,n},dG(v)和δ(G)分别表示一个点v的度和图G的最小度.用NG(x)或N(x)表示图G中顶点x的邻点集合.本文涉及的其他概念可参见文献[1].

猜想1[2]对于阶数至少为3的任意连通图G, gndi∑(G)≤3.

Kalkowski等[3]证明了若G是k-可着色的且k为奇数, 则G中存在一个邻和可区别k-边染色.因此, 对于一类3-可着色图, 包括二部图, 猜想1成立; Addario-Berry等[4]给出了当k=30时, 每个无孤立边的图都有一个邻和可区别k-边染色; 进一步， 文献[5]和文献[6]分别将k值改进到k=15和k=13; 对于每个无孤立边的图, Kalkowski等[3]还证明了其都是邻和可区别5-边染色的; Przybylo[7]证明了每个d-正则图(d≥2)都是邻和可区别4-边染色的, 且当d≥108时, 每个d-正则图都是邻和可区别3-边染色的.

Przybylo等[8]在邻和可区别边染色的基础上考虑加上点自身的颜色, 定义了图的邻和可区别全染色.设f:V(G)∪E(G)→[k]为图G的一种非正常k-全染色.对于每个顶点x, 设

t(x)=f(x)+σ(x).

如果图G中的任意相邻顶点x和y满足t(x)≠t(y), 则称f为图G的一个邻和可区别全染色(NSDT).图G的NSDT-k-全染色中最小值k称为图G的邻和可区别全色数, 记为tgndi∑(G).进一步, Przybylo等[8]给出了关于邻和可区别全染色的1-2猜想:

猜想2[8]对于任何连通图G, tgndi∑(G)≤2.

当图G是一个3-可着色图、 完全图或者4-正则图时[8], 猜想2成立.Kalkowski[9]给出了一个较理想的结果: 对于每个图G, tgndi∑(G)≤3.Flandrin等[10]考虑将顶点的颜色加入到其邻点和邻边的权重和中, 提出了图的邻点全和可区别全染色.

设f:V(G)∪E(G)→[k]表示图G的一个非正常k-全染色.定义权重函数

如果对任意边xy∈E(G), 都有φ(x)≠φ(y), 则称f为图G的一个邻点全和可区别k-全染色(NFSD).图G的NFSD-k-全染色中最小值k称为图G的邻点全和可区别全色数, 记为fgndi∑(G).

设T是至少有4个顶点的树, 则树T中的顶点或者是度为1的点(称为叶子), 或者是度至少为3的点.哈林图H=T∪C是用圈C顺次连接树T中的所有叶子而得到的一类平面图.通常称T为哈林图的特征树,C称为其伴随圈.设V0⊆V(H)V(C), 且V0中的每个点均与圈C上的顶点相邻.设V1是V0的子集, 且满足V1中每个顶点的邻边中(dG(v)-1)条邻边与叶子相连.

本文先对特征树T进行边染色, 并给伴随圈C的边分配颜色, 证明1-2-3猜想对哈林图成立; 再对特征树T进行全染色, 并给伴随圈C的边E(C)分配颜色, 证明1-2猜想对哈林图也成立； 最后对特征树T进行全染色, 并给伴随圈C的边E(C)进行调色, 得到哈林图的邻点全和可区别全色数至多为3.

2 哈林图的1-2-3猜想

算法1

步骤1) 对树T的边染色定义如下两种染色方式.

f1(ev): 对顶点v的所有未染色邻边分配颜色3;

f2(ev): 对顶点v的未染色邻边之一分配颜色2, 其余邻边都染颜色3.

步骤2) 选择点集V1中一个最小度点并标记其为v.初始地, 对v与叶子相邻的一条边染颜色2,v的其余邻边都染颜色3.

步骤3) 设vi是顶点v的邻点.如果点vi度的奇偶性与点v度的奇偶性不同, 则采用染色方式f2(evi)对vi邻边进行染色; 否则, 采用染色方式f1(evi).

步骤4) 设vij是顶点vi的邻点.当σ(vi)=3dH(vi), 且点vij度的奇偶性与点vi度的奇偶性不同时, 采用染色方式f1(evij)对vij的邻边进行染色; 否则, 采用染色方式f2(evij).

当σ(vi)=3dH(vi)-1,f(vivij)=2, 且点vij度的奇偶性与点vi度的奇偶性不同时, 采用染色方式f1(evij); 否则, 采用染色方式f2(evij).如果f(vivij)=3, 且点vij度的奇偶性与点vi度的奇偶性不同时, 则采用染色方式f2(evij); 否则, 使用染色方式f1(evij).

步骤5) 设vijk是顶点vij的邻点.当σ(vij)=3dH(vij), 且点vijk度的奇偶性与点vij度的奇偶性不同时, 采用染色方式f1(evijk)； 否则, 采用染色方式f2(evijk).

当σ(vij)=3dH(vij)-1,f(vijvijk)=2, 且点vijk度的奇偶性与点vij度的奇偶性不同时, 采用染色方式f1(evijk)； 否则, 采用染色方式f2(evijk).如果f(vijvijk)=3, 且点vijk度的奇偶性与点vij度的奇偶性不同时, 则采用染色方式f2(evijk)； 否则, 采用染色方式f1(evijk).

当σ(vij)=3dH(vij)-2,f(vijvijk)=2, 且点vijk度的奇偶性与点vij度的奇偶性不同时, 采用染色方式f2(evijk)； 否则, 采用染色方式f1(evijk).如果f(vijvijk)=3, 且点vijk度的奇偶性与点vij度的奇偶性不同时, 则采用染色方式f1(evijk)； 否则, 采用染色方式f2(evijk).

步骤6) 继续上述过程, 直到T中所有的边都被分别标注2和3.

定理1设H=T∪C为哈林图, 则gndi∑(H)≤3.

证明: 首先利用算法1证明可以用颜色2和3完成对任意树T的邻和可区别边染色.

设Cm=x1x2…xmx1是伴随圈.xiyj是边集E(H)中的边, 其中xi∈V(Cm),yj∈V0, 1≤i≤m, 1≤j≤|V0|, 且下标i和j分别表示对m和|V0|取模.由算法1知, 树T中所有相邻点权重的奇偶性不同.对于点集V0中的任意顶点yj,yj的所有与叶子相连的边最多只有一条染了颜色2.因此, 通过交换v的邻边中与叶子相邻边的颜色, 可达到边x2k+1yj都染颜色3的效果, 且点v权重不发生变化, 其中0≤k≤(m-1)/2.然后, 将圈Cm上所有的边都染颜色1.由于点集V0中任一顶点可能的最小度是3, 故满足σ(yj)≥7, 且xi最大的权重是5.因此σ(yj)≥σ(xi)总成立.下面根据两种情形区别圈Cm上两个相邻顶点xi和xi+1的权重.

情形1)m≡0(mod 2).将边x2k+1yj的颜色从3变为1,x2k+1的权重变为3, 且x2k的权重是4或5.同时,V0中所有顶点的权重值都会减少2的整数倍, 因此V0中所有顶点权重的奇偶性仍未变, 树T中相邻顶点的权重依然是可区别的.在这种情形下,σ(yj)的最小权重将会减少到5, 但与yi相邻的顶点xi的权重会减少到3或4, 且它们的权重值总小于σ(yj).在该情形下， 哈林图的一种邻和可区别边染色如图1(A)所示.

情形2)m≡1(mod 2).设圈C上的点x1和xm是v的两个相邻点, 且v∈V1.类似地, 将边x2k+1yj的颜色从3变为1.此时,σ(x2k+1)=3,σ(x2k)=4或5, 但x1和xm的权重都是3.显然, 算法1中对树染色时, 顶点v的邻边有一条与叶子相连的邻边染了颜色2, 将该边标记为xmv.此时,σ(v)=3dH(v)-1,σ(vi)=3dH(vi) 或3dH(vi)-1,vi∈V(H)V(C).当xm-1的权重是5时, 保持边xmv的颜色2 不变以保证σ(xm)=4.经上述调色,V0中所有顶点权重的奇偶性均不变.如果d(v)=3且σ(xm-1)=4, 则将边xmv的颜色从2变为1, 将xmxm-1的颜色从1变为2, 且σ(xm)=4,σ(xm-1)=5.此时,σ(v)的权重变为5, 但σ(x1)=3且σ(xm)=4, 所以它们的权重依然是可区别的, 且vi的最小权重为9, 大于σ(v).在该情形下， 哈林图的一种邻和可区别边染色如图1(B)所示.证毕.

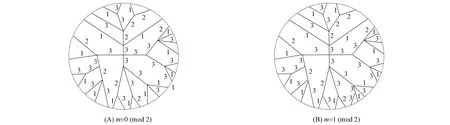
图1 两类哈林图的邻和可区别3-边染色(伴随圈上的边均染颜色1)Fig.1 Neighbor sum distinguishing 3-edge coloring of two types of Halin graphs (edges on adjoint cycle are colored by 1)

3 哈林图的1-2猜想

算法2

步骤1) 树T中所有边染颜色2且所有叶子染颜色1.

步骤2) 选择点集V1中一个最小度点并标记其为v.初始地, 用颜色1染点v.

步骤3) 设vi是点v的非叶子邻点, 用颜色2染所有的顶点vi.

步骤4) 设vij是点vi的非叶子邻点, 用颜色1染所有的顶点vij.

步骤5) 重复步骤2)和步骤3), 直到T中的所有点都染了颜色1或2.

定理2设H=T∪C为哈林图, 则tgndi∑(H)≤2.

证明: 首先, 假设树T中所有的边均染了颜色2, 树T中的各个顶点用颜色1或2染色.则可使用颜色1和2完成对树T的邻和可区别全染色.算法2已证明上述染色是可行的.

由算法2知, 除叶子外, 所有相邻顶点权重的奇偶性均不同.V0中所有顶点的可能最小度为3, 且满足t(xi)=3及t(yj)≥7.圈Cm上所有的边染颜色1, 可得叶子xi的权重值都是5.下面通过两种情形调整点xi的染色.

情形1)m≡0(mod 2).将点x2k+1的染色从颜色1变为2, 则x2k+1的权重即从5变为6.但点x2k的权重依然是5.所以t(yj)>t(xi)仍成立.

情形2)m≡1(mod 2).将点x2k+1的颜色从颜色1变为2, 则x2k+1的权重从5变为6.此外, 仍需改变一些点和边的染色如下:f(xm)=f(xmv)=1,f(v)=2.xm的权重即为4, 不同于所有邻点的权重值, 且v的权重仍未改变.证毕.

4 哈林图的NFSD-全染色

算法3

步骤1)T中每个顶点染颜色1.

步骤2) 选择点集V1中一个最小度点并标记其为v.初始地, 对v所有邻边都染颜色3.

步骤3) 设vi是点v的邻点.将点vi的其中一条邻边染颜色2, 其余邻边都染颜色3.

步骤4) 设vij是vi的邻点, 对点vij的邻边按如下方式染色:

①f(vivij)=2, 将vij的一条未染色邻边标注颜色2, 剩余的vij所有邻边都染颜色3;

②f(vivij)=3,vij的所有邻边都染颜色3.

步骤5) 设vijk是vij的邻点, 按以下方式标记点vijk的邻边:

①φ(vij)=4dT(vij)+1, 用颜色2染点vijk的一条未染色邻边, 点vijk剩余的邻边都染颜色3;

②φ(vij)=4dT(vij)-1, 当f(vijvijk)=3时, 用颜色2染点vijk的一条未染色邻边,vijk剩余的邻边都染颜色3, 当f(vijvijk)=2时,vijk的所有邻边都染颜色3.

步骤6) 重复步骤4)和步骤5), 直到树T完成邻点全和可区别全染色.

定理3设H=T∪C为哈林图, 则fgndi∑(H)≤3.

证明: 首先证明用3种颜色即可完成对树T的一个邻点全和可区别全染色, 染色方案为:T中所有的顶点都染颜色1,T中的边染颜色2或3.算法3已证明所给染色方案是可行的.

设Cm=x1x2…xmx1表示伴随圈.xiyj是边集E(H)中的边, 其中xi∈V(Cm),yj∈V0, 1≤i≤m, 1≤j≤|V0|, 且下标i和j分别表示对m和|V0|取模.由算法3可知, 相邻顶点的权重奇偶性不同.对于V0中的任意顶点v, 其邻点vxi的邻边中最多只有一条边染颜色2.

情形1)m≡0(mod 2).将边x2k+1yj的颜色从3变为1, 所有顶点x2k+1的权重都是7且x2k的权重是8或9.同时,V0中所有顶点的权重减少了2的整数倍, 因此V0中各顶点权重的奇偶性不变.在这种情形下,φH(yj)的最小值将减少为9, 但xi或yi邻点xi的权重是7或8, 仍然不同于φH(yj).

情形2)m≡1(mod 2).设x1和xm为圈C上v的两个相邻顶点且v∈V1.改变边x2k+1yj的颜色, 从3变为1.因此,φ(x2k+1)=7,φ(x2k)=8或9, 但x1和xm的权重相同, 均为7.显然,v的所有邻边均染颜色3, 且φ(v)=4dH(v)+1,φ(vi)=4dH(vi),vi∈V(H)V(C).当xm-1的权重为8时, 将边xmv的颜色从颜色1变为3, 使得φ(xm)=9.经过上述染色,V0中所有顶点权重的奇偶性仍然不变.如果φ(xm-1)=9,d(v)≥4, 将边xmxm-1的染色从颜色1变为2, 则φ(xm)=8且φ(xm-1)=10.此时,φ(v)的奇偶性未变.同时,φ(v)≥13总成立.当d(v)=3时, 将边xmv的颜色从1变为2, 可得φ(xm)=8，φ(v)变为10.但当vi的度为3时,vi的最小权重是12.

对任意特征树T采用算法3以及对伴随圈上的边进行调色后, 可得哈林图邻点全和可区别3-全染色.证毕.