一种循环多尺度的图像盲去模糊网络
张玉波, 王建阳, 韩 爽, 王冬梅
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
图像去模糊即从一张模糊图像中复原该图像的纹理细节, 使其清晰化[1]. 在深度学习算法普及前, 图像去模糊一般采用去卷积操作, 严重依赖于对模糊核的计算. 传统去模糊算法目前已有许多, 如Xu等[2]提出了一种基于空间先验和迭代支持检测核精化的两阶段模糊核估计方法, 利用去卷积模型进行盲去模糊; Sun等[3]提出了补丁先验的方法, 利用自然图像中提取的边缘图像块作为先验信息, 约束图像间的相似性, 生成高质量的图像; Xu等[4]利用L0稀疏先验提出了一种有效的去模糊方法, 该方法可在少量迭代中迅速收敛, 有较快的运行时间与较好的图像质量; Zhang等[5]提出了利用先验知识抑制图像处理中的伪影, 提升了复原图像的清晰度; Pan等[6]针对文本图像去模糊提出了一种基于L0正则化先验的方法, 可对低照度文本图像进行有效的去模糊; Yan等[7]提出了一种极致通道先验(extreme channels prior)方法, 基于亮通道先验联合暗通道先验, 进一步提升了图像去模糊的效果与算法的稳定性. 但由于传统的模糊模型依赖于图像的先验知识[8], 因此尽管在一些专用领域表现出优异的性能, 但在面对多种因素导致的模糊时, 通常泛化性较差.
近年来, 深度学习框架在图像去模糊中得到广泛应用, 获得了较好的效果. 该类算法通过有效地学习原始图像与模糊图像之间的对应关系执行去模糊操作. Sun等[9]使用该类技术反向计算出图像的模糊核, 然后利用其进行复原; Nah等[10]搭建了一种从粗到细的多尺度卷积框架对图像进行去模糊, 在使用视频合成的真实模糊图像上取得了优异的成绩; Tao等[11]根据金字塔逐步恢复不同尺度原始图像的策略, 提出了一种尺度循环卷积网络的编解码结构, 不同尺度的子网络共享参数, 从粗到精的端到端去模糊; Noroozi等[12]使用融合多个分辨率特征的金字塔结构与短跳连接构建去模糊网络; Gao等[13]提出了PSS-NSC网络, 使用跨层连接和网络参数共享机制, 确保了网络可以自动识别到各尺度下最重要的特征; Cai等[14]使用一种明暗通道先验框架, 通过将明暗通道先验嵌入卷积层中, 取得了较好的去模糊效果; Kupyn等[15]设计了一个新的图像去模糊网络, 通过条件生成对抗网络(GAN)进行去模糊, 与一般的深度学习方法相比, 增加了处理速度; 此后, Kupyn等[16]又搭建了一种具有双鉴别器的GAN网络, 在框架中使用特征塔形结构, 由于该框架使用了最新的轻量化网络, 使得其较其他经典网络计算速度更快; Gong等[17]搭建了一种可进行自学习的去模糊GAN框架, 该框架在处理图像的小范围模糊去除上获得了较理想的结果; Lu等[18]提出了解缠网络分离图像的语义和特征, 通过将模糊特征编入网络提升网络的处理能力.
传统的图像去模糊方法通常先对模糊核进行估算, 通过计算分析得到大致的模糊核后, 再将问题简化为模糊核已知的反向卷积数学问题. 而该方法的缺陷是无法对多模糊核的数据集进行有效拟合, 使得该类方法应用范围较单一. 而深度学习算法庞大的网络层提供了强大的拟合能力, 使其可解决这类缺陷, 但越来越多的网络层叠加也使得网络的参数几何倍增, 在网络结构上较庞大, 且损失函数通常较单一, 生成对抗网络类的算法虽然通常速度较快, 易于训练[19], 但效果一般, 稳定性较差. 因此, 本文提出一种基于循环多尺度的图像盲去模糊网络, 采用从低尺度到高尺度的方法逐步恢复图像, 利用参数共享机制在避免参数过多的同时对图像进行由粗到细的处理. 通过嵌入通道注意力的残差通道选择模块和图像特征跨层直连加强网络的去模糊性能, 所设计的损失函数可综合计算图像的亮度、 结构对比度及均方误差, 以提升去模糊后图像的真实性. 实验结果表明, 在指标与图像主观对比上, 本文算法优于其他经典的图像盲去模糊网络, 具有较稳定的图像去模糊性能.
1 去模糊网络设计
1.1 图像退化模型
图像在生成、 获取、 拷贝和存放过程中, 由于拍摄环境较差, 相机硬件损坏或频繁存取压缩图像等会导致其出现细节失真等问题, 而模糊图像不利于图像识别、 卫星测绘和案件侦破等实际应用, 因此需要对已获得的模糊图像进行去模糊处理.
由图像模糊原理可建模为
B=I⊗K+N,
(1)
其中I为原清晰图像,K为模糊核, ⊗为卷积操作,N为加性噪声.模糊图像可被视为原始图像与模糊核先进行卷积操作, 然后在加性噪声N的影响下生成的.图像去模糊的方法则根据模糊核是否已知分为盲去模糊和非盲去模糊两类.盲去模糊在模糊核未知的情况下进行, 而现实生活中图像产生模糊的原因常复杂多变, 模糊核很难通过计算得出.因此研究盲去模糊问题, 对于如何从真实场景中复原清晰图像具有重要意义.
1.2 网络结构
在网络模型上, 本文采用端到端的卷积神经网络结构[20]作为网络的主要设计思想.为增强网络的去模糊能力, 充分利用图像自身的多尺度信息, 在网络主体结构上, 采用SRN网络[11]的类U-Net结构进行图像的尺度循环处理, 如图1所示. 首先对原始图像进行下采样, 再送入到主框架中开始去模糊处理, 然后将重建去模糊后的清晰图像进行上采样升尺度, 再次输入网络进行循环训练. 循环训练可保持参数的一致性, 由于同一张图像的不同尺度具有相似的模糊特征, 因此, 参数共享机制可以充分发挥神经网络的去模糊能力, 并降低网络的参数量. 在神经网络中, 图像在网络中循环的次数与初始时图像缩小的尺度级别相匹配, 并最终通过多尺度的去模糊循环处理, 使图像具有不同尺度的细粒度特征, 达到较好的去模糊效果.
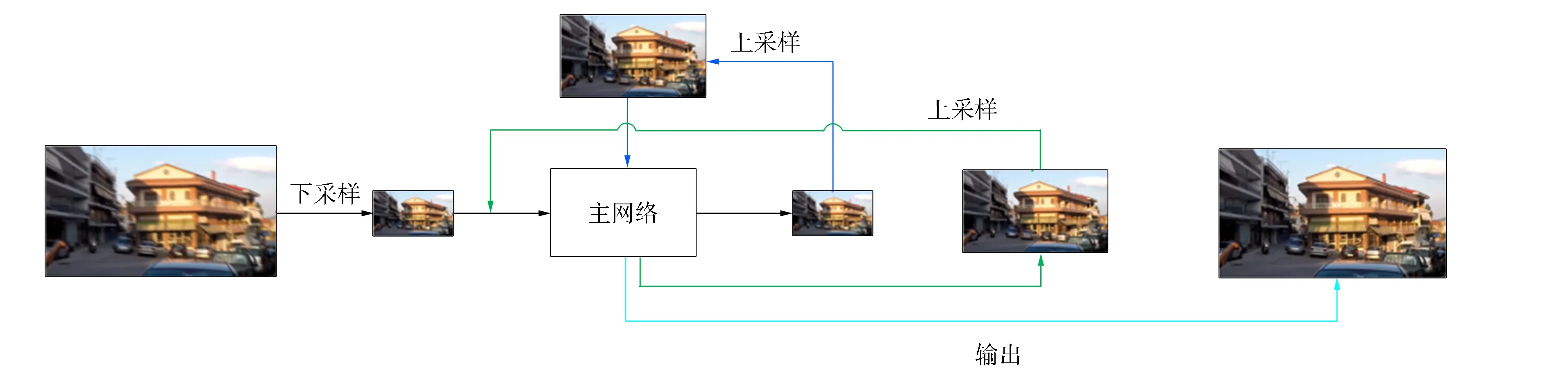
图1 尺度循环示意图Fig.1 Schematic diagram of scale cycle
网络的主体框架如图2所示. ResNet[21]中的跳跃连接设计可实现不同层级特征的引入, 并优化网络训练, 同时受文献[16]在DeblurGANV2网络中长链接设计的启发, 本文在网络中设计了从模糊图像到重建图像的跳跃直连. 通过将原始特征引入至网络输出, 实现图像特征的充分融合. 跳跃长连接可使融合后的图像获得更理想的图像视觉细节, 如图像的光影、 色彩等.
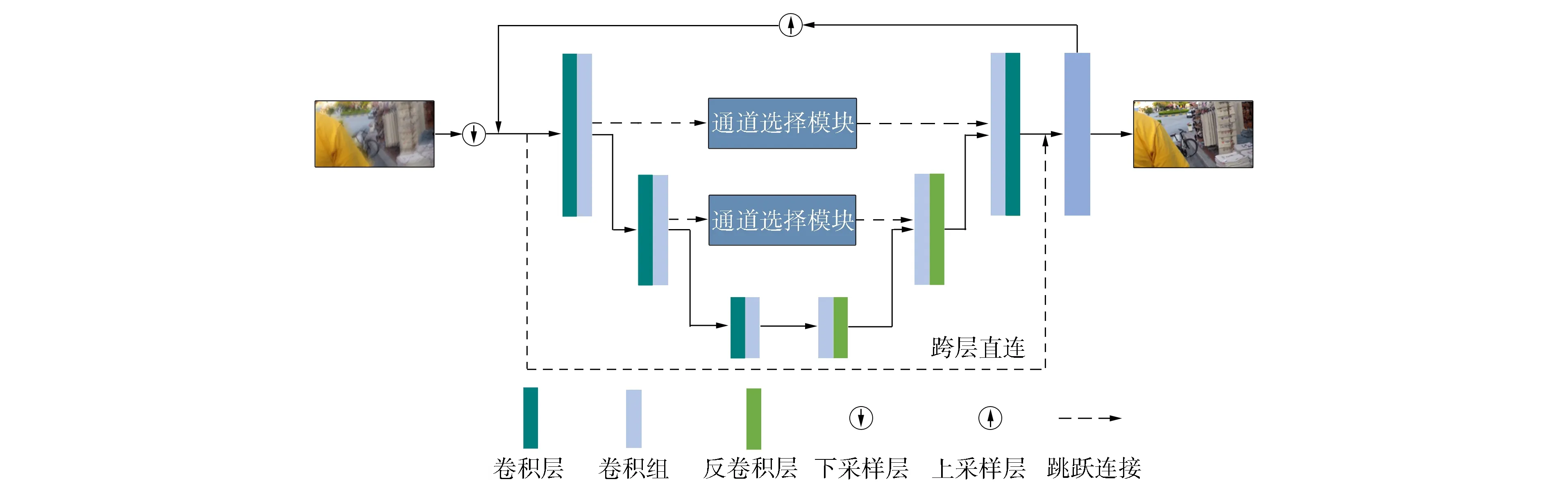
图2 网络主框架Fig.2 Main framework of network
在解码器中, 为增强网络的特征提取能力, 需使用基本卷积结构对网络进行加深. 如图3所示, 类似SRN网络的设计[11], 在网络内部逐层特征提取的卷积层后, 使用3层堆叠的ResNet块, 6组卷积层的卷积组强化特征提取. 在3个不同深度层级的卷积组中, 通道数分别设为32,64,128, 以逐级深化特征. 解码器网络结构采用与编码器一致的对称设计.

图3 卷积组Fig.3 Convolution group
受ResNet残差思想的启发, 本文在神经网络内部采用跳跃连接进行特征的强化传播. 为充分对编码网络的各通道特征进行选择, 本文设计了残差通道选择模块, 如图4所示. 模块内部采用通道注意力[22]的结构, 但不同于经典的通道注意力模型. 由图4可见, 本文在其基础上引入了残差思想, 在进行通道选择的同时保留了原始特征, 以增强网络的去模糊能力.

图4 通道选择模块Fig.4 Channel selection module
1.3 损失函数
为实现对网络的优化训练, 本文设计使用的损失函数为均方误差(mean square error, MSE)和结构相似性(structural similarity, SSIM)的多尺度组合, 可表示为

(2)
其中α为权重系数, 通过实验进行确定.最终的损失将由3个分辨率尺度进行计算并求和得出.
为解决图像盲去模糊算法在结构亮度等细节上优化无力的情况, 本文设计了多尺度结构相似性损失, 其中结构相似性定义为
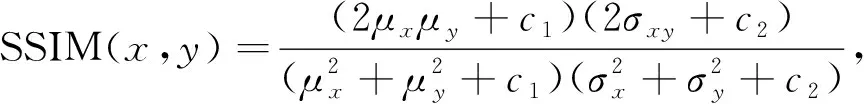
(3)
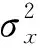
结构相似性综合计算了模糊图像与清晰图像像素级别的亮度、 对比度和结构差异, 将图像均值作为图像亮度的近似, 使用标准差表示图像的对比度, 图像结构则采用协方差度量.当使用两张完全一样的图片时, SSIM值应为1; 当相似度趋近无穷小时, SSIM值则趋近于0. 由于SSIM与MSE在图像训练中的优化方向相反, 因此在拟合MSE的最小值时, SSIM值会增大. 为将其用于损失函数优化, 需对其进行再设计. 因此, 本文采用1-SSIM作为损失函数, 并综合计算3个尺度的图像相似值求和, 在训练过程中将其最小化. 同时, 考虑到单独使用SSIM可能会导致训练方向对光影结构进行过度拟合, 因此本文采用MSE均方误差弥补SSIM作为损失函数时对训练产生的误差, 使训练方向朝像素级的去模糊进行. MSE计算公式为
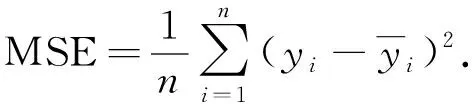
(4)
MSE通过计算去模糊图像与真实图像之间像素级别的差异, 结合SSIM对亮度、 对比度和结构共同对网络训练进行指导. 在训练过程中, 网络将在3个尺度计算模糊图像与真实图像之间的差值并加权相加, 将计算和作为最终损失进行最小化, 从而指导函数收敛. 在本文算法中, 通过多次实验验证, 当多尺度SSIM损失的参数α=0.04时, 可获得较平衡的训练效果. 而在其他图像复原任务中, 对两种损失函数的比重进行微调可获得更优的效果.
2 实 验
2.1 实验数据集
模糊数据集GoPro[10]使用GoPro运动摄影机拍摄的高清图像, 并利用影像临近帧合成真实模糊图, 使用临近帧的中间帧表示清晰图像, 构建了大量的清晰-模糊图像对. 本文采用其中3 214对图像进行实验, 其中2 103对用于网络训练, 1 111对用于结果测试.
为测试网络的有效性与稳定性, 本文使用数据集Kohler[23]进一步进行指标对比. 数据集Kohler由4张图片在12种不同类型的卷积核上卷积而成, 由于模糊核种类较多, 模糊形成复杂, 因此可测试网络的去模糊性能. 本文采用真实数据集Lai[24]进行直观视觉对比, 该数据集包括文本、 建筑、 人脸等多种目标图像, 涵盖了低照度、 高复杂性等多种特征, 可直观检验算法的泛化性与实际应用能力.
2.2 模型训练
本文程序使用Tensorflow1.13[25]框架, 采用Python语言进行构建, 在Ubuntu系统的计算机平台上使用Nvidia1080Ti显卡进行实验. 实验采用数据集GoPro进行网络训练, 在训练过程中图片会被裁切为256×256大小的图像输入网络, 训练批尺寸设定为16, 采用Adam优化器, 损失函数超参数设定为0.04, 网络经过2 000次迭代训练收敛, 得到模型的基本数据.
2.3 实验结果及分析
为检验程序的可靠性与实用性, 本文采用在图像质量评价中广泛使用的量化评价指标, 将去模糊后的图像与原始真实图像进行峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性的比较, 对比网络为近年深度学习领域应用广泛的经典算法, 两个数据集的对比结果列于表1.

表1 数据集测试结果
由表1可见, 在数据集GoPro上进行定量分析, 本文方法较文献[16]方法在PSNR和SSIM上分别提升了0.72 dB和0.001 7, 在数据集Kohler上进行定量分析, PSNR与SSIM则分别提升了0.03 dB和0.000 4. 与文献[11]方法进行比较, 在数据集GoPro上也有一定程度的提升. 而与其他的经典深度学习算法相比, 如采用了三层网络的文献[10]方法, 本文方法具有更大的提升.
在具体图像的定性直观分析上, 本文选用在指标测试中综合表现更好的循环神经(SRN)网络, 对比数据来源为GoPro测试集中的1 111张图像. 图5列举了5张例图及放大细节, 其中每列从左至右分别为模糊图像、 SRN去模糊图像、 本文方法去模糊图像和清晰图像, 同时, 本文也对在数据集Kohle上测试的图像进行了细节对比, 结果如图6所示. 由图5和图6可见, 与SRN算法相比, 本文方法在复原图像上的特征轮廓更准确和清晰, 光影和亮度方面与真实图像相比更贴近, SRN算法在数据集Kohle的部分复原图像在平滑的背景上出现了细微的伪影, 本文方法则较少出现.

图5 数据集GoPro上的复原图像细节Fig.5 Details of restored images on GoPro dataset

图6 数据集Kohler上的复原图像细节对比Fig.6 Detail comparison of restored images on Kohler dataset
本文在数据集Lai上对真实图像进行了视觉对比, 对比算法为SRN网络与文献[16]网络. 如图7所示, 本文选用具有代表性的3类图像: 人脸、 文字与低光图像. 由图7可见: 在人脸图像中, 本文方法具有较好的整体观感, 脸部色彩纹理平滑, 伪影较少, 但在人脸边界的处理中表现较差, 出现了模糊现象; 在文字方面, 本文方法具有较明显的背景-前景对比度, 清晰度与SRN等方法相似; 在低光环境中, 本文方法表现较好, 相比SRN网络和文献[16]网络, 具有更高的字母识别度. 因此, 在真实图像上本文方法在轮廓边缘等细节与SRN方法相比较差, 但在低光图像与色彩对比度上具有好的去模糊效果, 且图像整体纹理平滑, 观感较好.
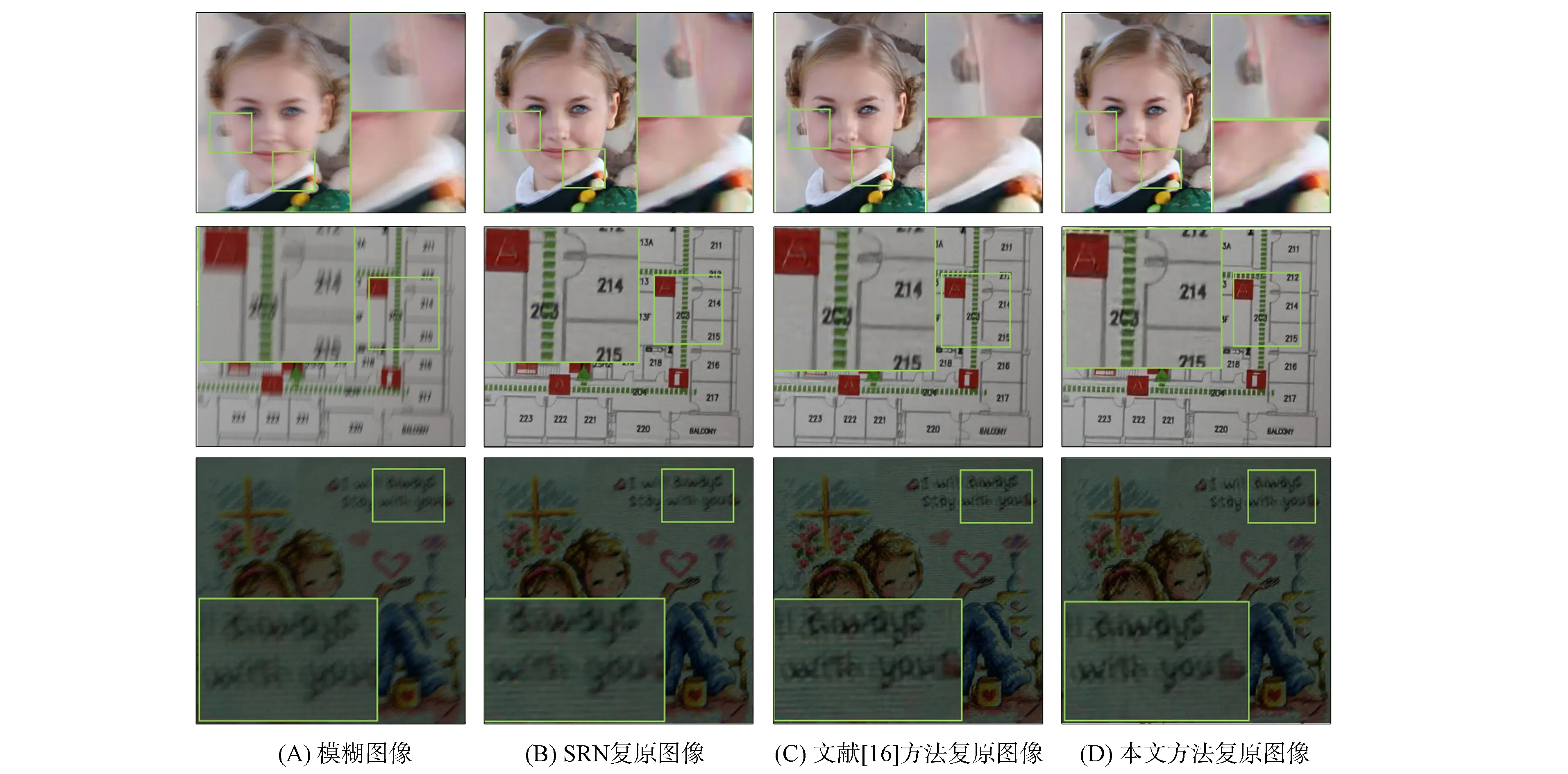
图7 数据集Lai上的复原图像细节对比Fig.7 Detail comparison of restored images on Lai dataset
综上所述, 针对复杂的单图像盲去模糊问题, 本文以现有方法为基础, 提出了一种基于循环多尺度的盲去模糊网络. 为使网络能充分利用有效特征, 设计了残差通道选择模块并将其融入到循环网络框架中, 进行通道的选择优化. 同时在框架中设计了跨卷积层的跳跃连接, 以保留原始图像的有用特征. 此外, 设计了用于图像盲去模糊的多尺度结构损失函数, 通过综合优化图像的像素级差异和大尺度上的结构、 亮度、 对比度获得最佳的去模糊视觉效果. 实验结果表明, 本文方法可在多个数据集上获得较优的图像盲去模糊效果, 与文献[16]方法相比, 在数据集GoPro上PSNR与SSIM分别提升了0.72 dB和0.001 7, 在数据集Kohler上PSNR与SSIM分别提升了0.03 dB和0.000 4, 较其他对比方法也有不同程度的提升, 整体表现优于经典深度学习去模糊算法, 在多个数据集中具有较好的稳定性.

