基于k多数值代表的混合矩阵对象数据聚类

赵 健

(长治学院 计算机系, 山西 长治 046011)

数据的多样性与复杂性导致每个记录都是一个特征向量, 每个对象都由多个特征向量组成, 每个对象称为矩阵对象, 这类数据广泛应用于银行、 保险、 电信、 零售、 医学等领域[1-2]. 在大多数情况下, 矩阵对象由分类属性和数字属性共同描述, 而用户行为的变化是一个随时间变化的动态演化过程, 因此如何实现有效矩阵对象数据聚类成为研究的热点[3].

用传统聚类算法解决上述问题, 需对矩阵对象数据进行变换, 主要有两种方法： 一种是将矩阵对象压缩成一个向量, 常用的压缩方法是分别用分类属性和数值属性的模式和方法表示矩阵对象. 文献[4]为克服不同初始类中心对聚类结果的影响, 针对分类型矩阵数据, 提出了一种新的初始聚类中心选择算法； 文献[5]提出了三类广义多实例假设, 并在基于广义假设条件下建立了一个层次结构； 文献[6]提出了一种基于簇间信息的分类矩阵对象数据的聚类算法, 该算法利用k-modes算法实现矩阵对象聚类. 但上述方法使数据大部分信息丢失, 并且只考虑平均值, 不能反映具体的数据信息.

另一种方法是将每个属性值视为一个新的属性进行处理. 文献[7]通过给出一种矩阵对象自身的内聚度和该矩阵对象与其他矩阵对象之间的耦合度, 定义矩阵对象的孤立因子, 提出了一种基于信息熵的孤立点检测算法; 文献[8]基于信息熵定义了一种属性权重的新度量方法, 并提出一种加权k-prototype算法实现矩阵对象数据聚类; 文献[9]提出了一种基于密度峰值思想的加权犹豫模糊矩阵对象数据聚类算法, 该算法不仅降低了簇中心计算的复杂度, 而且提高了对不同规模以及任意形状矩阵对象数据集的适应性. 但上述方法会使矩阵对象数据更稀疏和高维, 从而极大降低了聚类准确性.

为解决传统聚类方法存在的局限性, 本文提出一种基于k多数值代表的混合矩阵对象数据聚类方法. 通过定义一种新的相异度度量计算两个数值矩阵对象之间的差异, 提出k多数值代表聚类算法实现混合矩阵对象数据的聚类. 实验结果证明了本文方法的有效性.

1 矩阵对象数据的聚合

1.1 问题描述

设X={X1,X2,…,Xn}表示由m属性{A1,A2,…,Am}描述的矩阵对象数据集, 其中Xi(1≤i≤n)表示第i个带有ri个特征向量的矩阵对象, 表示为

(1)

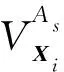
1.2 算法设计

1.2.1 两个数值矩阵对象间的相异度

本文将每个矩阵对象作为一个ri_by_m(ri≥1)型矩阵, 且矩阵对象不同, 其ri值也不同.由于由两个特征向量与两个矩阵对象间的欧氏距离测得的相异度不符合所有特征向量与矩阵对象观测分类有关的特征, 所以本文提出一种测量数值矩阵对象相异度的新方法.已知每个距离需在相同特征空间内测量, 假设属性特征独立, 两个矩阵对象间的差异度可通过其特征的差别测得.由于可以将任意矩阵对象视作m型ri维向量, 因此上述问题可转化为测量相同特征空间内两个长度不等的向量之间差异度问题.由于数值属性值具有连续性, 因此上述方法可借助其相邻值进行测量计算.

定义1[5]假设X为一已知的数值矩阵对象数据集,Vs为X在属性As内的域值集.Xis=(vi1s,vi2s,…,viris)T表示Xi(Xi∈X)的第s个ri维列向量,εs为已知参数, 且∀v∈Vs, 上述列向量的相邻值在Xis内的数量可表示为

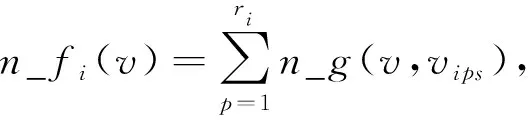
(2)

其中

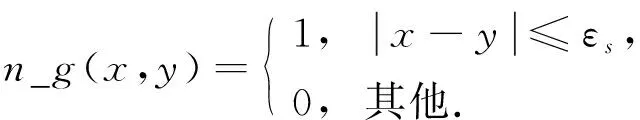
(3)

定义2[6]已知由m属性{A1,A2,…,Am}定义的数值矩阵对象Xi和Xj, 则Xi和Xj间的相异度度量可表示为

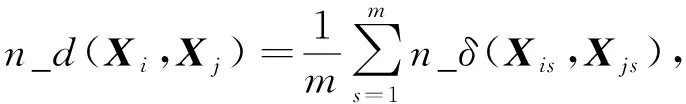
(4)

其中

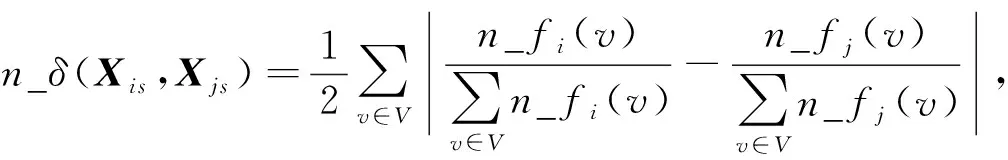
(5)

V=Xis∪Xjs, |·|表示绝对值, 并且需加入归一化因子0.5, 使得0≤n_δ(Xis,Xjs)≤1, 当且仅当Xis∩Xjs=Ø时,n_δ(Xis,Xjs)=1.

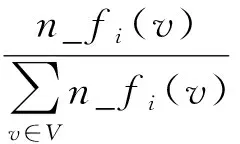
1.2.2 启发式聚类中心更新方法

定义3已知由m属性描述的数值矩阵对象数据集X={X1,X2,…,Xn}.设Vs为X在属性As内的值域集, ∀v∈Vs, 其权重表示为

(6)

已知矩阵对象Xi(Xi∈X), 由式(2)可知,n_fi(v)为属性值v在Xis内相邻值的个数,n_fi(v)/ri为属性值v在Xis内的重要程度.n_fi(v)越高, 表示v在Xis中越重要.被选中的代表聚类中心属性值应在任一矩阵对象中都较重要.在式(6)中, 有0≤n_fi(v)/ri≤1, 且0≤n_ω(v)≤1.当且仅当n_fi(v)/ri=1(∀i∈{1,2,…,n})时, 有n_ω(v)=1.即当且仅当属性值在任一矩阵对象中很重要时, 该属性值的权重较高.

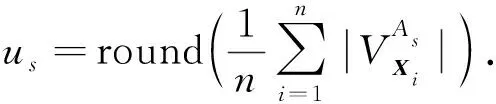
算法1启发式聚类中心更新算法.

输入：m属性描述的n数值矩阵对象集X, 用于计算相邻值的参数集ε={ε1,ε2,…,εm}；

输出：X的一个聚类中心Q；

步骤1) fors=1∶1∶mdo

步骤2) sum=0,Q=Ø；

步骤3) fori=1∶1∶ndo

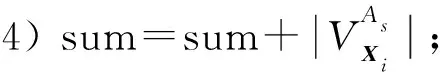
步骤5) end for

步骤6)us=round(sum/n);

步骤7) fort=1∶1∶|Vs| do

步骤9) end for

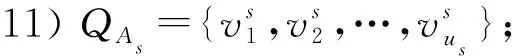
步骤12)Q=Q∪QAs；

步骤13) end for

步骤14) 返回Q.

1.2.3k-Mnv-Rep算法

已知公式聚类k(≪n)内的数值矩阵对象集X={X1,X2,…,Xn}, 使用k-Mnv-Rep算法对下列目标函数最小化：

(7)

其中W=(ωli)为k_by_n{0,1}矩阵, 当ωli=1时, 将目标Xi分配入聚类l；Q={Q1,Q2,…,Qk},Ql∈Q表示聚类l中的多数值表示.

对目标函数的最小化为NP难问题, 一般情况下, 可通过不断迭代直到完成聚合, 从而解决两个子问题, 进一步解决F(W,Q)问题: 1) 在迭代t中, 始终令Q=Qt, 利用式(3), 解决F(W,Qt)减小问题, 并找出F(W,Qt)取得最小值时的Wt; 2) 通过运行算法1, 用上述得到的Wt值解决F(Wt,Q)减小问题, 并找出F(Wt,Q)取得最小值时的Qt+1.

算法2k-Mnv-Rep算法.

输入：m属性描述的n数值矩阵对象集X, 需聚合的聚类个数k, 阈值o;

输出： 聚合后所有目标的标签cid;

步骤1) 生成随机数k, 通过指数取得初始中心k；

步骤2) 设Q={Ql,Q2,…,Qk}为初始中心, 且value=0, num=0;

步骤3) while num≤100 do

步骤4) value1=0;

步骤5) fori=1∶1∶ndo

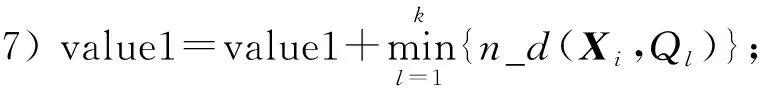
步骤8) end for

步骤9) if |value1-value|≤o, break； else value=value1, 且num=num+1；

步骤10) forl=1∶1∶kdo

步骤11) 运行算法1, 更新聚类中心Ql；

步骤12) end for

步骤13) end while.

对k-Mnv-Rep算法计算复杂性的分析如下.

1) 计算相异度： 属性As内两个数值矩阵对象间相异度的复杂性可表示为O(|Vs|), 属性m内两个数值矩阵对象间相异度的计算复杂性可表示为O(m|V′|), 其中|V′|=max{|Vs|, 1≤s≤m}.

2) 更新聚类中心： 属性As属性值权重的计算复杂性可表示为O(n|Vs|), 属性m内k型聚类中心的计算复杂性可表示为O(kmn|V′|), 其中|V′|=max{|Vs|, 1≤s≤m}.

3) 通过t型迭代进行聚合时,k-Mnv-Rep算法的总计算复杂性可表示为O(tmnk|V′|), 其中|V′|=max{|Vs|, 1≤s≤m}.因此, 该算法的时间复杂性与矩阵对象数量、 属性数量、 聚类数量和属性值数量呈线性正相关.

1.3 用于处理混合矩阵对象数据的算法

1.3.1 两个混合矩阵对象间的相异度

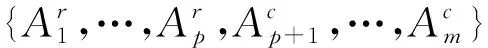
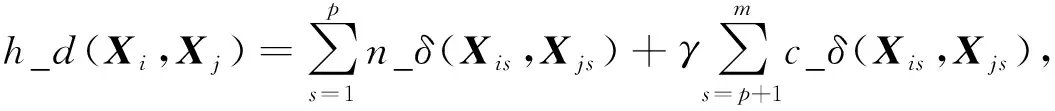
(8)

其中γ为权重, 可使两种数据得到相同处理.As内范畴型矩阵对象的距离可表示为

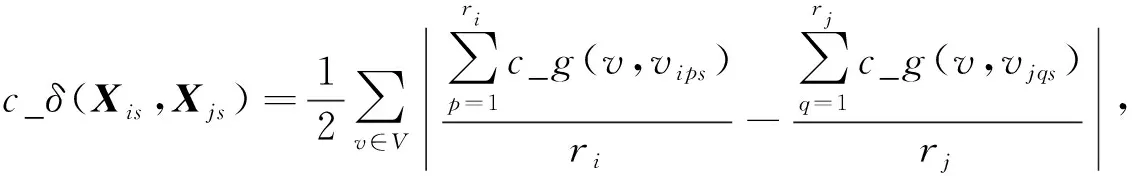
(9)

其中V=Xis∪Xjs, 当两个参数相等时,c_g(·,·)=1, 其余情况下,c_g(·,·)=0.需加入归一化因子0.5, 使得0≤c_δ(Xis,Xjs)≤1.当且仅当Xis∩Xjs=Ø时,c_δ(Xis,Xjs)=1.

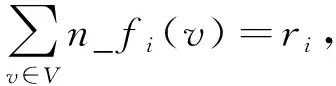
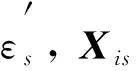
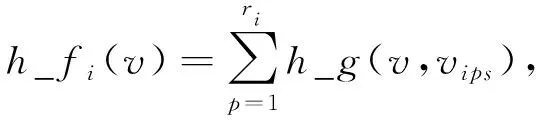
(10)

其中

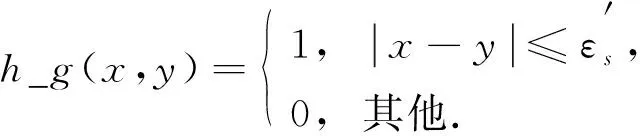
(11)

定义6设X为由属性m描述的混合矩阵对象数据集.∀Xi,Xj∈X,Xi和Xj间的相异度可表示为

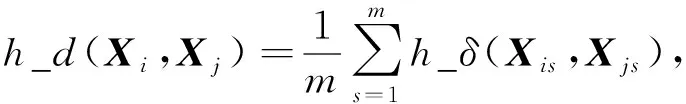
(12)

其中

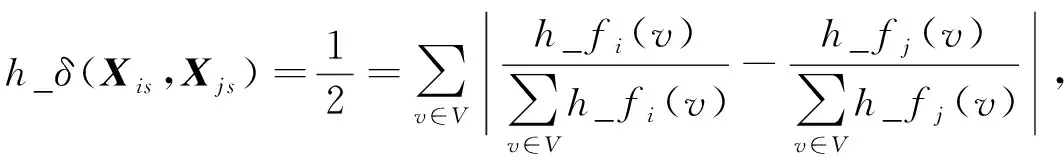
(13)

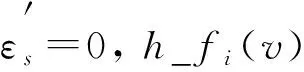
1.3.2 属性值的权重更新方法

分别通过数值属性和范畴属性更新聚类中心.在任一属性中, 更新方法应以较高权重得到若干数值.权重的定义是更新算法的关键.根据式(10)可知, 当v值已知时, 公式在数值属性和范畴属性内一致.因此, 在已知混合数据集内, 属性值的权重可定义如下.

定义7设X为属性m描述的含有n个混合矩阵对象的数据集,Vs为X在属性As内的域值集, ∀v∈Vs, 其权重定义为

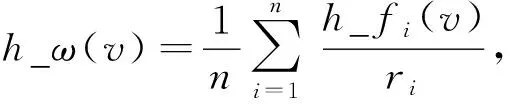
(14)

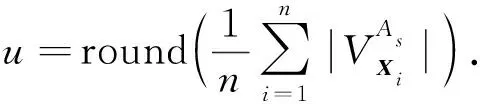
1.3.3k-Mv-Rep算法

设X={X1,X2,…,Xn}为混合矩阵对象数据集.k-Mv-Rep算法可以将X聚合入k(≤n)聚类内, 从而实现下列目标函数的最小化：

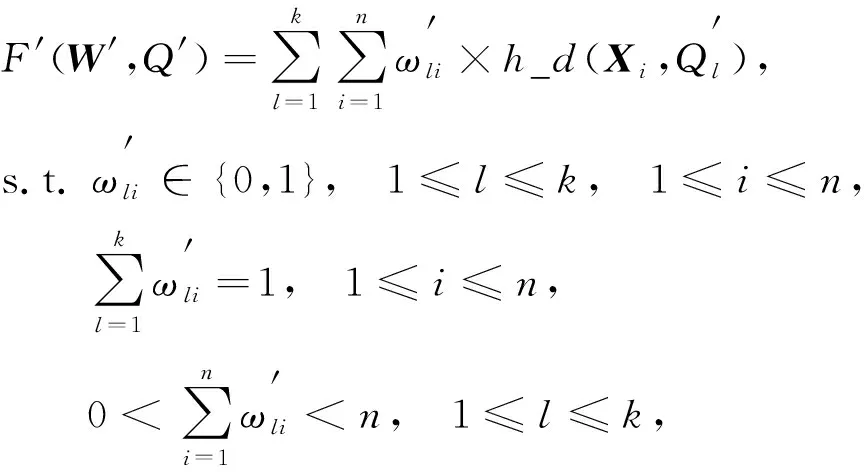
(15)

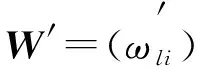
与k-Mnv-Rep算法相似, 通过使用一种新的启发式聚类中心更新方法处理混合矩阵对象数据取得F′(W′,Q′)的局部最小值, 取得局部最小的过程与k-Mnv-Rep算法相同.

算法3k-Mv-Rep算法.

输入： 属性m描述的n混合矩阵对象数据集X, 需聚合的聚类个数k, 域值o；

输出： 聚合后所有目标的标签cid；

步骤1) 生成k个随机数, 通过指数取得k个初始中心；

步骤2) 设Q={Q1,Q2,…,Qk}为初始中心, 且value=0, num=0；

步骤3) while num≤100 do

步骤4) value1=0;

步骤5) fori=i∶1∶ndo

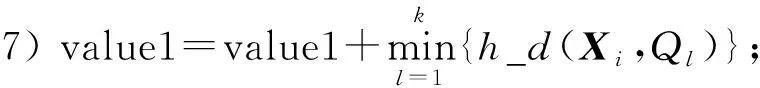
步骤8) end for

步骤9) if |value1-value|≤o, break； else, value=value1且num=num+1；

步骤10) forl∶1∶kdo

步骤11) 利用式(14)更新聚类中心Ql；

步骤12) end for

步骤13) end while.

k-Mnv-Rep算法的总计算复杂性可表示为O(tmnk|V′|), 这里t表示迭代, 且|V′|=max{|Vs|, 1≤s≤m}. 因此, 该算法的计算时间复杂性与矩阵对象数量、 属性数量、 聚类数量和属性值数量呈线性正相关.

2 实验与分析

2.1 评估指标

采用5个外部指标评估上述两种算法, 分别为精确度(AC)、 准确度(PE)、 召回率(RE)、 调整兰德系数(ARI)和归一化互信息(NMI)[10].

设X为一矩阵对象数据集,C={C1,C2,…,Ck′}为X的聚合结果,P={P1,P2,…,Pk}为X的实分区.nij为Pi和Cj中相同的矩阵对象数量, 即nij=|Pi∩Cj|,pi和cj分别为Pi和Cj中的矩阵对象数量.5个评估指标分别定义如下：

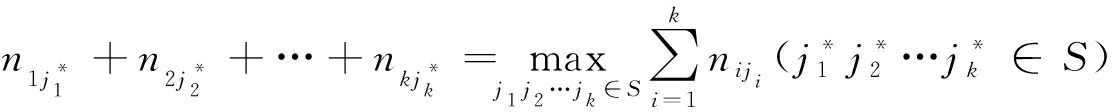
2.2 数值矩阵对象数据实验

2.2.1 真实数据集

由于缺少公开数值矩阵对象, 因此本文实验使用多示例数据集评估k-Mnv-Rep算法, 另一部分实验围绕9组真实数据集展开, 数据集信息列于表1.

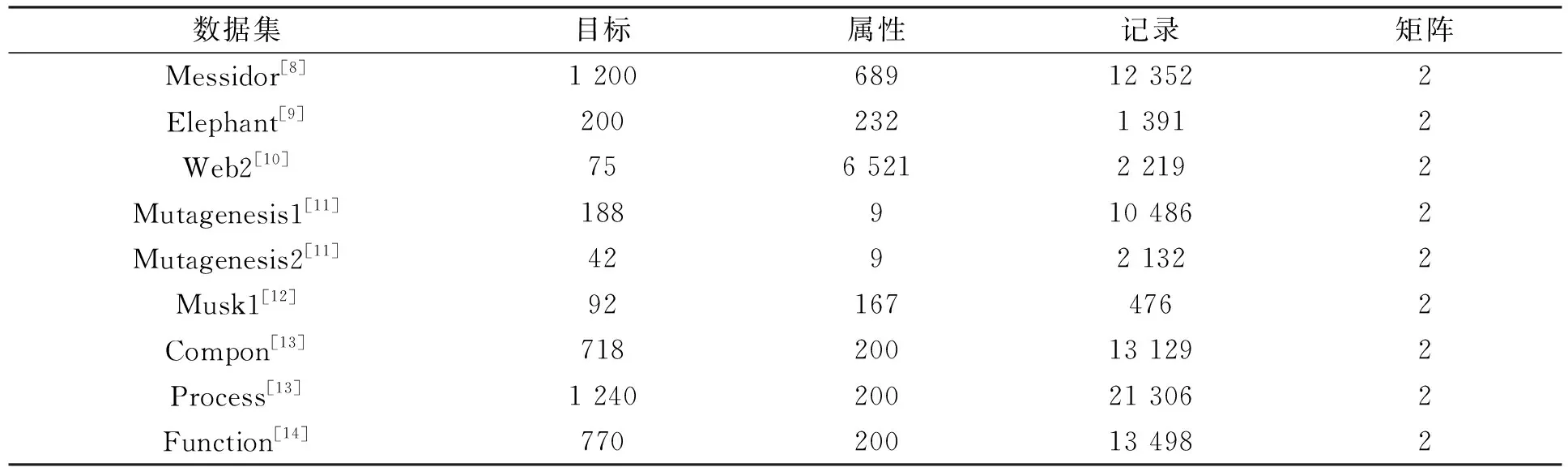
表1 数据集信息

2.2.2 比较结果

通过表1中9种数值型数据集实验, 将k-Mnv-Rep算法与使用3种距离表示方式的包级多实例聚类算法(BAMIC)[11]、 自适应邻域聚类算法(CAN)[12]、 表示自适应邻域聚类算法(PCAN)[13]、L1范数垃圾回收算法(CLR-L1)[14]、L2范数垃圾回收算法(CLR-L2)[15]得出的结果进行比较. 上述后4种算法的输入数据集中, 每个矩阵对象都由一个向量描述. 因此, 以每个矩阵对象的中值作为每个属性的属性值.

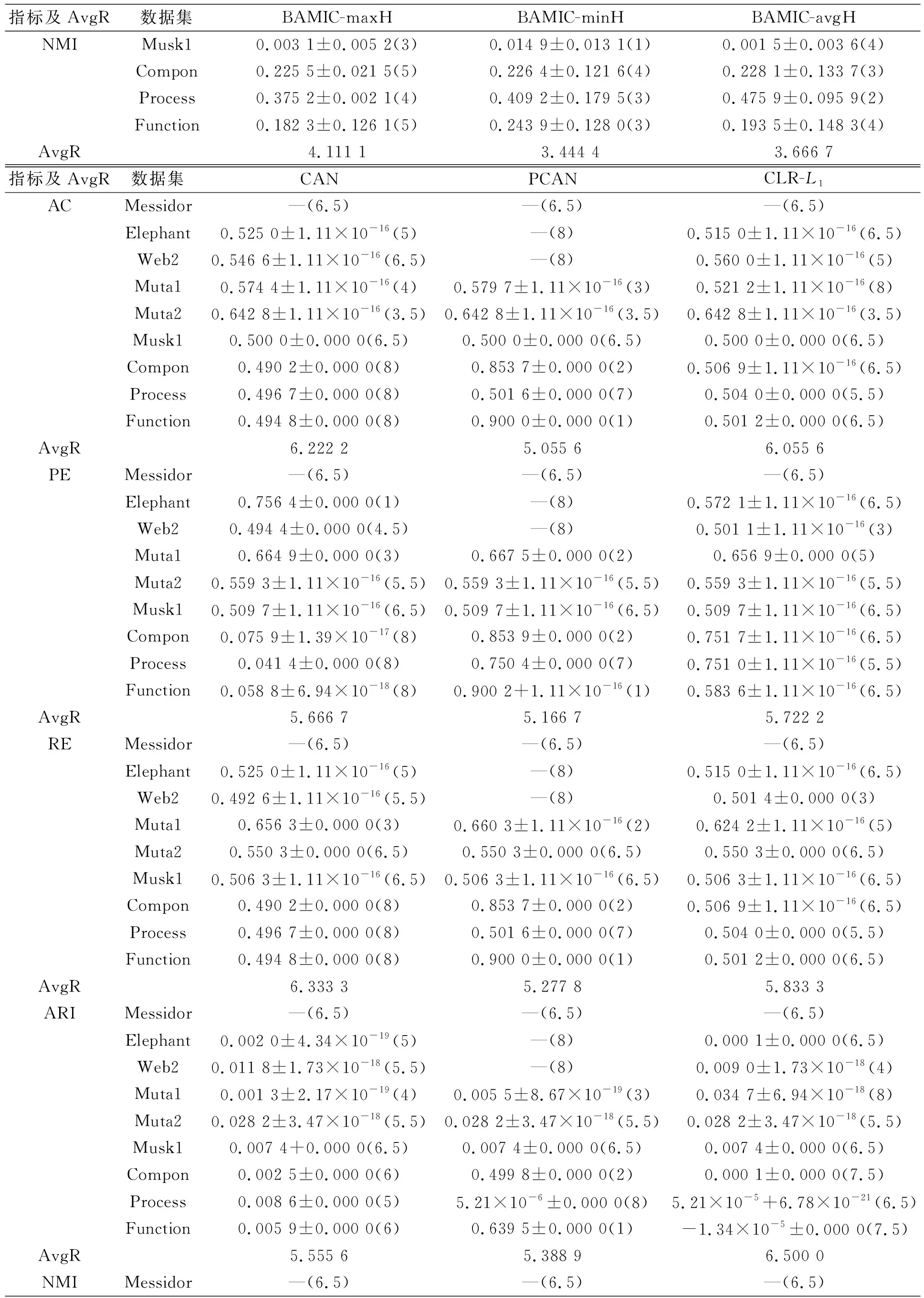
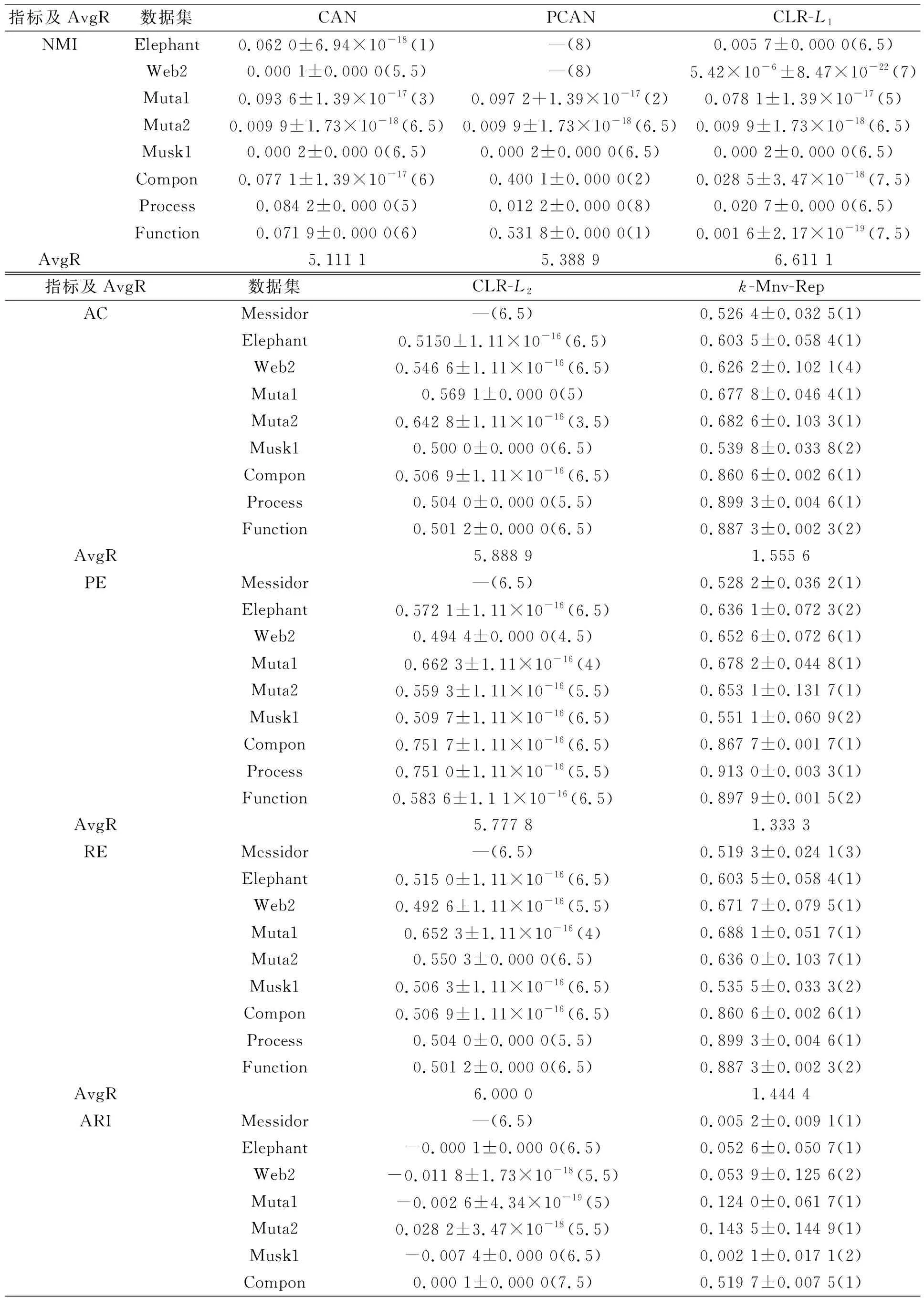
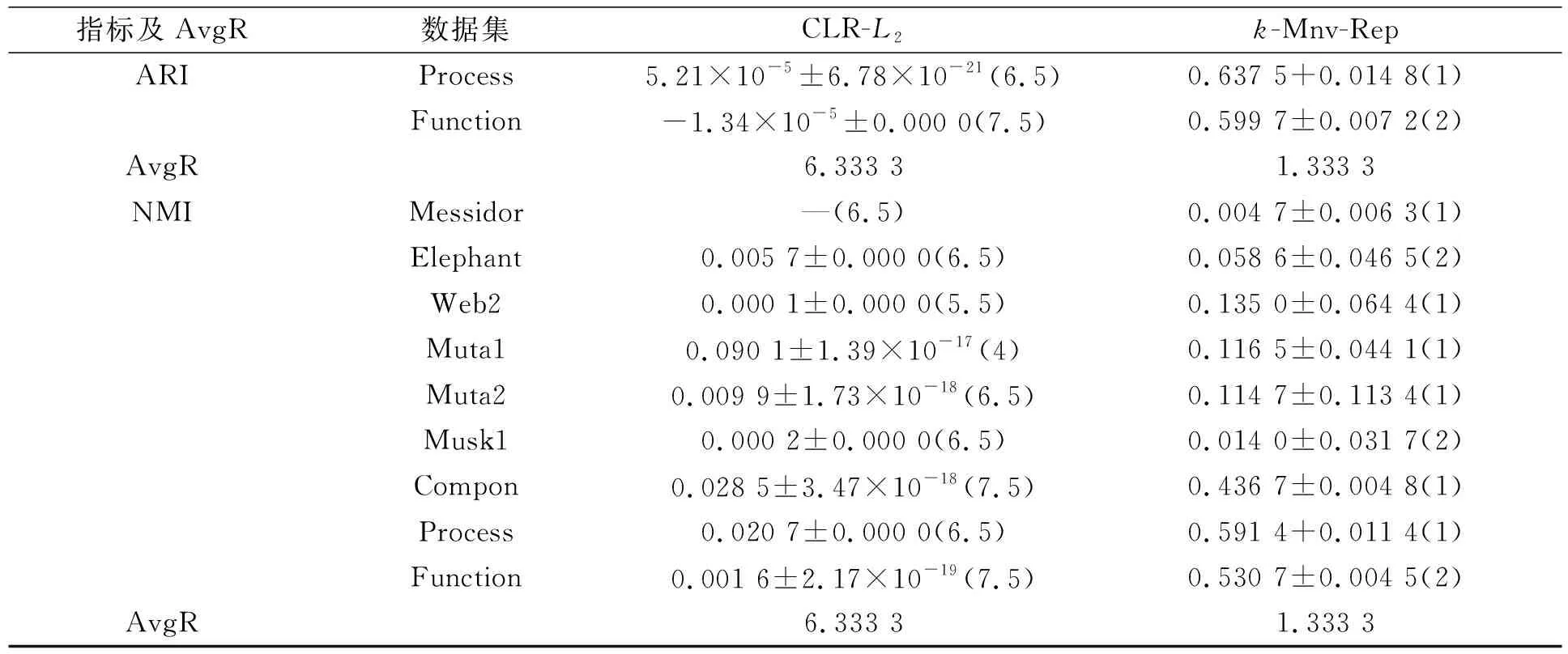
在实验过程中, 将8种算法各运行30次, 取最终结果的中值. 设参数εs大小为第s属性内X标准差的1/2, 在k-Mnv-Rep算法中, 设该参数为0.2. 不同算法9个数据集的对比结果列于表2, 其中符号“±”左侧为中值, 右侧为标准差. 在每个数据集中, 对评估指数值进行排序, 最高值排序为1, 次高值排序为2, 依此类推, 如表2中括号内所示. AvgR表示所有算法在9个数据集中的平均排序.

由表2可见,k-Mnv-Rep算法的AvgR值在所有评估指数中排序最高, 即k-Mnv-Rep算法在总体上优于上述其他算法. 在8个数据集中,k-Mnv-Rep算法的每个评估指标都优于其他算法； 在数据集Function中, 只有PCAN算法的性能优于k-Mnv-Rep算法, 但由于PCAN算法无法处理逆矩阵, 因此该算法不能处理所有数据聚类. 并且在数据集Messidor,Muta2,Process中, BAMIC-avgH算法优于BAMIC-minH算法和BAMIC-maxH算法的AC值; 在数据集Muta1,Compon中, BAMIC-maxH算法优于BAMIC-minH算法和BAMIC-avgH算法的AC指标; 在数据集Elephant,Web2,Musk1,Function中, BAMIC-minH算法的性能最优. BAMIC算法的其他指标也出现了相同结果. 因此, BAMIC算法很难从3种距离中得出最佳距离.

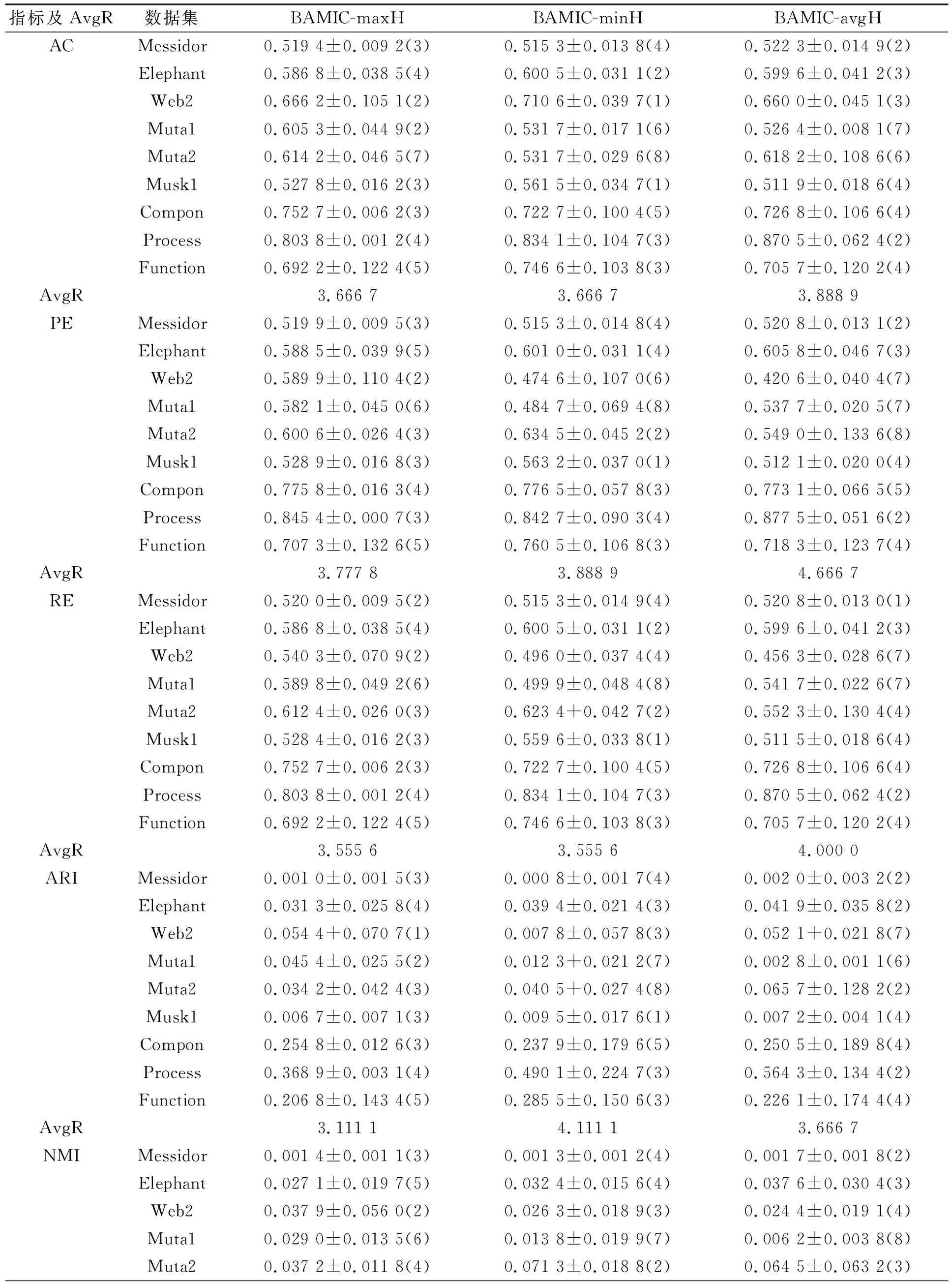
表2 不同算法9个数值型数据集的比较结果

续表2

续表2

续表2

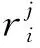
表3 5类实验中上述算法的平均排序值

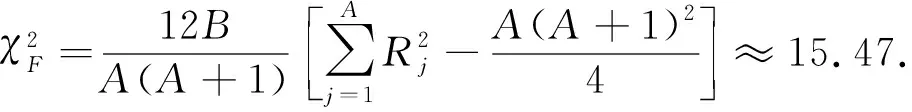
(21)

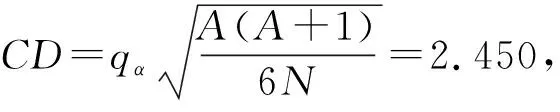
图1为8种算法对5个评估指标进行Bonferroni-Dunn实验的结果, 其中圆圈表示算法的平均排序, 线段表示临界差CD.由图1可见,k-Mnv-Rep算法与CAN,PCAN,CLR-L1,CLR-L2四种算法的所有指标均差异较大, 与BAMIC-minH,BAMIC-maxH,BAMIC-avgH三种算法则差异较小. 而BAMIC-minH,BAMIC-maxH,BAMIC-avgH三种算法的指标几乎无差异, CAN,PCAN,CLR-L1,CLR-L2四种算法的指标几乎无差异. 从平均排序结果可见,k-Mnv-Rep算法性能最佳. 综上, 因为k-Mnv-Rep算法的排序较高、 差异值较大, 所以k-Mnv-Rep算法优于其他对比算法.

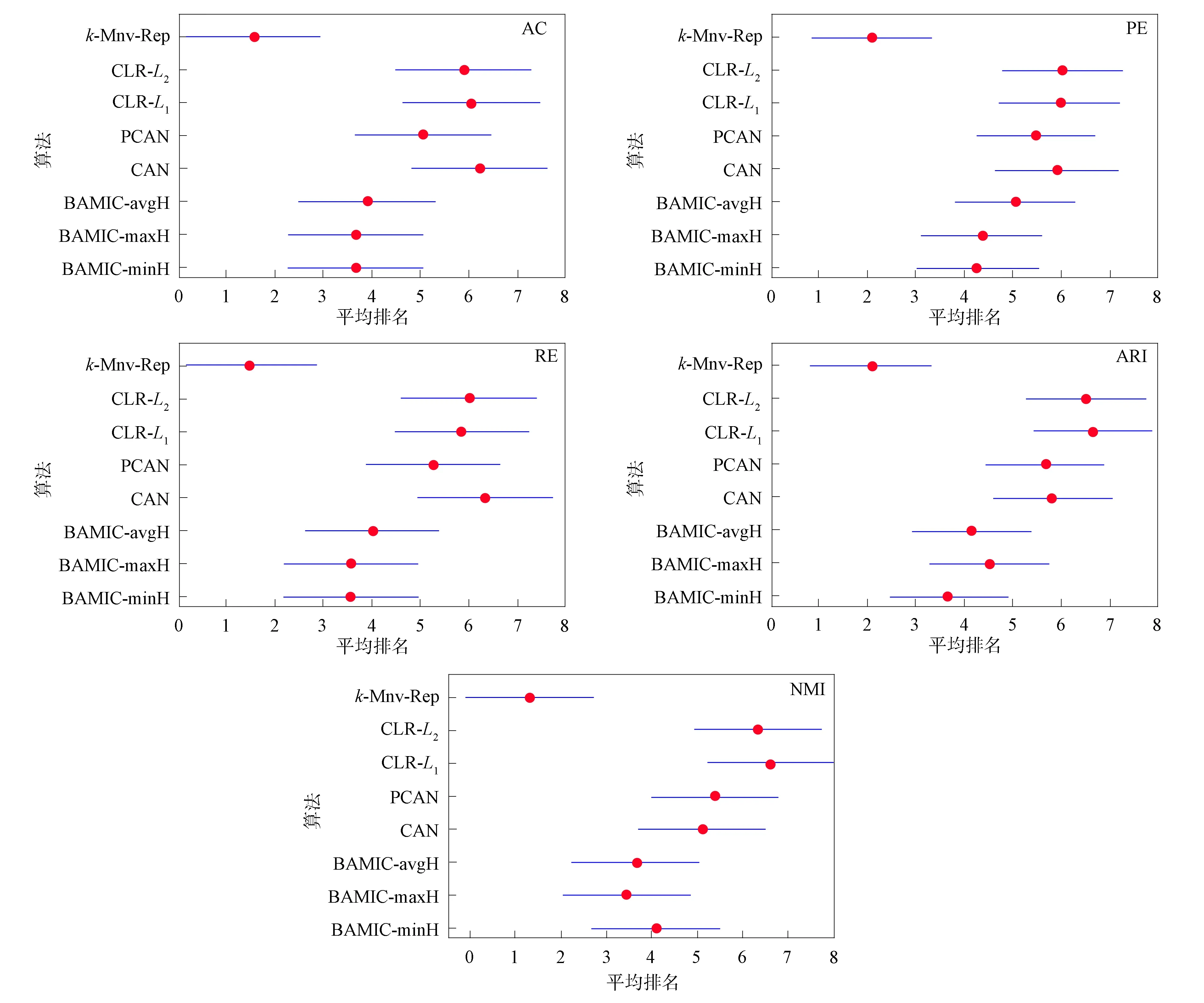
图1 8种算法在Bonferroni-Dunn实验中的5个指标Fig.1 Five indexes of eight algorithms in Bonferroni-Dunn experiment

2.3 混合矩阵对象数据实验

下面进行混合数值矩阵对象实验, 评估k-Mv-Rep算法的有效性. 已知有真实混合矩阵对象数据集, 并已知k-Mv-Rep算法和k型算法的比较结果.

2.3.1 真实混合数据集

由于缺少公开混合矩阵对象, 因此本文实验中使用真实混合数据集评估k-Mnv-Rep算法的有效性. 为评估上述算法, 应对上述数据集进行结构预处理. 本文用多维尺度法对数据进行可视化处理. 由式(12)可得出n_by_n型距离矩阵, 用多维尺度法主要是为了将该矩阵转移到MATLAB生成的mdscale方程中, 从而获得P维度中n个点的构型.n点间的欧氏距离与n_by_n型距离矩阵中相应相异点的单调变换大致相同, 因此, 可通过将n点可视化显示数据的分布情况.设P=2, 对数据进行可视化.在大多数实验案例中, 真实数据集的分布通常是无序的.利用可视化, 可通过删除部分点获得相对清晰的数据结构.

首先从数据集Author中选出相应系统内符合范围x<0.55且y>0.16或x<0.55且y<-0.16的目标, 进行可视化后成为一个新数据集, 然后对如图2所示的新数据集进行可视化. 利用可视化可推断出聚类的数量和每个矩阵对象的标签信息, 数据集Author信息列于表4.

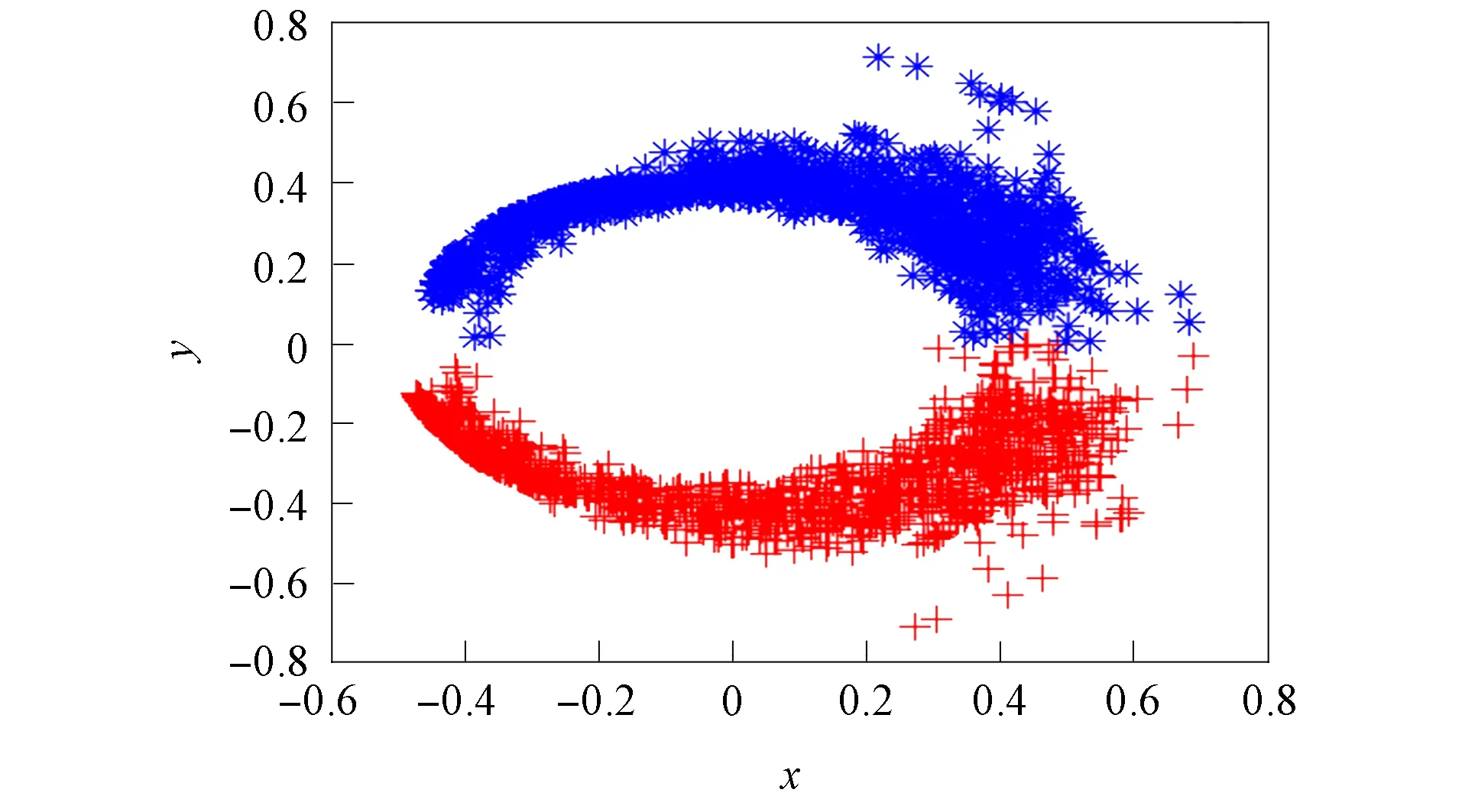
图2 数据集Author的分布Fig.2 Distribution of data set Author

表4 数据集Author信息

2.3.2 对比结果分析

已知部分聚类算法无法直接处理混合矩阵目标, 所以应在该子部分内应用k型算法. 由于矩阵对象本质上是矩阵而非向量, 因此需要将矩阵对象转换为能使用k型算法的形式. 混合矩阵对象范畴属性的属性值由模式表示, 数值属性的属性值由中值表示. 这样即可将混合矩阵对象变形为向量, 从而可以使用k型算法处理矩阵对象数据集.

分别运行k型算法和k-Mv-Rep算法50次, 取实验结果的中值作为最终结果. 设k-Mv-Rep算法的参数ε=0.2,k型算法γ的参数值为文献[16]中所有数值属性的标准差, 表5列出了数据集Author中k型算法和k-Mv-Rep两种算法的比较结果. 由表5可见,k-Mv-Rep算法的5个评估指标值均优于k型算法, 并且k-Mv-Rep算法比k型算法的精确度约高13%. 因此,k-Mv-Rep算法优于k型算法.

表5 两种算法在数据集Author中的实验结果对比

2.4 参数ε对算法的影响

k型算法和k-Mv-Rep算法的参数ε已知, 并作为终止程序的控制条件. 当目标方程的变换小于ε时, 程序终止. 因此, 不同参数大小可能会产生不同的聚类结果, 如何确定该参数十分重要. 分别在相应数据集内按照不同公式运行k型算法和k-Mv-Rep算法各30次, 公式大小变化以0.05为梯度, 由0.05增加至0.35, 并记录AC的中值和迭代次数, 结果分别如图3和图4所示.

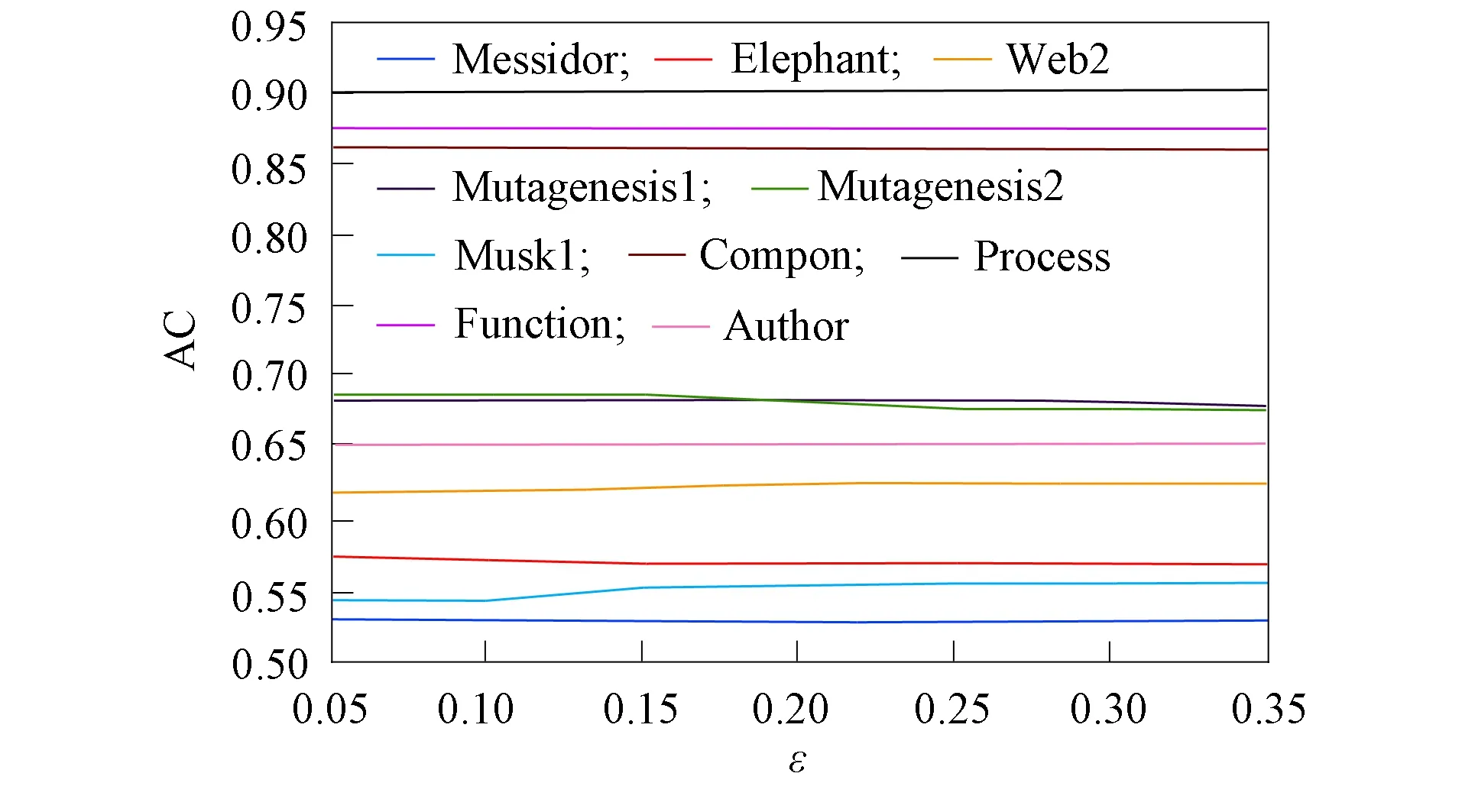
图3 不同ε在10个数据集内的准确率Fig.3 Accuracy of differnt ε in ten data sets

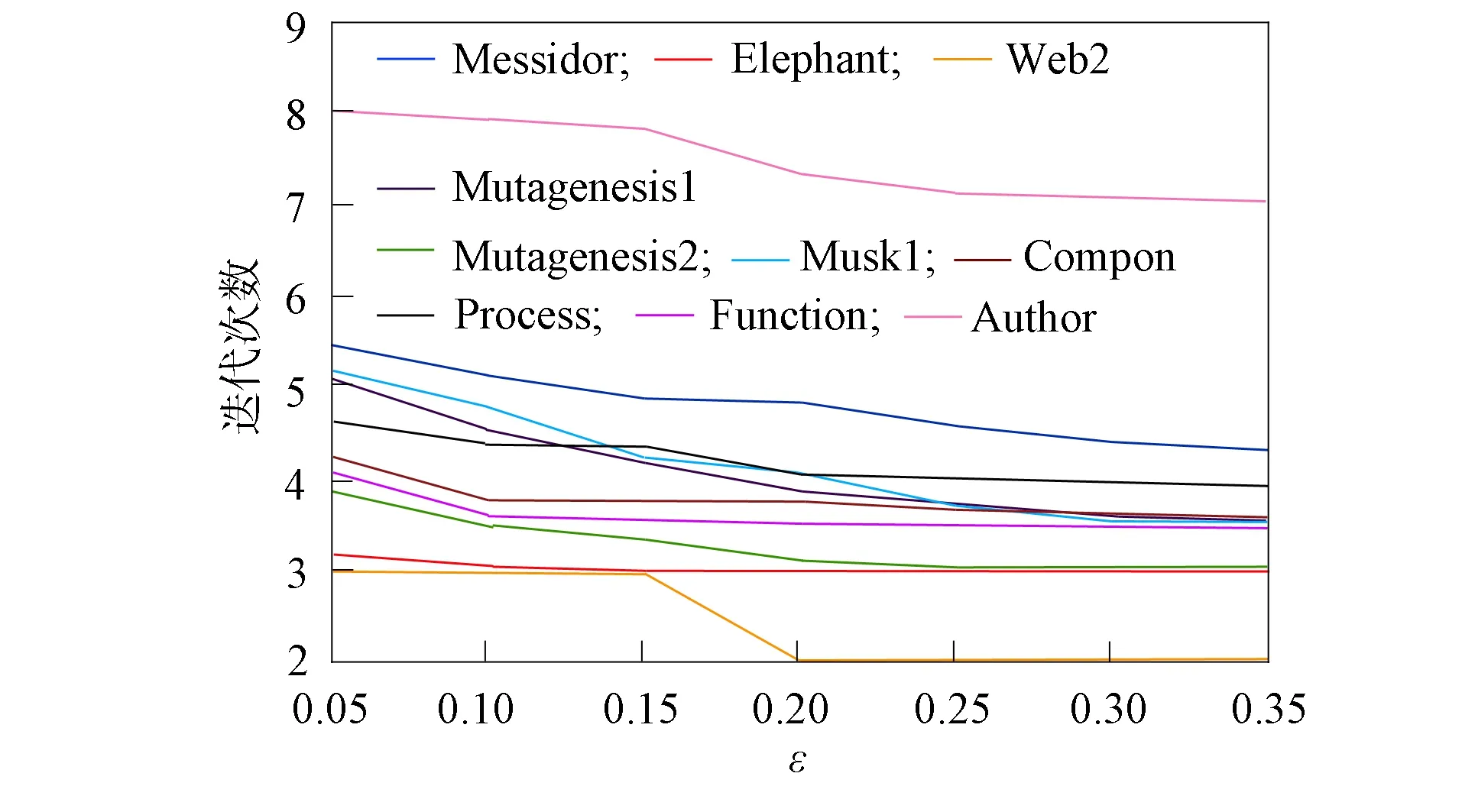
图4 不同ε在10个数据集内的迭代次数Fig.4 Iterations of differnt ε in ten data sets

由图3可见, 随着ε增大, AC在10个数据集内均有轻微浮动, 但总体稳定. 由图4可见, 随着ε增大, 迭代次数在10个数据集内呈总体下降趋势, 一般当ε>0.2时, 迭代次数下降趋势较缓. 在上述两种算法中, 综合AC结果和迭代结果, 令ε=0.2.

2.5 聚合性检验

因为本文提出的用于更新聚类中心的k-Mv-Rep算法和k-Mnv-Rep算法均属于启发式算法, 所以要对这两种算法进行聚合性检验, 以保证其合理性. 在所有实验中, 记录目标方程值和所有迭代次数. 图5为目标方程值变化与k-Mv-Rep算法迭代的比值. 由图5可见, 随着迭代次数增加, 目标方程值呈下降趋势. 在10个数据集内的聚合性检验结果也同样证明了该结论.

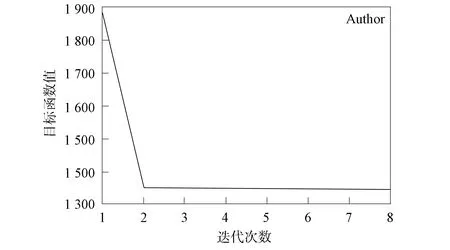
图5 目标方程值变化与k-Mv-Rep算法迭代的比值Fig.5 Ratio of value change of objective equation to iteration of k-Mv-Rep algorithm

综上所述, 为解决数据的稀疏性和高维问题, 并有效反映聚类中心与聚类内矩阵对象的分布, 本文提出了一种基于k多数值表示的混合矩阵对象数据聚类方法. 由真实数据集与合成数据集的实验结果可得如下结论：

1) 本文聚类算法对于稀疏数据集和高维数据集均能保证良好的聚类效果, 证明该方法能解决数据集的稀疏和高维问题；

2) 本文算法对于不同的数据集均实现了精度较高的聚类, 证明该算法的泛化能力较强, 能有效反映聚类中心与聚类内矩阵对象的分布；

3) 本文算法的聚类准确度对于参数具有良好的鲁棒性, 并且聚合性检验证明了算法的合理性.