环形电机耦合网络混沌行为的抑制控制

梅春草, 许丽娟

(广州华商学院 数据科学学院, 广州 511300)

永磁同步电动机(PMSM)具有效率高、 转矩电流比和功率密度大等优点[1-2], 作为一种可从模型上证明的混沌电机系统, 其混沌行为的控制与同步研究已引起人们广泛关注. PMSM系统的参数值在一定范围内会出现混沌行为,d-q轴电流直接影响转矩控制, 为实现更好的系统动态性能, 其在矢量控制的PMSM中发挥重要作用[3]. Wei等[4-5]研究了PMSM系统的混沌和分岔等动力学行为, 结果表明, PMSM达到混沌控制的表现为当时间趋于无穷时, 永磁同步电动机的状态变量达到稳定平衡状态. 为消除PMSM的混沌行为, 人们提出了较多控制策略, 其中包含线性控制器和非线性控制器. 由于PMSM是一个受参数变化和多重耦合状态影响的非线性系统, 采用线性控制算法不易获得良好的控制性能, 因此对非线性反馈控制器的设计越来越多, 如模糊逻辑控制[6]、 滑模控制[7]、 预测控制[8]、 神经网络控制[9]和自适应控制[10]等. PMSM作为一个三维自治系统可结合非线性定理推出合适的控制函数, 如基于有限时间稳定理论、 Lyapunov稳定性理论以及LaSalle不变集定理设计的控制算法[11-13]均具有结构简单、 控制效果好以及控制时间短等优点.

PMSM在电力系统中作为负载具有耗电功能, 控制电机速度的稳定性在电力系统输电-发电-配电过程中有重要影响. Tan等[14]采用直流电机等效分数阶模型对永磁同步电机速度伺服系统进行建模, 利用自适应递推最小二乘约束广义预测控制器(GPC)控制了模型阶数未知、 恒负载转矩和正弦负载两种负载状态下永磁同步电机的转速问题. 在电网稳定运行过程中, 突然加入负载对电网互联是不可避免的, 研究并网后电力系统的同步稳定性具有一定的实际意义[15-16]. 文献[17]通过计算电力系统中负载与发电机相互连接的相关系数, 实现了电网的自然同步； 文献[18]以永磁同步电动机外部耦合Kuramoto电网模型为例, 研究了空间分布式电网与用户负载间的同步问题； 在网络拓扑关系中, 双向耦合的小世界电机网络基于动力中继节点的参数不匹配降低了同步耦合强度的临界值, 以促进节点间的同步特性[19]. 目前研究的网络拓扑结构主要有Erdös-Rényi(ER)随机网络模型[20]、 环形网络模型[15]和Barabsi-Albert(BA)无标度网络模型[21]等, 因此利用网络拓扑结构的宏观规律对电机网络进行同步控制, 可进一步探索电机网络的同步聚散能力与网络拓扑结构的内在关系.

基于此, 本文基于Lyapunov稳定性理论提出一种新的非线性反馈控制器, 研究具有反馈控制器的单台PMSM混沌行为, 并将这台PMSM作为外部驱动系统, 加入环形电机网络中研究整个电网的同步稳定特性. 在环形网络中选取节点数N=100的电动机作为响应系统, 通过外部PMSM系统与电动机节点间的外部耦合函数, 实现电机网络的混沌抑制. 结果表明， 设计的反馈控制器结构简单, 控制效果较好.

1 PMSM动力学分析

1.1 PMSM数学模型

PMSM数学模型为三维自治系统[22], 其无量纲均匀气隙的数学模型为

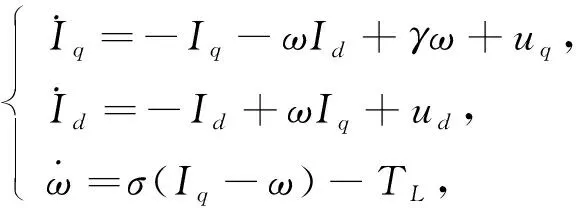
(1)

其中:Iq,Id,ω为系统状态变量, 分别表示q轴、d轴定子电流和转子角速度； 参数uq,ud,TL分别为q轴、d轴外加电压和外部扭矩.

本文考虑电机没有外力的情形[23], 即PMSM系统处于零输入状态, 系统(1)变为

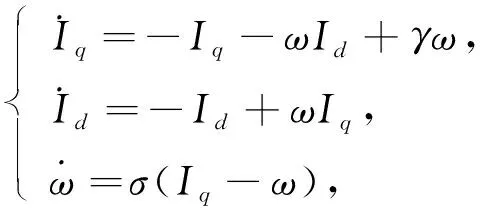
(2)

其中γ和σ均为正实数, 其多种组合可使均匀气隙PMSM系统出现混沌行为.

1.2 PMSM混沌行为

PMSM混沌行为的出现取决于分岔影响. 当系统参数σ=4.5时, 以γ为分岔参数作用于系统状态变量ω的分岔行为如图1所示.由图1可见,ω变量在参数γ的影响下出现分岔行为, 表明PMSM处于混沌运行状态.在图1中取σ=4.5,γ=25, 设置系统的初始值(Iq,Id,ω)=(0.1,2,-5), PMSM混沌相图和状态变量的时序分别如图2和图3所示.

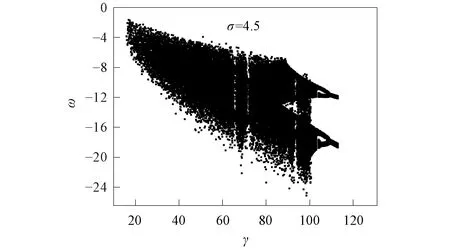
图1 PMSM分岔图Fig.1 Bifurcation diagram of PMSM

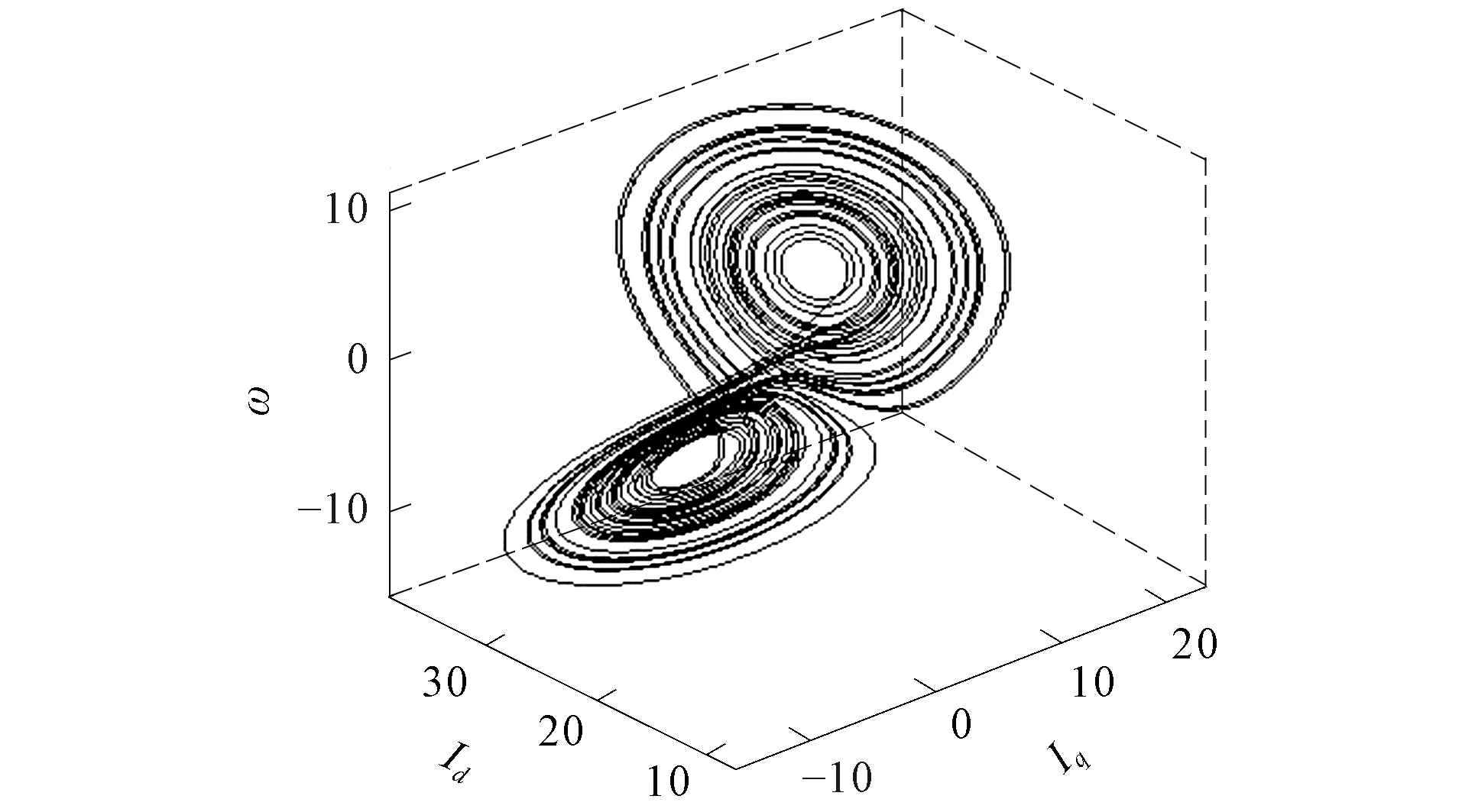
图2 PMSM混沌相图Fig.2 Chaotic phase diagram of PMSM

图3 PMSM状态变量的时序Fig.3 Time sequences of PMSM state variables

2 基于Lyapunov稳定性理论的非线性反馈控制器

由于PMSM在系统参数特定的范围内会产生混沌不稳定现象, 因此设计一种非线性反馈控制器, 并分析PMSM混沌系统在该反馈控制器作用下的动力学行为. 为计算方便, 令Iq=x1,Id=x2,ω=x3, 则PMSM数学模型(2)变为

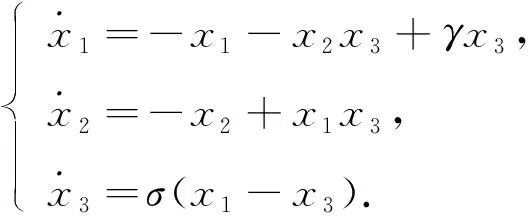
(3)

设计一个非线性反馈控制器

(4)

其中κ为非线性反馈系数.

因此, 具有非线性反馈控制的PMSM模型为

(5)

根据Lyapunov稳定性理论分析可知, Lyapunov函数的构造不唯一[12]. 本文将构造一个与PMSM混沌系统相关的Lyapunov函数V(x1,x2,x3), 若使PMSM混沌系统趋于稳定状态, 则需保证V(x1,x2,x3)为正定函数, 即V(x1,x2,x3)>0.构造函数

(6)

显然, 式(6)的函数是正定的.

根据定理1, 对式(6)求导可得

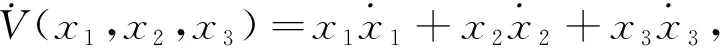
(7)

将式(4)和式(5)代入式(7)可得

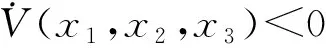
3 具有反馈控制器的单台PMSM动力学行为分析

下面用数值仿真证明系统参数σ大于反馈系数κ时的PMSM系统具有混沌抑制作用.采用步长h=0.001的四阶Runge-Kutta法[25]对具有非线性反馈控制的PMSM系统动力学模型(式(5))进行仿真实验, 设置系统参数σ=4.5,γ=25, 使PMSM在无反馈控制器的作用下处于混沌状态, 非线性反馈系数κ=4.38体现反馈控制器作用于PMSM的混沌行为.为观察非线性反馈控制器对已产生混沌现象的PMSM系统动力学行为的影响, 在t=30 s时加入反馈控制器, 图4为PMSM系统各状态变量间的时序. 由图4可见： PMSM系统在30 s时加入反馈控制器使混沌行为转变成稳定运行状态, 并使各状态变量逐渐稳定于零点状态, 即系统平衡点；ω在t=62.5 s后趋于0, 验证了非线性反馈控制器抑制PMSM系统的混沌行为, 进一步证明了该控制器的有效性.

设σ=4.5,κ=4, 观察PMSM混沌行为趋于稳定时间的长短, 在t=30 s时加入反馈控制器, 其状态变量的时序如图5所示.由图5可见，ω在t=36 s后趋于0, 与图4的ω变量相比, 图5的状态变量趋于稳定所需时间更短.因此, 当增大σ-κ之差时, PMSM混沌系统趋于平衡点所需时间更短, 表明PMSM越快趋于稳定运行状态.

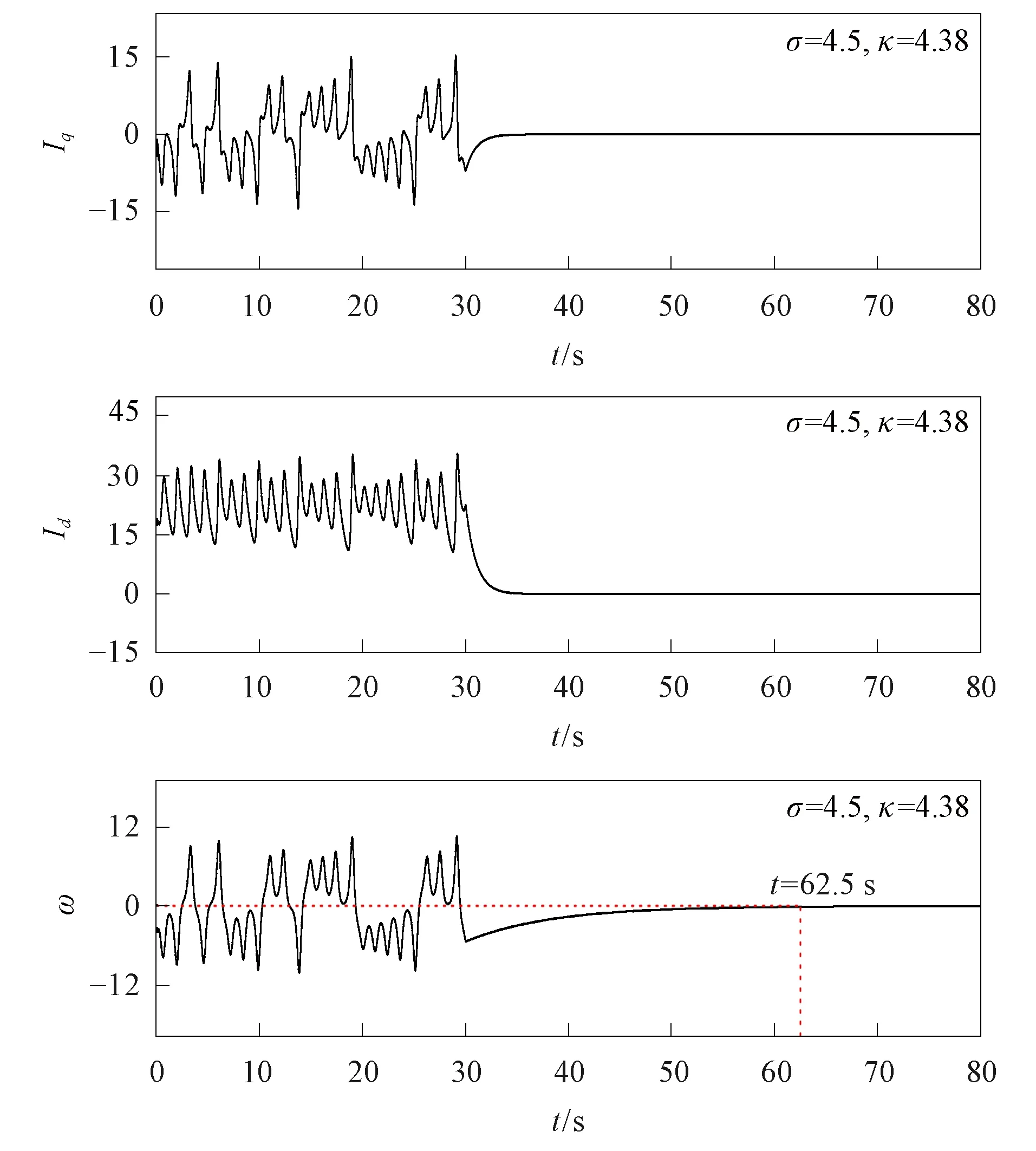
图4 当σ=4.5, κ=4.38时, PMSM状态变量的时序Fig.4 Time sequences of PMSM state variables when σ=4.5, κ=4.38

图5 当σ=4.5, κ=4时, PMSM状态变量的时序Fig.5 Time sequences of PMSM state variables when σ=4.5, κ=4

为进一步体现PMSM稳定状态对系统参数σ与反馈系数κ间的依赖性, 研究σ-κ的变化对PMSM系统混沌行为的影响.将σ-κ作为自变量, 选取系统运行时间t=40 s时角速度状态变量ω值作为因变量, 观察σ-κ与系统变量趋于稳定时间的快慢, 结果如图6所示.由图6可见, 当σ-κ=0.12时, 系统运行t=40 s时角速度ω未达到零点稳定状态； 当σ-κ=0.5时, 系统运行t=40 s时角速度ω已处于零点稳定状态, 表明系统参数σ和反馈系数κ之差越大, PMSM混沌系统趋于平衡点所需时间越短, 即PMSM混沌系统越快趋于稳定运行状态.

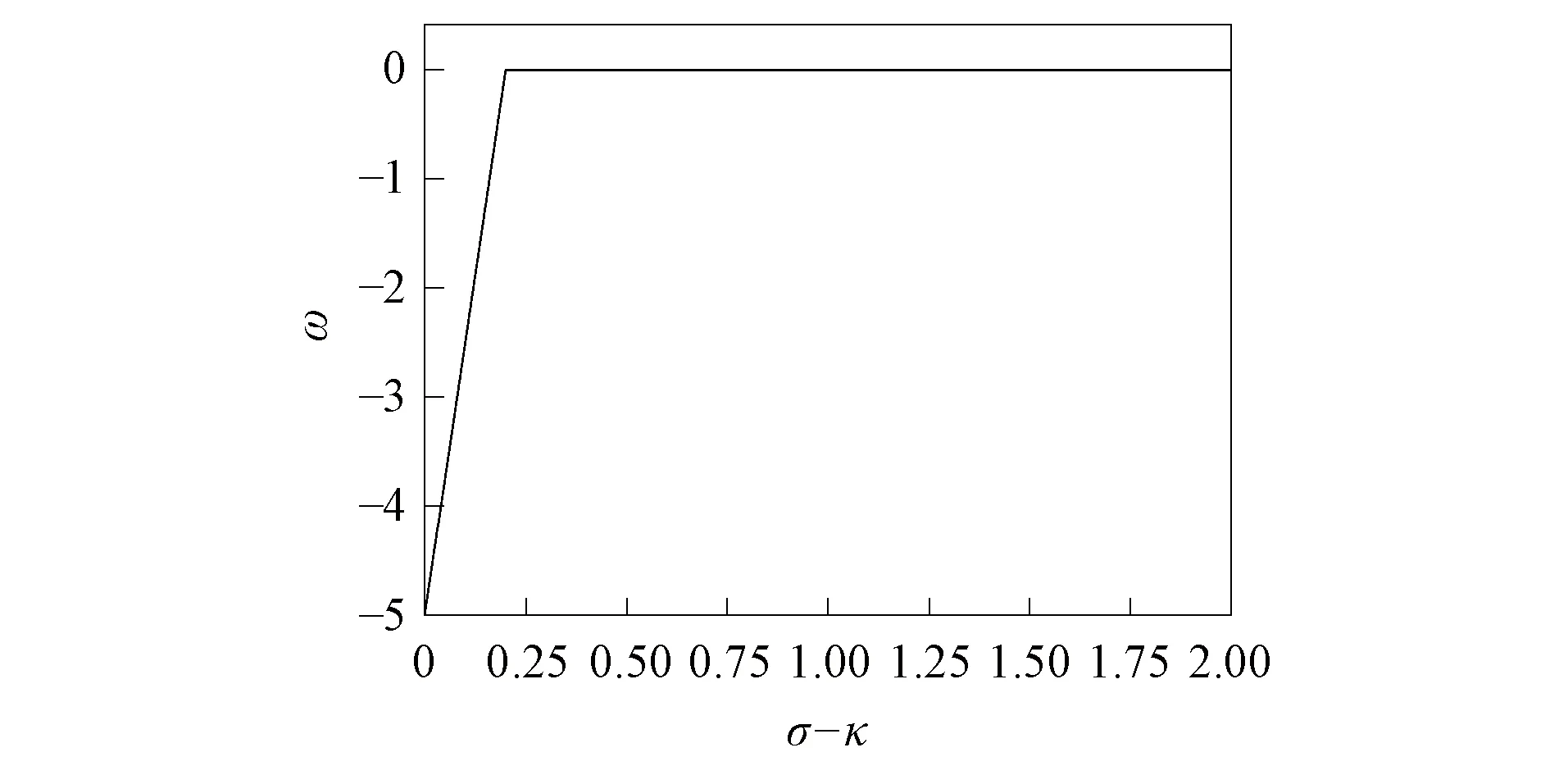
图6 σ-κ与角速度状态变量ω的关系Fig.6 Relationship between σ-κ and angular speed state variable ω

4 具有反馈控制器的PMSM诱发环形电机网络动力学行为

4.1 具有反馈控制器的PMSM耦合环形电机网络的数学模型

环形网络是电力系统网络中最常见的一种拓扑结构. 将具有非线性反馈控制器的PMSM作为一个驱动节点, 连接到由PMSM作为响应节点的环形拓扑网络中, 研究整个环形电机网络的同步行为. 环形网络由N个相同的PMSM混沌节点组成, 每个节点由一个n维动态系统构成, 节点间仅通过一个状态变量进行耦合, 其表达式为

Xi=f(Xi)+hi,

(9)

其中i=1,2,…,N,Xi=(xi,1,xi,2,…,xi,n)T∈n是网络中每个节点的状态变量,hi=(hi,1,hi,2,…,hi,n)T∈n是每个节点i的耦合输入信号, 包含节点间自身的内耦合项和外部其他系统节点连接的外耦合项.由于PMSM是三维自治动态系统, 因此网络中每个节点均为一个PMSM系统, 取q轴电流状态变量作为耦合变量, 根据式(9)可知n=3,Xi=(xi,1,xi,2,xi,3)T∈3, 则环形电机网络耦合的状态方程为

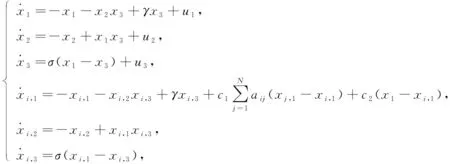
(10)

其中常数c1和c2分别表示环形网络的内耦合强度和外耦合强度,A=(aij)为由常数0和1构成的内耦合矩阵, 当环形网络节点i和节点j连接时,aij=1, 否则aij=0.假设环形网络模型节点数N=5, 具有非线性反馈控制器的电动机PMSM对其进行外部耦合, 图7为其模型示意图.由图7可见, 环形网络中相邻的节点间有连接, 即体现了环形网络的内耦合作用, 其邻接矩阵为

图7 电动机外部耦合环形网络示意图Fig.7 Schematic diagram of motor external coupling ring network

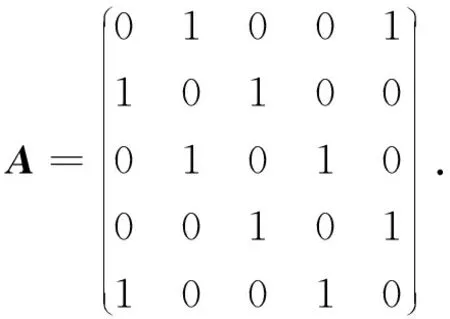
外部PMSM对环形网络具有全局耦合作用, 表明外部PMSM对环形网络中每个节点均有外耦合的影响, 这为具有反馈控制器的PMSM系统诱发网络中每个节点实现混沌抑制提供了可能性, 并最大限度节省了电力网络趋于稳定运行所需时间. 下面研究具有反馈控制器的PMSM系统诱发环形网络的稳定同步行为.

4.2 具有反馈控制器的PMSM诱发环形电机网络的混沌抑制

首先, 分析环形网络在无耦合连接作用下的动力学行为. 设网络节点数N=100, 每个节点的状态变量初始值各不相同, (Idi,Iqi,ωgi)T=(20,0.1,-5)T+0.1×(i-1)×(1,2,3)T.令网络自身的内耦合常数c1=0.1, 由于无外部耦合作用, 因此外耦合常数c2=0, 对环形网络进行数值仿真, 网络各节点状态变量的时序如图8所示.由图8可见, 在外部PMSM系统的耦合项未加入环形网络前(c2=0), 网络中各节点均处于混沌运行状态, 表明环形网络在内耦合项条件下是不稳定的.

图8 无外部耦合时的环形网络各变量时序波形Fig.8 Time sequence waveforms of each variable in ring network without external coupling

其次, 为研究外部耦合系统对原始环形网络的动力学行为影响, 改变外耦合常数值, 观察网络混沌行为达到混沌同步或混沌抑制的效果.令内耦合常数c1=0.1, 外耦合常数c2=1.58, 外部PMSM系统参数σ=4.5, 反馈系数κ=4, 其数值仿真结果如图9所示.由图9可见, 环形网络各节点状态变量在t=10 s后趋于一个稳定值, 即抑制了环形电机网络的混沌行为, 实现了振幅死亡的效果. 表明具有反馈控制器的PMSM系统可诱发环形网络实现混沌抑制, 进一步体现了非线性反馈控制器对单机PMSM混沌行为有抑制作用, 并可诱发电力网络实现振幅死亡的结果.

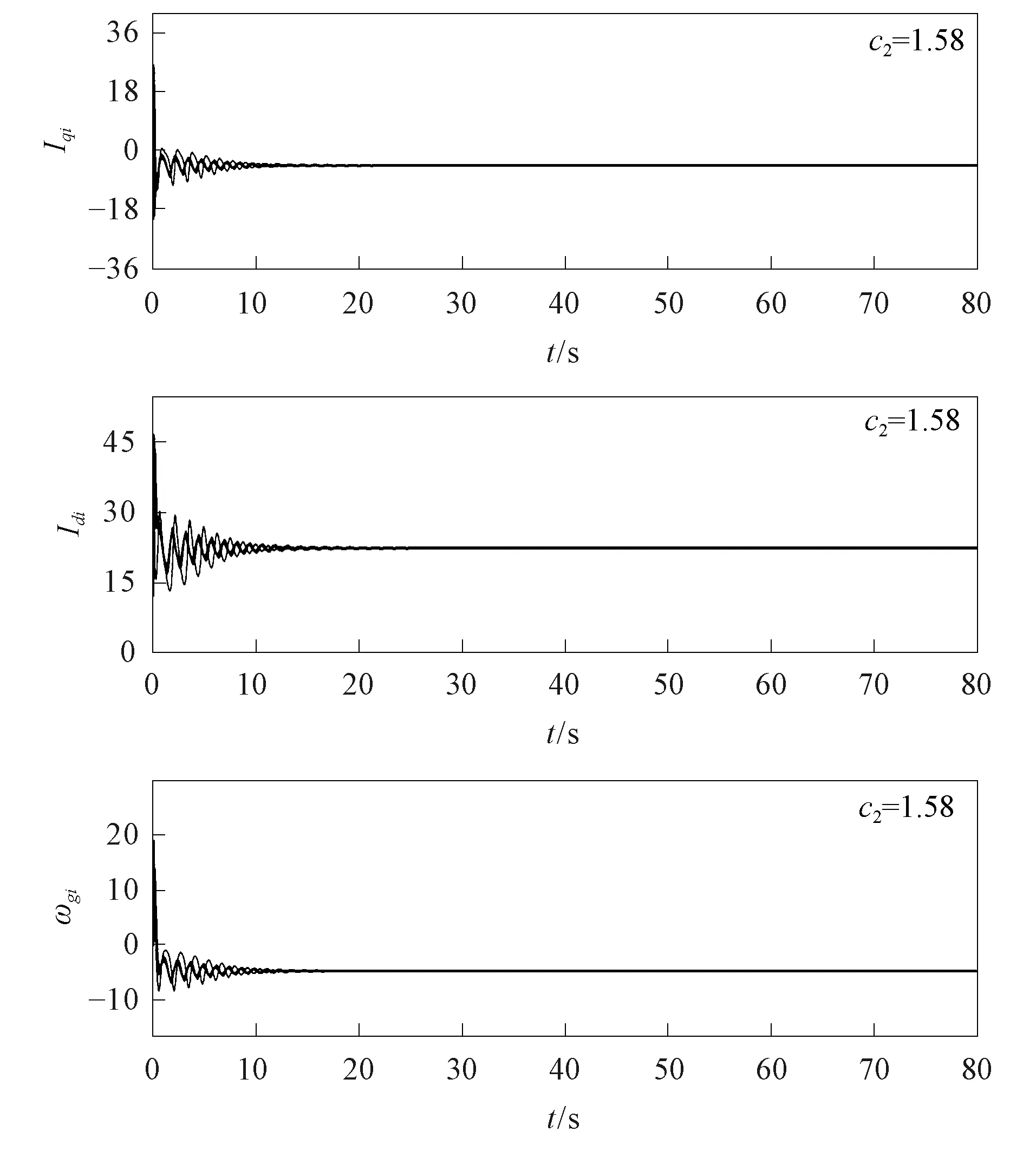
图9 外部耦合常数c2=1.58时的环形网络各变量时序波形Fig.9 Time sequence waveforms of each variable in ring network when external coupling constant c2=1.58

综上, 本文提出了一种非线性反馈控制器, 先用Lyapunov稳定性理论证明其正确性, 实现了永磁同步电动机PMSM系统各变量趋于零点的稳定状态; 再将这台已被稳定控制的PMSM作为电机网络的外部耦合系统, 加入节点由PMSM系统组成的环形网络中, 利用外部耦合常数诱发了环形网络实现振幅死亡的结果. 数值仿真结果表明, 该控制器有效, 控制效果较好, 并缩短了混沌系统达到稳定状态所需时间, 对电机网络稳定运行的研究提供了一种具有实际意义的控制方法.