巧用极化恒等式 解一类最值问题

浙江省金华市第六中学 (邮编：321000)

高考和竞赛试题中向量数量积的最值问题屡见不鲜，备受命题者青睐，灵活使用极化恒等式，一些高难度的题目将迎刃而解，本文举例说明极化恒等式在解决向量数量积最值问题中的应用，以期抛砖引玉.

1 极化恒等式简介

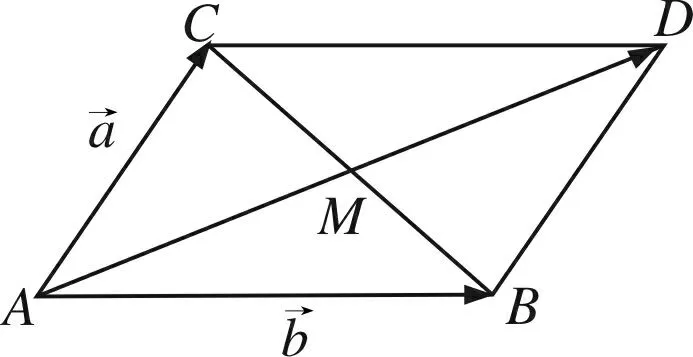
图1

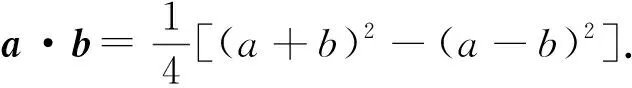
极化恒等式最显著的特征是两个向量必须能够转化为同起点的向量，它揭示了三角形的中线与边长的关系，搭起了向量与数量之间的桥梁，实现了向量与代数、几何的完美结合.

2 应用举例

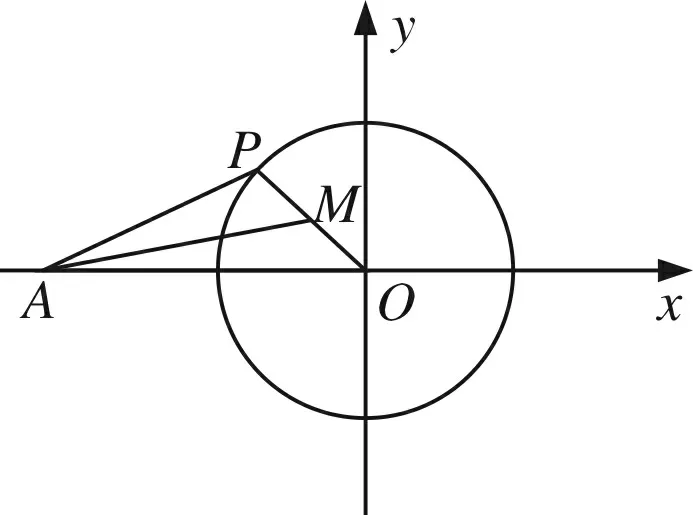
图2

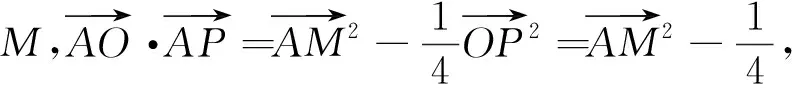
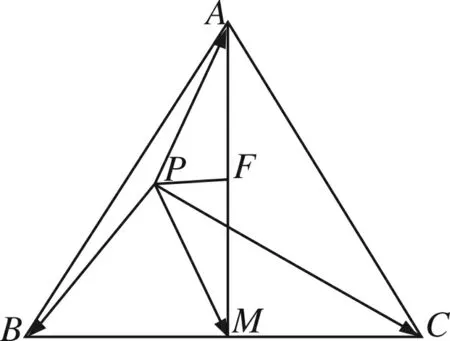
图3

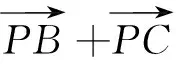
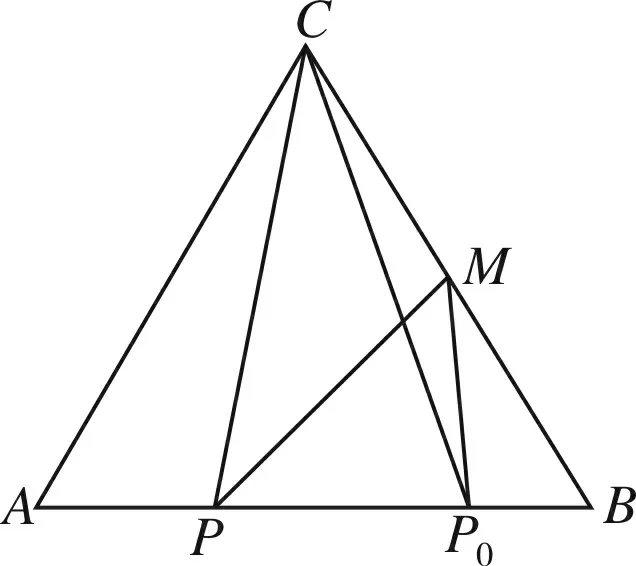
图4

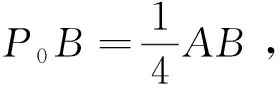
A.∠ABC=90° B.∠BAC=90°

C.AB=ACD.AC=BC

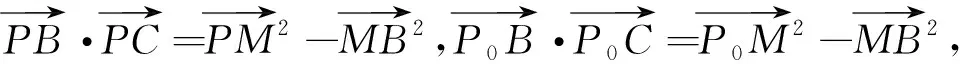
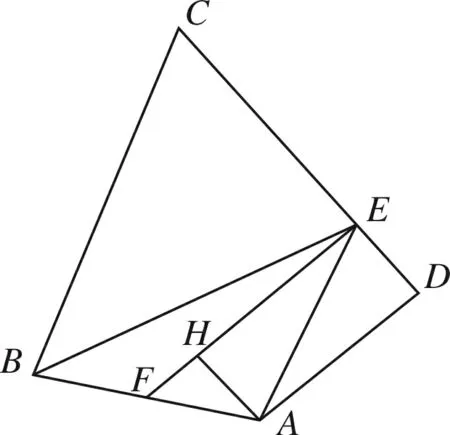
图5

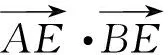
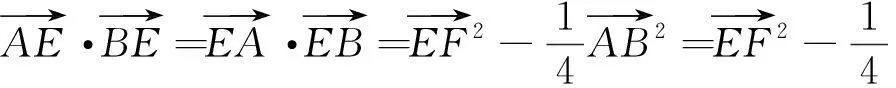
例5 (浙江省2018高中数学竞赛6)

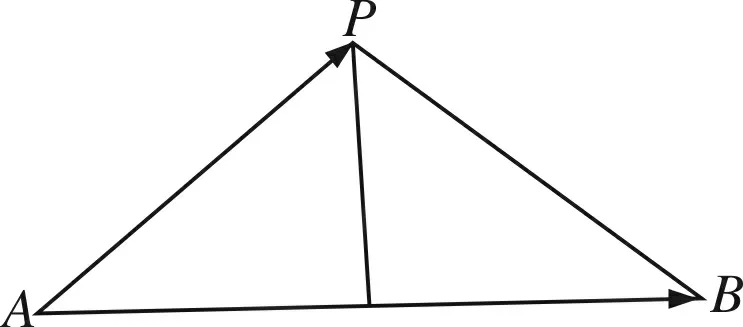
图6

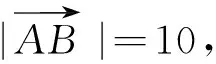
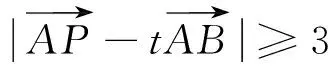
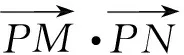
图7

使用极化恒等式求数量积最值的方法总结：

①把两个向量转化为同起点向量；②构建三角形，取连接两向量终点的线段的中点，把数量积的最值转化为某个向量模的最值；③利用题目中的特殊条件找到动点的最佳位置，进而求最值.

3 结束语

向量数量积的最值问题还可以可以从多角度去思考，如：定义法、坐标法、基底法和几何意义法等.当题目涉及到直线、平面或空间的一个动点，需要求两个向量数量积的最值的时候，引导学生利用极化恒等式去寻找解决问题的思路，把向量数量积的最值问题转化为某个向量模的最大值，进而找到该向量模取得最值时的动点的位置，有利于揭示向量问题的本质，有利于理解向量作为沟通代数与几何的桥梁作用，有利于领悟数形结合的数学思想，有利于分辨向量知识的源与流，从而摆脱题海战术，提高教学效率.