初中数学几何图形变化与分类案例分析
杨彦

【摘要】 初中数学中的几何图形教学具有很强的规律性,教师在授课时应该根据图形变化进行分类讨论,从而有助于学生更快更容易地理解和吸收知识. 本文按照几何形状、图形、位置的变化分类进行讨论,并且在教学课堂上不断地慢慢深入,对图形分类中出现的问题进行分析和总结.
【关键词】 初中数学;几何图形;图形变化;分类讨论;分析
一、引 言
新课标要求学生学习几何知识时能从原来比较复杂的各类图形分解出最基础的图形,要学会理解图形中的各元素及图形整体之间的关系,并根据最直观的感觉来思考问题. 本节课是初中几何数学一堂专门的复习课,教师根据学生平常考试和作业中涉及的、比较容易引起错误的习题进行归类和讨论,最后在教学课堂上讲课时不断地慢慢深入,对图形分类中出现的问题进行分析和总结,引导学生加深对几何图形的印象,并就根据什么规律如何分类进行讨论,从而把复杂的图形题分类归纳成最基本的图形,从而更有效地解决此类问题,培养学生敢于探索发现和创新的精神,以及求实、严谨的科学态度. 本文列举了三角形的周长问题、圆心距问题、圆的切线问题、复杂图形证明问题四个方面,并举例题来讨论几何图形的变化与分类问题.
二、教学设计——图形问题导入
在数学教学中,教师要引导学生对一些图形进行探讨,对其中一些相同或是类似的图形加以分析、对比、归纳及最后进行总结. 为此,在教学中的重点是教师要鼓励学生充分利用和挖掘出日常生活中图形变化的规律,并对造成这种现象和规律的原因分析探讨,最后寻找这类图形的相同点,那么学生解题就变得更加容易了. 例如,在初识几何图形的课堂中可以进行如下方式导入:
T:同学们写作业的时候用过方格纸作业本吗?S(大家异口同声):用过.
T:大家有没有注意观察作业本的方格纸是什么形状呢?我们现在投影仪屏幕上有一张作业本的方格纸(打出幻灯片),同学们看这个纸片是由什么样的图形组成的?S:由很多个小正方形组成.
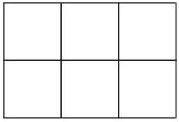
T:我拿出了其中的一部分(詳见图1),我请同学们数一下投影仪屏幕上所示的正方形有多少个?S:共有8个.
T:同学们你们是怎样数出来的,而且是能保证正方形的个数不多不少?S:可以分成边长为1和边长为2的正方形,然后数数每种不同边长的正方形分别有多少个,最后把这两种正方形相加起来就可以了.
T:同学们讲得很好,刚才这个方格纸的例子就是数学几何中的简单分类了,这就是对图形的最基础的分类讨论.T:那么再数数看有几个长方形呢?S:共有10个,可以把长方形分为三种,分别是宽为1,长为2;宽为1,长为3;宽为2,长为3,这三种类型的矩形,而后相加得出结果.
T:分类的标准应该是统一规范的,既不能重复,也不能遗漏. (评:学生通过对简单图形的识别,体会分类讨论的标准与原则,初步认识到分类讨论的必要性. )
教学点评:此案例采用的是问题图形导入法,首先在课堂上采用生活中常见的图形来抛出问题,激发了学生对该几何图形的回想,不仅加深了学生对图形印象,而且达到引起学生兴趣的效果;然后拿出具体图形让学生进行识别,同时导入分类讨论的思想,不仅使学生易于理解,更在潜移默化中灌输学生“分类讨论”这种数学中非常有用的思想方法,从而达到事半功倍的效果.
三、案例教学
1. 三角形的周长问题
例1 已知一个三角形为等腰三角形,且它的两条边长分别是3厘米和5厘米,请问:这个三角形的周长是多少?
S:周长分别是11厘米和13厘米.
T:为什么会出现两个答案呢?S:因为这个等腰三角形的两条一样长的腰长没有确定下来,可以是腰长为3厘米,也可以是腰长为5厘米,所以最后结果不同.
T:同学们讲得非常好,因为三角形的三边没有确定,所以三角形的形状大小也会发生变化.
教学点评:在平时做题中学生经常会犯“固定思维”的错误,说到等腰三角形很多人只会把它固定到某一种,而实际中“腰长”和“底边”并没有确定下来,因此不管是“3”还是“5”都有可能是“腰长”或者“底边”,但是此题也要考虑一种情况,如果两条边长分别是2厘米和5厘米,那么就只能有“腰长”是5厘米一种情况了,因为如果“腰长”是2厘米的话,那么另一“腰长”也为2厘米,此时“2 + 2 < 5”不符合三角形规律(三角形两边之和大于第三边).
2. 圆心距问题
例2 已知两个圆的半径分别为6厘米和9厘米,如果这两个圆相切,那么圆心距为多少?
S:内切是0,外切是15厘米.
T:为什么有两种结果?S:因为图形的位置没有确定,我们不知道两个圆是内切还是外切.
T:为什么要对几何图形进行分类呢?那是因为:
(1)几何图形形状不唯一确定.
(2)几何图形位置不唯一确定.
教学点评:在解题中因为几何图形位置不唯一确定,而且几何图形形状也不唯一确定,因此通过对几何图形的研究,使学生深刻理解对几何图形进行分类的原因,同时通过对分类的原因进行研究,初步学会怎样进行分类.
3. 圆的切线问题
例3 如图2,半圆O的直径ED = 12厘米,△ABC中,已知∠ACB = 90°,∠ABC = 30°. 半圆以2厘米每秒的速度由左边向右边滑动,在运动过程中,点D和点E始终都保持在直线CB上滑动,假设运动时间为t,且已知OC = 8厘米. 试问:当t为何值时,△ABC一边所在直线与半圆O所在的圆相切?
T:两种图形保持相切的关系有哪几种?
S:有四种关系,分别是线段AC和直线AB与圆左边相切和右边相切.
T:解题时同学们应注意圆心O在移动时候图形中位置的变化关系,考虑周全.
教学点评:在拿到此题时“两种图形保持相切的关系有哪几种”,首先要考虑到图形相切的定义,在圆与圆的关系中,相切定义既有内切关系也有外切关系,因此,审题时首先考虑到“内切”还是“外切”,在不能确定的情况下就要分为两种情况来讨论了;而本题中是考查直线与圆的位置关系,那么只有一种切线关系了,但是本题不同的是,本题中有“三条线段”,因此解答时应注意图形移动时到底是与线段AC,AB,还是BC相切.
4. 复杂图形证明问题
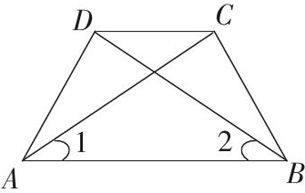
例4 如图3 ,已知在四边形ABCD中,AC = BD,∠1 = ∠2,求证: ∠CDA = ∠DCB.
T:根据已知条件我们可以知道AC = BD,∠1 = ∠2. S:是的.
T:我们可以从图3中看出线段AB是△ABD和△ABC的公共边,那么我们可以根据学过的三角形证明定理中的哪一个,得出这两个三角形的什么关系?S:根据三角形边角边(SAS)定理,我们知道△ABD和△ABC这两个三角形全等.
T:因为这两个三角形全等,所以对应角∠ADB和∠ACB也相等(分析: 根据基本图形的总结归纳,学生很容易发现例4图形中包含着轴对称型的全等三角形,所以学生能够证明哪几个三角形会是全等,明确目标后就能准确进行答题,从而提高答题的效率).
教学点评:很多同学在初拿到此题时会觉得无从下手,因为题设中给的AC,BD和∠1,∠2與要证明的∠CDA,∠DCB貌似没有任何关系. 但是仔细看图形就会发现,∠CDA = ∠CDB + ∠BDA,∠DCB = ∠DCA + ∠ACB,因此,只要证明∠CDB = ∠DCA,∠BDA = ∠ACB即可,在图形中,△ABD和△ABC有一个公共边AB,因此可以通过这个公共边来求出△ABD ≌ △ABC,同样方法求出△DCB ≌ △DCA,因此可以证明∠CDB = ∠DCA,∠BDA = ∠ACB. 此题给我们的经验是,在几何图形中当要求解的问题与题设没有明显的位置关系时,可以把要求解的问题拆分成一些基本的几何图形,根据基本图形中相对简单的图形关系来探索解题思路,化繁为简,从而完成求解.
四、总 结
图形分类讨论是一种十分灵活而又重要的解题法,它最关键的思路就是明确讨论的原因及相关的方法,就是要明白为什么去讨论,怎么去讨论. 只有思路清晰,那么心中就会有解题框架,答题就会条理分明,过程就能严密完整. 通过研究教学过程和效果,学生普遍能学习领会如何根据几何图形进行变化分类,但是在遇到一些复杂情况时,很多学生的分析还是不容乐观的,经常产生遗漏和重复讨论的现象. 另外,在实际教学中作者还发现很多学生在画图能力、空间想象能力、图形变化的操控能力等方面比较薄弱,这也是当今教育者在教学上需要改进的地方.

