一类具Holling Ⅱ型功能反应的食饵-捕食者模型的定性分析
范学良,雒志学,张宇功
(兰州交通大学 数理学院,甘肃 兰州 730070)
自然界中普遍存在的物种间相互作用是一种基本关系为捕食者-食饵的关系,揭示具有功能反应的捕食者-食饵相互作用的关系具有十分重要的意义和价值,许多学者对此已经做了大量的研究工作.
对于两种群相互作用的具有功能反应函数食饵-捕食模型,人们往往关心的是系统是否有孤立的周期解,换句话说就是系统是否有唯一的极限环,因为稳定的极限环对应稳定的种群的生态平衡.稳定的平衡态对种群的生存具有重要的意义.
文献[1]研究了具有Holling Ⅰ 型(它适用于藻类,细胞等低等生物)功能反应函数的捕食者-食饵系统:
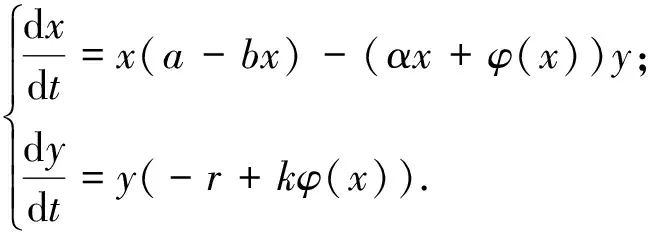
(1)
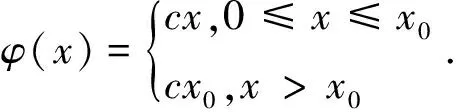
(2)
时,对系统的平衡点及极限环进行讨论.其中ω,a,b,k,r,α,β为正常数,l符号不定.
首先作时间变换(1+ωx)dτ=dt,则系统(2)变为
(3)
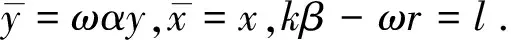
(4)
1 平衡点的性态
结论1 在平面上l<0或br-al<0时,系统(4)只有平凡平衡点O(0,0)及非平凡平衡点B(x1,0);当l>0且br-al<0时,系统有3个平衡点.
为了方便下面引理的证明,首先给出几点说明:
若线性系统在平衡点A处的特征方程为λ2+pλ+q=0,如果特征方程有2个异号的实特征根那么平衡点为鞍点,若特征方程有2个同号的实根那么平衡点为结点,若特征方程中的p>0,q>0则结点是稳定的.如果p<0,q>0则结点不稳定.如果特征方程有一对共轭复根,则平衡点为焦点.如果特征方程有一对纯虚根那么平衡点为中心焦点.详见文献[7].
结论2 在R2平面上,O(0,0)是鞍点,当al-br<0时,B是结点,当al-br>0时,B为鞍点;当l>0,al-br<0时,B为稳定的结点.
证明为了讨论平衡点的类型,首先将系统线性化,分别求出系统(4)对应点处的雅克比矩阵:

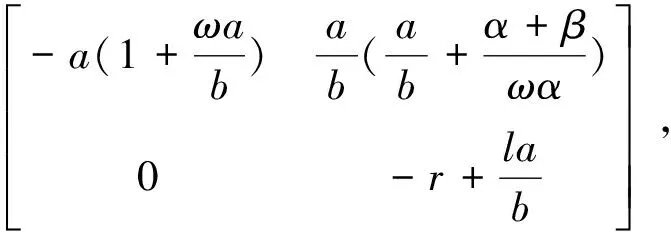
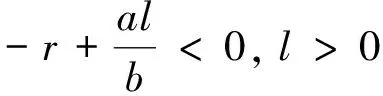
又当B点为结点时所对应的特征方程为

结论3 满足系统(4)的正初始条件的解是有界的.
证明考虑直线L:kx+y=N,沿着直线L有
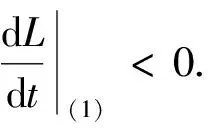
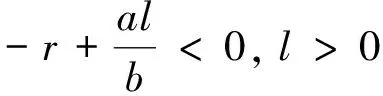
在P(x0,y0)点处的线性矩阵为
则P点处对应的特征方程为
令h=bx0(1+ωx0)-ωx0(a-bx0)+x0y0,则有如下结论5.
结论5 当l>0,x0
2 闭轨线的不存在性
定理1 由结论5可知当满足条件l>0,al-be<0且h≥0时系统平衡点是稳定的,系统(4)在R2内不存在极限环.
证明取Dulac函数B(x,y)=xmyn,则有
令
H(x,y)=-2bωx2-(b+aω+l(n+1))x-r(n+1)-xy,
T(x)=-2bωx2-(b+aω+l(n+1))x-r(n+1).
要使得H常号,只需T(x)=-2bωx2-(b+aω+l(n+1))x-r(n+1)无实根或仅有唯一的实根,要满足上述条件从而只需f(n)=[b-aω-l(n+1)]2-8brω(n+1)≤0,
令n+1=N,则有
f(N)=l2N2-[2l(b-aω)+8brω]N+(b-aω)2≤0.
为了能选择N0使f(N0)≤0,必须保证f(N0)=0至少有一实根.
即要求[2l(b-aω)+8brω]2-4l2(b-aω)2≥0,可得lb-laω+2brω≥0,又因为l>0, -br+la<0可得lb-laω+2brω≥lb-brω+2brω≥0.即当l>0,-be+la<0时,f(N0)=0有2个实根或有2个重根.
若有2个实根N1,N2,当N1
3 极限环的存在及唯一性
极限环的存在性,可以通过构造Bendixson环域的方法进行证明.
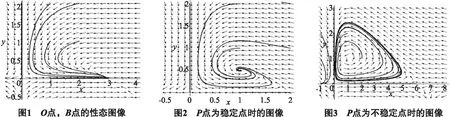
由结论5知当满足条件l>0,x0 又x轴y轴都是系统(4)的轨线,这样由直线x=x1,my-lx-k=0,x轴,y轴围成环域G的外境界线,G的内部无其他奇点,O点和B点均为鞍点,由Bendixson环域定理可知,G内至少存在一个包含R点的极限环. 极限环的唯一性的证明,我们采用张芷芬定理来证明,为此,首先要把系统(4)化为Liendard方程. (5) (6) 再令(x0eξ+m)y0dt=dτ,变换后ξ,η,τ,仍记为x,y,t,进而系统(4)化为Lienard方程. 系统化为 容易检验: 2)φ(0)=e0-1=0,φ(y)′=ey>0; 3) 因为 [(b(1+ωx)-ω(a-bx))(x+m)+(a-bx)(1+ωx)](x+m)(-r+lx)+2bωx2(x+m)2(-r+lx)+[(b(1+ωx)-ω(a-bx))(x+m)+(a-bx)(1-ωx)](r-2lx) 由于右边的函数是单调递增的所以左边的式子也是单调递增的.由张芷芬定理可知,系统至多存在一个极限环,若存在必稳定. 定理2 当满足下面的条件时. 1)l>0,h<0;其中h=-bx0(1+ωx0)+ωx0(a-bx0)-x0y0; 2)A(x)′B(x)-A(x)B(x)′>0则系统(1)在R2内正平衡点外围有唯一的极限环且稳定. 当参数取a=3,b=1,ω=1,α=1,β=5,k=1,r=4,l=1时,参数满足结论1、结论2的条件,此时可以从图1可以看出O点处向量场是远离O点的,由文献[7]可知O点为鞍点,B(3,0)点处的向量场(箭头所趋向的方向)是趋向于B点的,所以由文献[7]可知B稳定的结点. 当参数取a=2,b=1,ω=1,α=1,β=2,k=2,r=2,m=3,l=2时,参数满足定理1的条件,根据图2向量场的趋向可以看出P点是一个稳定点,所以没有极限环. 当参数取a=6,b=1,ω=1,α=1,β=8,k=2,r=4,m=9,l=4时,由图3可以看出向量场形成一个极限环.所以当P点为不稳定的结点时,存在1个极限环. 参考文献: [1] 王育全. 一类具 HollingⅠ型功能反应的食饵-捕食者模型的极限环及平衡点的全局稳定性[J].怀化学院学报, 1989(5):6. [2] 陈柳娟, 孙建华.具 Holling 第 Ⅱ 类功能性反应的捕食者-食饵系统的定性分析[J].生物数学学报, 2003, 18(1): 33-36. [3] 刘启宽, 张兆强, 陈冲.一类具有功能反应的食饵-捕食模型的定性分析[J].重庆理工大学学报: 自然科学版, 2010 (1): 118-122. [4] 陈晓鹰, 朱婉珍.具有 HollingⅡ 型功能性反应的捕食者-食饵种群 SIS 模型定性分析[J].厦门大学学报: 自然科学版, 2005, 44(1): 16-19. [5] 匡奕群, 邱梅青.一类具功能反应的食饵-捕食者模型的定性分析[J].生物数学学报, 2008, 22(4): 629-633. [6] 刘敏,陈斯养.具有收获和分段常数变量的捕获-被捕食模型的分支分析[J].云南师范大学学报:自然科学版,2013,33(5):41-47. [7] 马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996. [8] 马知恩.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.
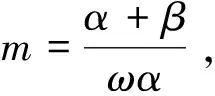

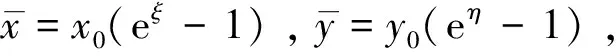
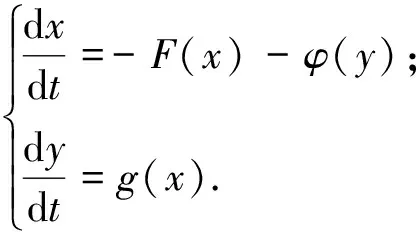
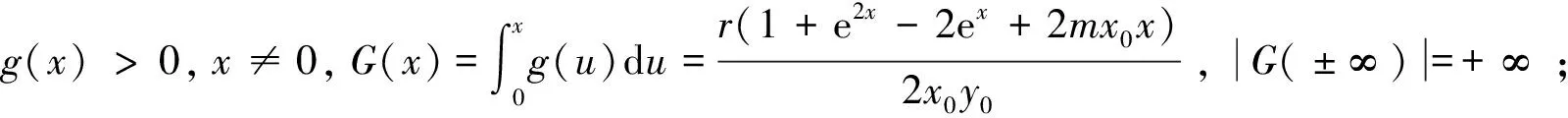
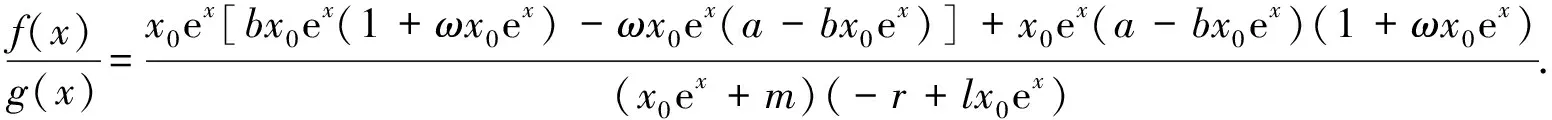
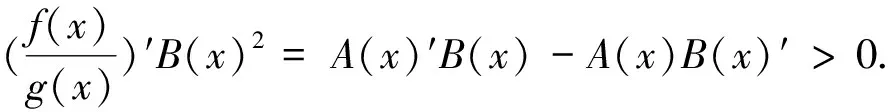
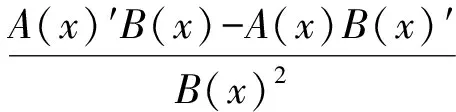
4 用Maple软件进行数值模拟