城市圈互斥共生演化博弈研究
孙 锐,王源昌,李 超
(云南师范大学 数学学院,云南 昆明 650500)
20世纪80年代起,伴随着工业化进程的不断加速,我国的城市化进程也进入了快速发展期.进入21世纪,我国城市化进程进一步加快,城市圈大规模建设阶段也已经到来.与此同时,伴随着这场剧烈的变革,城市圈建设中不可避免的地出现了大量的经济社会矛盾需要予以解决.而在新的城市群建设中,如何解决城市圈中城市之间错综复杂的关系与联系,减少城市之间互斥,引导城市走向合作共生,成为重中之重的关键.
城市圈中城市的互斥与共生是一场长期的动态的博弈,而且最终达到的平衡也是一种动态的均衡.这就需要我们运用演化博弈这一新的理论去研究城市圈中的互斥共生.
1 演化博弈理论基础
文献[1]中定义,如果I是一个稳定策略(ESS, evolutionary stable strategy),它必须具有下列性质:如果群体中几乎所有个体都采取了I策略,那么采用这种策略的适应度必然将高于任何可能出现的其它策略的适应度,否则其它策略将会改变整个种群,I也就不可能稳定.假设这样一个群体,它主要由采取I策略的个体组成,并且伴随存在着极小比例p的采取不同策略J的个体,W0表示个体起始的适应度,W(I)和W(J)分别表示I策略和J策略所带来的适应度;E(I,J)表示个体选择I策略而对手选择J策略所带来的回报.因而有:
W(I)=W0+(1-p)E(I,I)+pE(I,J),
(1)
W(J)=W0+(1-p)E(J,I)+pE(J,J).
(2)
由于I是ESS,那么W(I)>W(J).又因为p<<1,这就要求对所有的J≠I有:
E(I,I)>E(J,I)
或者
E(I,I)=E(J,I),且E(I,J)=E(J,J).
(3)
这就是策略I演化稳定策略的定义.
演化博弈中博弈方策略类型的比例一直处于动态变化,博弈方通过学习模仿来调整自身的策略,通常情况下,博弈方学习模仿的速度取决于2个因素:一是模仿对象的数量大小(可用相应类型博弈方的比例来表示),因为这关系到观察和模仿的难易程度;二是模仿对像的成功程度(可用模仿对象策略得益超过平均得益的幅度表示),因为这关系到判断差异的难易程度和对模仿激励的大小.而复制动态正是表示了某种确定策略在某群体中被采用的频率或某个个体采用的概率变化的动态微分方程.下面给出一种复制动态微分方程的推导过程:
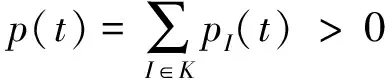
(4)
将总体平均收益表示为E(x,x)是因为这个收益与混合策略x针对自身采用时得到的收益是相同的.
假设收益代表的是博弈对个体适应性影响的增量效应,该适应性是用单位时间的后代数量来度量的.还假设,每个后代继承了他父母的单一策略.如果生育是连续不断的,那么按规定选择纯策略i的人们在任何时候t的出生率为β+E(i,x),这里的β≥0是总体中人们的背景适应性(与博弈的结果无关).假设所有个体的死亡率δ是相同的.用点表示时间导数,并去掉时间自变量,就能产生如下的动态方程:
对恒等式p(t)xi(t)=pi(t)两边取时间的导数,得到
[β+E(i,x)-δ]pi-[β+E(x,x)-δ]pxi,
两边同除以p就得到
因此,对应的复制动态方程为
(5)

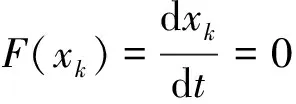
这就是动态复制微分方程的 “稳定性定理”.
接下来以演化博弈理论中的这2个基本概念为理论基础,来进一步研究城市圈中城市间互斥共生演化博弈模型.
2 城市圈中城市间互斥共生演化博弈模型
随着我国城市化的不断加深,城市经济圈的形成已经成为城市化加深的重要标志,而且在同一城市圈中的城市之间的联系与影响也逐渐增加.由于城市圈中城市之间存在着众多的利益冲突,每个城市为了自身利益的最大化而进行着激烈的竞争,使得城市间往往处于互斥的状态.同时,由于存在进行分工与协作产生规模效应使合作双方“共赢”的情况,城市圈中城市也存在合作共生的可能.在博弈的过程中,可以把城市作为一个存在有限理性的博弈方,它会根据自己以前的策略与圈内其它城市的策略来进行学习进化,从而不断调整自己的策略.所以其选择策略行为的过程可以视为生物学意义上的演化博弈过程,每次策略的选择都是在考虑其他成员的策略与自身策略的适应性下做出的.因此可以用一个演化博弈模型来分析城市圈中城市互斥共生行为及其进行的动态调整.
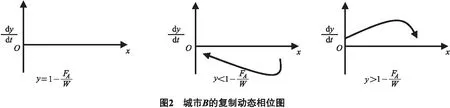
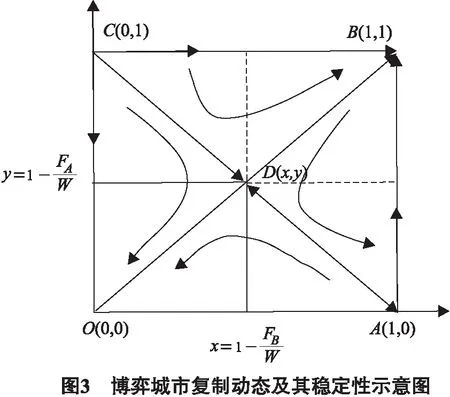
为了方便研究,考虑两城市之间的演化博弈模型,假设在某城市圈中存在城市A与城市B,他们之间具有一定的联系,假设它们的策略选择空间为互斥、共生.当城市A与城市B都采用互斥策略时(例如各自为政带来的引资大战、重复建设、市场分割与贸易壁垒,使城市间出现激烈竞争),则根据各自的经济实力与行政能力分别可以得到支付VA和VB;当城市A与城市B都采用共生策略(例如产业合作与城际分工,资源与环境合作,信息与技术的共享),从而使两城市达到共赢,双方都得到在原来基础上得到额外的收益增量W;当城市A与城市B采用的策略不同时,即一方选择共生策略而另一方选择互斥策略(在现实中出现这种情况往往是两城市达成合作协议但其中一方暗中违约),则采用互斥策略的城市能够得到更多的收益增量Fi(i=A,B),而采用共生策略的城市则会造成Fi(i=A,B)的损失,并假设FA 表1 不同策略下参与主体双方的支付函数 根据上文分析,可以构建博弈双方的收益期望函数,其中城市A采用互斥策略的期望收益为: EA1=yVA+(1-y)(VA+FA). 而城市A采取共生策略的期望收益为: EA2=y(VA-FA)+(1-y)(VA+W). 则城市A的平均收益为: EA=xEA1+(1-x)EA2. 这样根据复制动态方程,经过运算后得到城市A采取互斥策略的复制动态微分方程为: F(x)=dx/dt=x(EA1-EA)= x(1-x)(FA-W+Wy). (6) 由上式对x求导得: F′(x)=(1-2x)(FA-W+Wy). 令F(x)=dx/dt=0,解得x1=0,x2=1,y=1-FA/W. 由复制动态微分方程稳定性定理及演化稳定策略性质知,当F(x*)=0,F′(x*)<0时,x*为演化稳定策略.以下对y值进行讨论: 1) 若y=1-FA/W,则F(x)=dx/dt=0,F′(x)=0,即所有y轴水平都是稳定状态,当B城市互斥的概率达到y=1-FA/W时,城市A采取任何策略的可能性都是稳定的. 2) 若y<1-FA/W,对x1=0,x2=1,有F′(0)<0,F′(1)>0,此时x1=0为全局唯一的演化稳定策略;即当城市B采取互斥策略概率达不到一定程度并呈下降趋势时,城市A采取互斥策略的可能性逐步减小,选择共生策略将是城市A的最优选择. 3) 若y>1-FA/W,对x1=0,x2=1,有F′(0)>0,F′(1)<0,此时x2=1为全局唯一的演化稳定策略;即当城市B采取互斥策略概率达到一定程度并呈增大趋势时,城市A采取互斥策略的可能性逐步加大,最终确定为互斥策略. 城市A的复制动态相位图如图1所示. 同理,可以得出城市B采用互斥策略的复制动态微分方程为: F(y)=dy/dt=x(EB1-EB)= (7) 由于城市B与城市A是对称的,类似上文分析可以利用复制动态微分方程稳定性定理及演化稳定策略性质来得到类似的结果.其城市B的复制动态相位图如图2所示. 综合上文城市A与城市B的复制动态相位图,把二者结合起来,将博弈双方的复制动态关系用一个二维的平面坐标来表示,最终得到图3. 从图3的二城市互斥共生演化博弈复制动态相位图中,可以看出城市的动态演化过程.在图3中,由点A和点C以及临界点D构成的两端折线,它们是使城市动态演化博弈形成两个完全不同状态的分界线.其中OADC区域演化博弈将收敛于O点,即相互共生;而ABCD区域的演化博弈将最终收敛于B点,即相互排斥. 从以上的演化博弈模型与复制动态相位图可以知道,城市圈中城市的博弈可以向2个方向进行演化,既可以采取互斥策略,也可以采取共生策略,而这2种策略都是进化稳定的策略.这一结论正好可以用来解释在现实世界中城市圈的行为.在没有内部信任与外部约束的情况下,城市与城市政府就会倾向于考虑个体利益而不考虑集体利益,只考虑短期利益而不考虑长期利益,则必然导致城际恶性竞争并且城市间互斥的结果.而在双方都有足够的诚意进行合作共生,即便存在一些扰动,在多次博弈后,共生的策略也会成为唯一的稳定策略. 在城市圈城市间互斥共生演化博弈策略的稳定性探讨中,模型的参数变化对最终城市策略的选择有重要的影响.在二维复制动态相位图中可以看出,城市演化博弈过程与结果受到城市双方初始状态的影响.当初始状态在OADC区域,演化博弈系统将最终收敛于O(0,0)点,即城市间将会采取相互共生策略;当初始状态在ABCD区域时,城市双方的演化博弈将收敛于B(1,1)点,即城市间将会采取相互排斥策略.而相同的初始状态会因为临界点D的变化而向不同的均衡点收敛,这是因为点D的变化会带来上文提到的2个区域的变化,因而使得初始状态向着不同的均衡点收敛,形成路径不同的进化稳定状态. 因此,可以从点D的表达式x=1-FB/W,y=1-FA/W来讨论各参数变化对系统进化行为的影响和采取相应的控制措施.由于只有通过合作共生,城市圈的发展才能节能高效,长远地可持续发展,其中的每个城市才能达到双赢的结果.所以为了使城市间博弈最终收敛于合作共生,应该使区域OADC尽量大,即使得D点尽量接近B点.为了达到这一目的可以从两方面入手. 参数W表示为城市圈中两城市都采取共生策略时,给企业双方带来的利益的增加.当W增加时,D点坐标会向B点移动,那么区域OADC的面积随之增大,区域ABCD的面积随之减少,这将导致城市演化博弈以很大概率向共生稳定策略收敛.这在现实世界中表现为:当城市间采取共生合作策略所带来的利益越大,城市间也就更趋向于合作共生.为了提高W,必须加强城市间的联系,建立起城市间差异化产业分工、互补与合作的体系,就能够节约生产和运输成本,共享最新的信息与技术,从而有效利用城市圈聚集经济和规模经济,使得共生取得的收益达到最大.需要注意的是,在产业分工中,由于单个城市从自身利益出发,难免会有些困难与抵触,这就需要上一级政府从战略高度出发,统筹全局,使得各城市间职能分工明确,主导产业定位合理,实现资源优势互补,共同提高协作共生带来的利益. 参数FA与FB表示当城市圈中城市采取不同的策略时,采取互斥策略的城市获得收益增加,而采取共生策略的城市的收益将减少.从表1支付可以看出同一城市采取不同策略对该城市带来的收益增加和减少是相同的.例如当城市A采取互斥策略,而城市B采取共生策略时,FA表示城市A收益的增加,FB表示城市B收益的减少;反之,FA表示城市A收益的减少,FB表示城市B收益的增加.随之FA与FB的增加,D点坐标会向原点O点移动,那么区域OADC的面积随之减小,区域ABCD的面积随之增加,那么城市双方将极大可能采取互斥策略为进化稳定策略,这在现实世界中表现为:在城市达成共生合作的合约后,如果违约一方将能得到足够大的利益,而守约一方将因为对方违约遭到巨大损失,那么违约方将极大可能铤而走险继续违约,而守约方也终将放弃合约.而随着FA与FB的减小,D点坐标会向原点B点移动,那么区域OADC的面积随之增大,区域ABCD的面积随之减小,那么极大可能城市双方将采取共生策略为进化稳定策略.即为了使城市圈中的城市能够长期稳定的共生合作,城市双方应该签订有约束的协议,并由上一级政府进行监督执行,即对违约一方进行严厉惩罚,尽量减少其通过违约带来的收益;而对守约一方进行物质激励,减小其损失,这样就同时减小参数FA与FB的值,从而使得城市双方达到合作共生的稳定结果. 在图3中,由点A和点C以及临界点D构成的两端折线是使城市动态演化博弈指向2个不同结果的分界线.当已知A城市的采取互斥策略的概率x,可以根据分界线推出B城市采取互斥策略的y的范围,使得最终城市走向合作共生. 用“两点式”求出线段方程为 (8) 当城市A采取互斥策略的概率确定为PA,如何确定城市B采取互斥策略的概率PB取值的范围,使双方最终收敛于合作共生的结果.下面进行讨论: 1) 当0≤PA<1-FA/W时,B城市互斥策略的概率为PB∈[0,-PAFA/(W-FB)+1),最终可以在经过一段时间博弈后最终达成城市间的共生. 2) 当1-FA/W 我国经济发展与城市化建设的长期性与艰巨性决定了建设城市圈合作共生机制的重要性.运用演化博弈的基本理论对城市的策略行为进行分析,得出了影响城市进行互斥还是共生的关键是合作共生产生的额外收益的大小,和违反合作协约时的收益与损失的大小.这要求上级政府和城市圈中的城市统筹安排,扩大合作收益,建立良好的信用机制,对违约行为进行有效惩罚制止.并且通过了解博弈对方的合作意图,来调整自身的策略也是达到合作共生的关键,这就要求城市间加强联系,减少误判,基于此构建的演化稳定策略也终将实现区域城市圈间的合作与共生. 参考文献: [1] SMITH J M, PRICE G R. The logic of animal conflicts[J].Nature,1973, 246: 15-18. [2] SMITH J M. Evolution and the theory of games[M].Cambridge:Cambridge University Press, 1982. [3] MAYNARD SMITH J. The theory of games and the evolution of animal conflicts[J]. Journal of Theoretical Biology, 1974, 47(1): 209-221. [4] WEIBULL J W. Evolutionary game theory[M].Cambridge:Massachusetts Institute of Technology Press, 1997. [5] 郭本海, 方志耕, 刘卿. 基于演化博弈的区域高耗能产业退出机制研究[J].中国管理科学, 2012, 20(004): 79-85. [6] 刘伟兵, 王先甲. 进化博弈中多代理人强化学习模型[J].系统工程理论与实践, 2009 (3):28-33. [7] 达庆利,张骐骥. 有限理性条件下进化博弈均衡的稳定性分析[J].系统工程理论方法应用, 2006 (6): 279-284. [8] FOSTER D, YOUNG P. Stochastic evolutionary game dynamics [J].Theoretical Population Biology, 1990, 38(2): 219-232. [9] 黄敏镁. 基于演化博弈的供应链协同产品开发合作机制研究[J].中国管理科学,2010(12): 163-170. [10] 迈克尔 波特.竞争战略[M].陈小悦,译. 北京:华夏出版社,1997.
3 演化稳定策略求解
y(1-y)(FB-W+Wx).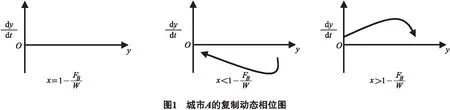
4 模型的参数分析与控制措施
4.1 参数W
4.2 参数FA与FB
4.3 博弈双方的控制
5 结语


