基于反推法的机电系统自适应模糊控制*

张 营，李 鹏，郭亚军

(1.济宁学院 物理与信息工程系，山东 曲阜 273155;2:中国电子科技集团公司第三十八研究所，合肥 230088;3:南京理工大学 机械工程学院，南京 210094)

0 引言

永磁交流伺服机电系统是数控装置和机床机械传动部件间的联系环节，它将微电压信号转化为机械传动，在数控机床系统中起着重要作用。在控制对象转动惯量较小且跟随角加速度较低，而传动装置有较大刚度的情况下，机械结构的影响可以忽略［1-3］。但在控制对象具有较大转动惯量，且系统具有较宽通频带的情况下，系统运动时传动轴的弹性扭转变形将会导致明显滞后［4］，影响系统控制精度。因此传统的控制策略很难达到满意的效果，如PID等。近年来，伺服耦合系统控制策略研究获有了较大发展，比如滑模控制［5］、伺服自适应控制［6］、模糊控制［7］和反推控制等［8］。其中反推设计方法以其易于与自适应控制、智能控制等技术相结合，能够消除参数时变和外界干扰对系统性能的影响而受到广泛关注。反推法将复杂的系统分解为若干个子系统，通过引入虚拟控制量来逐步进行控制器的设计，最终确定控制律，从而实现对系统的有效控制［9-11］。

20 世纪60 年代，美国学者Zadeh 首次提出模糊集理论后，模糊逻辑控制策略便引起国内外学者的重视，并用于非线性系统和不确定系统的控制设计［12］。因此本文以机电耦合系统的位置控制为研究对象，针对系统的不确定参数采用自适应模糊控制策略，通过对数学模型进行反向递推逐步选择Lyapunov 函数，设计了基于自适应模糊的反推位置控制器，在确定电流环和速度环带宽的情况下，保证了系统的稳定性和跟踪精度。

1 永磁交流伺服机电系统模型的建立

1.1 电机建模

假设:忽略铁心饱和效应;气隙磁场呈正弦分布;不计涡流及磁滞损耗;转子上无阻尼绕组，永磁体也无阻尼作用;控制方式采用定子电流的d 轴分量即励磁电流Id= 0。

根据假设条件，建立转子即d-q 坐标系下的模型如下:

式中，uq是定子电压;iq是定子电流;Ls是定子绕组自感(Ls= Ld= Lq);Rs是定子绕组的内阻;ωM是转子旋转角速度;Ψf是转子磁链;pn是极对数;Te是输出转矩;TL1是等效的磁阻转矩;BM是阻尼系数;JM是电机的转动惯量;Kt是电磁转矩系数。

1.2 机械传动子系统

子系统的输入用θM表示，子系统的输出用转角θL表示，则可得方程式如下:

式中，JL是折算的转动惯量，BL是折算的粘性摩擦系数，KL是总刚度，i 是减速器的减速比。

假定电流环为PI 控制且电流环响应速度比速度环和位置环快很多，因此可将电流环近似看作为比例环节，且其比例系数为1。速度环采用IP 控制，取各积分输出［x1，x2，x3，x4，x5］为状态变量，经简化最终可得到机电耦合伺服系统状态空间模型如(5)式所示。

式中，KVI是积分系数;KVP是比例系数;ω*M(s)是速度参考值。

为了便于反向递推，式(5)可写为:

其中:

2 自适应模糊反推控制器设计

根据反推原理，设计步骤如下:

步骤1:机械位置误差变量e1为:

选取Lyapunov 控制函数:

对式(12)求导:

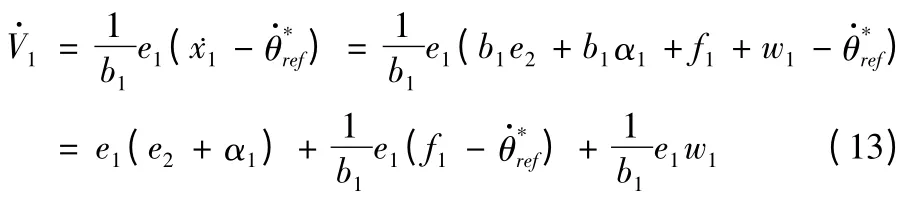
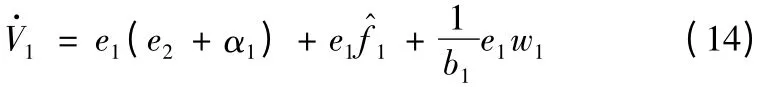
函数f^1的模糊系统，则:

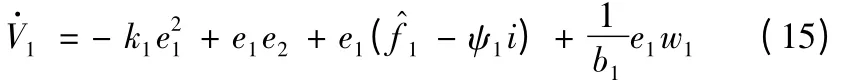
其中:

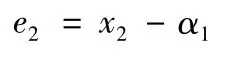
步骤2:选取Lyapunov 函数:

对V2求导，利用(16)式可得:

其中

步骤3:选取Lyapunov 函数:

对V3求导，由(17)式可得:

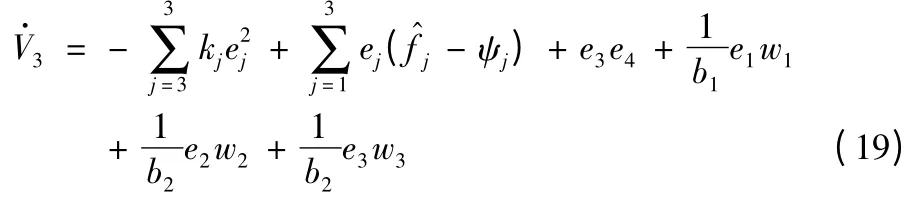
步骤4:选取Lyapunov 函数:

对V4求导，由(19)式可得:

步骤5:选取Lyapunov 函数

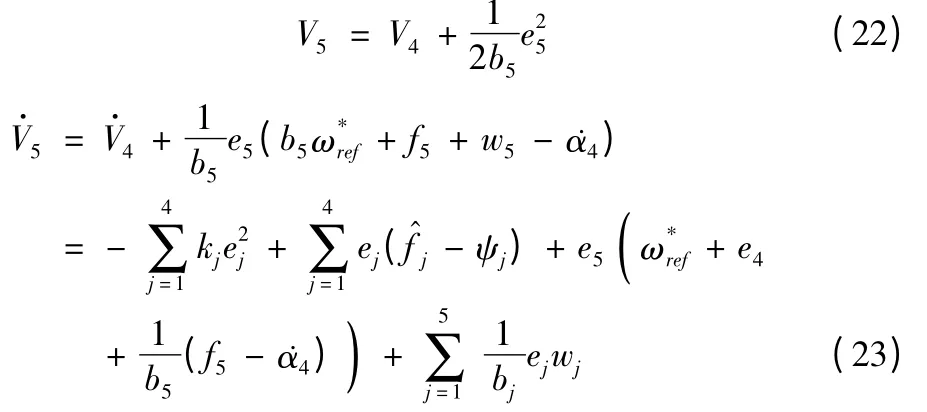
由上式可推导出系统的控制律为:

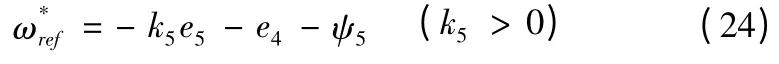
代入(23)式中可得:

采用ψj= ξTθ 逼近未知函数，存在最优逼近向量，对于给定的任意小的常量＞0，|-ξ|≤εj，其中j = 1，2，3，4，5。取=θj，自适应律可设计为:

3 仿真模型分析

在Matlab2010a 中对基于反推法的自适应模糊控制进行仿真实验，系统实验参数设为:

选择模糊集为:

为减少传动机构柔性对伺服机电系统的影响，须压缩速度环带宽。通常交流机电伺服系统速度环带宽在5 到50Hz 之间，为获得优良位置跟踪特性，须将系统速度环带宽设置在20Hz 以内，其伯德图如图1 所示。在此基础上可推出速度控制器参数为:KVP=25，KVI= 24。

选择位置控制器参数为:

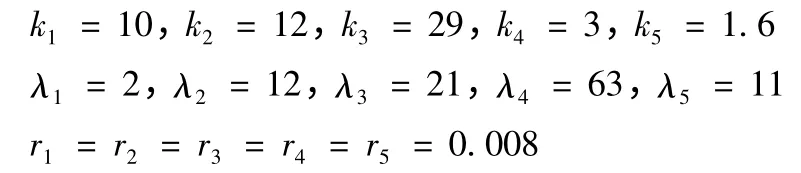
(1)机电参数变化

为检验机电参数发生变化时的控制效果，假设系统参数变化，即转动惯量增加为原来的2 倍，可得响应曲线如图2 所示。从图中可以看出，利用传统反推法时，系统传动响应变化较大，调节时间变长，并有超调。而利用基于反推法的自适应模糊控制时，系统响应改变较小，没有超调的出现。

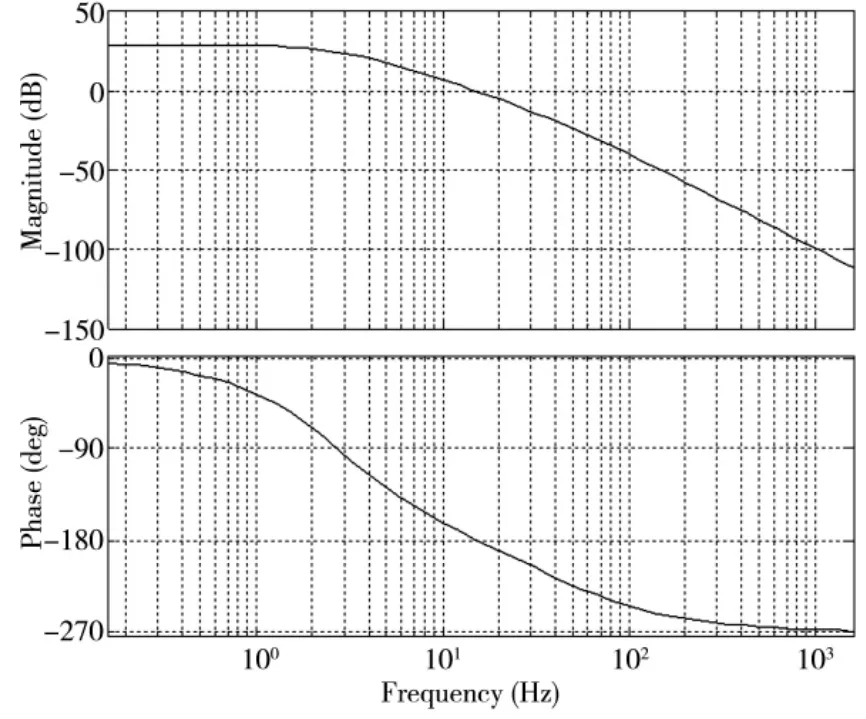
图1 速度闭环伯德图

图2 转动惯量变化2 倍时的响应

(2)伺服位置跟踪分析

为研究伺服传动系统在不同控制方式下的位置跟踪精度及系统参数改变时的特性，假定正弦信号为10sin(0.5t)+10sin(t)，外界干扰折算后为:

从图3 ～图9 中的改变可以推断，基于反推的自适应模糊算法较图中传统反推控制有更好的跟踪精度，误差也比较小，虚拟函数变化比传统反推控制具有更好的动态特性，系统iq电流变化较优。

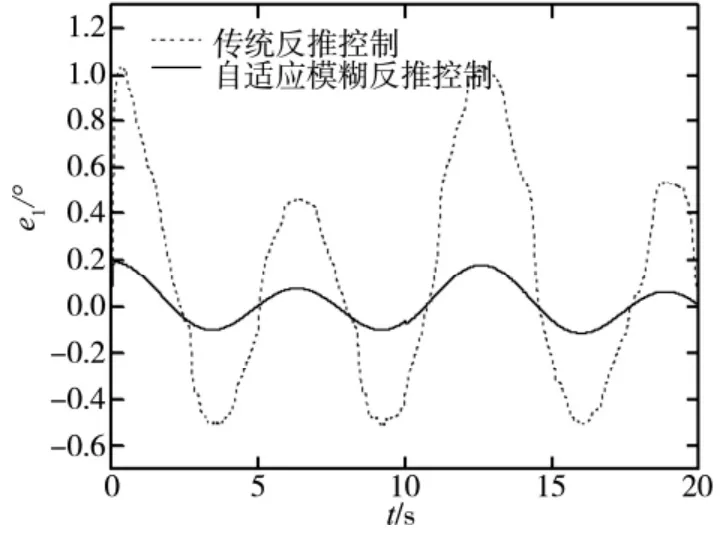
图3 位置误差曲线

图4 虚拟函数α1

图5 虚拟函数α2

图6 虚拟函数α3

图7 虚拟函数α4

图8 传统反推控制iq

图9 自适应模糊反推控制iq

4 结论

本文将自适应模糊反推控制策略引入机电传动系统。依据机电系统模型及李雅普诺夫函数进行了逆向递推，经过了5 步推导构建了位置控制器，利用模糊高斯函数逼近了系统不确定项，理论系统的研究了闭环系统稳定性。为了保证系统的各个状态均为渐进稳定的，在控制率反推过程的每一步中都设有虚拟因子。从仿真实验可以推断出，本文涉及的控制方法与传统反推法相比有更好的系统特性和鲁棒性，虚拟函数的曲线变化较为良好，适用于永磁交流伺服控制系统的机械传动。

［1］陈武晖，毕天姝，杨奇逊，等. 机电耦合对轴系扭振动态特性的影响［J］. 中国电机工程学报，2010，30(4):49－56.

［2］姚延风，刘强，吴文镜. 基于刚柔-机电耦合的机床直线电机进给系统动态性能仿真研究［J］. 振动与冲击，2011，30(1):191－197.

［3］孟杰，陈小安，合烨. 高速电轴电动机-主轴系统的机电耦合动力学建模［J］. 机械工程学报，2007，43(12):160－166.

［4］马艳玲，黄进，张丹. 基于反步自适应控制的伺服系统齿隙补偿［J］. 控制理论与应用，2008，25(6):1090－1094.

［5］袁雷，吴汉松. 船舶航向控制的多滑模鲁棒自适应设计［J］. 控制理论与应用，2010，27(12):1618－1622.

［6］张晋铭，彭辉. 基于DSP 的直流调速系统CMAC 自适应控制［J］. 组合机床与自动化加工技术，2010(8):48－51.

［7］许文斌，桂武鸣，曾全胜. 高速加工伺服进给系统控制研究［J］. 组合机床与自动化加工技术，2010(5):86－89.

［8］Li Y，Tong S. Adaptive fuzzy backstepping output feedback control of nonlinear uncertain systems with unknown virtual control coefficients using MT-filters［J］. Neurocomputing.In Press，Corrected Proof.

［9］Tong S，He X L，Li Y M，et al.Adaptive fuzzy backstepping robust control for uncertain nonlinear systems based on small-gain approach［J］.Fuzzy Sets and Systems，2010，161(6):771－796.

［10］Yu J P，Chen B，Yu H S，et al. Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping［J］. Nonlinear Analysis:Real World Applications，2011，12(1):671－681.

［11］于金鹏，陈兵，于海生，等. 基于自适应模糊反步法的永磁同步电机位置跟踪控制［J］. 控制与决策，2010，25(10):1547－1551.

［12］Tong S C，He X L，Li Y M.Direct adaptive fuzzy backstepping robust control for single input and single output uncertain nonlinear systems using small-gain approach［J］.Information Sciences，2010，180(9):1738－1758.