基于EMC2 的S 形加减速控制算法*

史步海，郭协涛

(华南理工大学 自动化科学与工程学院，广州 510640)

0 引言

数控加工正朝着高速高效方向发展，高速加工要求机床各运动轴能在极短的时间内达到高速运行状态并实现高速准停。目前国内经济型CNC 系统大都采用T 形加减速和指数加减速控制方法，国内外一些高档的数控系统则开始采用S 形加减速控制方法［1］。

EMC2 是开源的CNC 系统软件，自带了T 形加减速控制算法，算法简单，但是启动和结束时存在加速度突变，对机床造成冲击。传统S 形加减速控制算法能较好的克服传统加减速方法的缺点，但算法相对来说比较复杂，实现起来有难度，而且加速度曲线是梯形的，加加速度存在突变。

T 形和传统的S 形加减速控制算法已不能满足高速机床及现代化装备加工的需要，研究新的算法是非常必要的。为使加速度曲线更加平滑，加加速度没有突变，Jianren SUN 等在文献［5］中提出三角函数的平方的正弦曲线加减速算法。为减少s 形加减速控制算法在条件判断和计算方面的复杂性，Shuanghui Hao［3］等提出了等价T 形加减速的概念。本文在对EMC2 各个模块分析的基础上，针对其轨迹规划的原理与加减速控制算法相关程序进行深入的分析，并在此基础上提出了新的改进算法，并将改进后的新型S 形加减速控制应用到其中。

1 EMC2 分析

美国国家标准和技术研究所主持的增强型运动控制器(Enhanced Machine Controller project，EMC)项目是在RTLinux 操作系统上建立的软件数控系统，EMC2 是在原有EMC 软件的基础上加入了许多新的特性和功能。

1.1 软件架构

整个EMC2 软件系统由四个主要模块组成:运动控制器(EMCMOT)运行在实时环境中，执行轨迹规划、正逆运动学运算，计算出电机控制系统的期望输出;I/O 控制器(EMCIO)主要处理紧急启停、冷却装置等其他辅助性输入输出控制;人机界面(GUI)为用户提供友好的操作平台;任务控制器(EMCTASK)是系统枢纽，他从用户界面取得操作信息，然后将其分解为对运动控制器和I/O 控制器的操作，并且监控运动控制器和I/O 控制器完成实际的操作;并且监控运动控制器和I/O 控制器完成实际操作。这种模块化、层次化的软件设计结构使得开发式数控系统易于扩展，模块化的软件架构能够满足各种类型机床的控制［2］。

1.2 运动控制器(EMCMOT)

运动控制器模块是数控系统的核心，主要完成刀具与工件间的相对运动控制，包括对轴位置采样、计算轨迹值、插补以及计算给伺服的输出值等控制。

运动控制器程序完成与伺服控制所有相关工作，其程序位于源码Src/Emc/Motion 中的motion. c。在motion. c 中主要有init_hal_io、函数、init_comm_buffers、init_thread()等函数。init_hal_io 函数初始化HAL 引脚和参数，使得从实时控制模块传来的数据能够接收和使用;init_comm_buffers 函数分配并初始化与EMC 用户空间通讯的命令、状态、和错误信息;函数init_thread()创建实时线程，并在所创建的线程上加载函数，主要创建了Controller 和CommandHandler，其中Controller 线程主要负责轨迹规划和电机伺服控制，CommanHandler 线程用来处理任务层发下来的针对Motion 模块的控制命令。Controller 线程的主要代码位于源码Src/Emc/Motion 下的control. c 中，其中的emcmotController()函数是伺服周期里的主循环函数，所有的状态逻辑计算与轨迹计算都从这里调用。emcmotController()函数依次调用process_inputs()，do_forward()，get_pos_cmd()等函数。其中get_pos_cmd()函数最为重要，用以产生轨迹的位置点。在自由(free)模式下get_pos_cmd()工作在关节空间，每个关节单独规划，每个关节有一个简单的“轨迹规划器”，可实现单轴的点动和回零，其程序直接位于自由模式下对应的程序段中。联动(coordinated)模式下get_pos_cmd()主要调用轨迹规划器(trajectory planer)文件和三次样条曲线文件的函数根据输入(MDI、G 代码)完成笛卡尔空间的直线、圆弧、攻牙插补，可实现多轴的空间运动功能。首先调用tpRuncycle 的得到插补的下个位置坐标存放在emcmotDebug－ ＞queue 队列中，从队列中取出进行逆运动学变换计算得到关节空间各轴坐标存放在positions 里面，则各轴坐标为三次样条曲线的第四点，最后调用cubicInterpolate 函数进行三次样条插补得到各轴新的位置坐标。

位于源码Src/Emc/Kinematics 下轨迹规划器程序文件tc.c 是轨迹点控制器，用以建立和维护轨迹点队列结构体TC_QUEUE_STRUCT，而文件tp. c 是轨迹规划器，主要维护一个大的结构体TP_STRUCT，所有与轨迹规划相关的参数都在里面有所体现，TP_STRUCT 里面的队列为tc.c 里面的轨迹点队列，tp.c主要运算在tpRunCycle()函数中完成。tpRunCycle()中主要是调用tcRuncycle()函数求出当前运行的轨迹段tc 和下一轨迹段nexttc 运行到达的具体位置，tc 和nexttc 都是TC_STRUCT 类型的结构体。有速度融合要求时在tpRunCycle()会计算出融合速度。

运动控制器在EMC2 中被实现成一个在实时周期运行的HAL 模块，提供了6 条线性轴外加3 条旋转轴总共9 轴的控制维度。它周期地执行轨迹规划，计算出下个周期各个运动轴需要执行的位移量，从轨迹规划的方式上，运动控制器模块采取了2 级插补的轨迹规划方式，即粗插补和精插补。粗插补的计算周期通常被配置为精插补的10 倍，主要执行梯形速度轨迹插补。精插补主要负责将精插补的数据通过机器人坐标转换成机器关节空间后，对每个电机轴进行更平滑的3 次样条曲线插补，以控制每个实际电机轴更平滑的运转。

1.3 轨迹规划器工作原理

当EMC2 工作在自由模式下，速度从零开始到零结束，速度以最大加速度增加至速度上限之后以最大速度匀速运行直到开始减速，减速时同样以加速时的加速度进行。这种运动有两种情况:

(1)如果有匀速段，速度加速至期望的进给速度之后进入匀速段，最后减速至0。

(2)如果没有匀速段，速度加速至走完一半的路径，剩下的另一半路径的运动过程中速度减至0。

图1 轨迹规划的位移、速度和加速度

图1 中的位移轨迹表示花了4500 个轨迹规划周期(EMC2 的轨迹规划周期是0.001s)时间刚好走完10 的位移量;速度轨迹表明轨迹规划器的工作原理，首先计算出期望速度(虚线表示)，期望速度要尽可能大而且以最大加速度减速至终点时刚好为0，这样保证了在最短的时间内走完路径，而实际速度(实线表示)受最大速度和最大加速度的限制，一开始从零以最大加速度加速，到达最大速度时以最大速度匀速运行，当实际速度与期望速度相等时，便以最大加速度减速至终点停止运行，这个时间段内期望速度和实际速度的曲线是重叠的;加速度轨迹表示为实际运行过程中的加速度变化，加速度在加速段为最大值，匀速段为0，减速度为反方向的最大值［6］。

图2 轨迹规划速度与实际速度

假设T 为终点位置，P 为当前位置，vs为新的轨迹规划周期中的速度，tm为运行的总时间，am为最大允许加速度，vc为当前速度，ts为轨迹规划周期。

如图2 所示，速度曲线与速度轴和时间轴所围成的面积就是总位移，也就是需要走完的路径长度:

由(1)(2)式有:

创设问题情境能够促使学生积极思考，主动设计或寻找解答方案，从而解决问题。因此，专业课教师在课堂教学中，应当精心创设问题情境，引导学生积极主动地参与课堂学习，参与问题设计、发现、提出、解决的全过程，引导学生在发现和解决实际问题过程中，领悟、总结出发现和解决问题的一般方法、思路与技巧，训练学生解决问题的能力。

由(4)式可解出:

由(2)(5)有:

这等价于EMC2 源码的函数tcRunCycle 中的位移和速度公式。

2 S 形加减速控制算法

传统的S 形加减速控制算法，其基本思想为:将加减速过程细分为7 个阶段:加加速段，匀加速段，减加速段，匀速段，加减速段，匀减速段，减减速段，通过渐变控制各段的加速度使其加减速过程的速度按S 形曲线的形式变化，从而达到减少冲击的目的［4］。为使加速度曲线更加平滑，加加速度没有突变，需对传统的S 形加减速控制算法进行改进。图3为改进后的S 曲线加减速全过程中的位置、速度、加速度以及加加速度曲线。加速过程包含加加速度段、匀加速段、减加速段，减速过程包含加减速段、匀减速段、减减速段;加速和减速之间通过匀速运动衔接，整个过程分为7 段。式中，amax为机床允许的最大加速度;jmax为机床允许的最大加加速度。

图3 改进后的S 形加减速

为减少S 形加减速控制算法在条件判断和计算方面的复杂性，可利用等价T 形加减速的概念，并对S 曲线加速段进行规划。

图4 等价T 形的S 形加减速

S 形加减速控制算法速度曲线的加速段和减速段、加速度曲线的加加速段和减加速段、加速段曲线的加减速段和减减速段分别是对称的，充分利用其对称性可大大简化速度规划过程。S 形加减速控制算法的加速和减速过程的平均加速度为图4 中直线AD 和直线EH 的斜率，所以整个速度曲线可以等价为梯形ADEH 的梯形加减速曲线［2］。

jerk、alim、vlim分别为机床允许的最大加加速度、最大加速度、最大速度，amax、vmax分别为机床实际运行过程中所能达到的最大加速度和最大速度，aequ为规划加减速过程等价加速度，sref为规划路径的长度，s为机床实际需要运行的路径长度。由对称性知:

STEP 1:假设机床实际运行中加加速段amax刚好能达到alim，并且没有匀加减速段和匀速段。

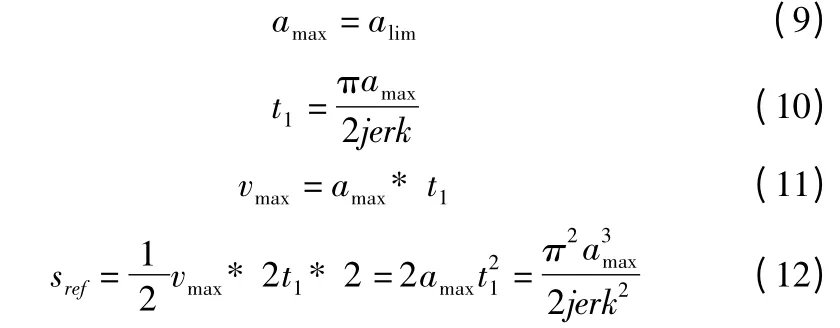
STEP 2:如果s ＜sref，vlim＞vmax，即s 不够大以致加速度没有足够的时间来增大至alim，即amax＜alim，令s=2amax，步骤1 中的amax和vmax需要重新规划。

STEP 3:如果步骤2 中vlim＜ vmax，即vmax超过vlim，amax和vmax需要重新规划，令vmax=amax* t1此时有匀速段。

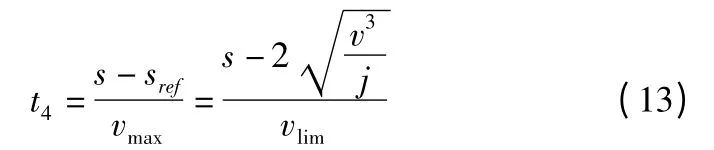
STEP 4:如果s ＞sref，vlim＜vmax，那么步骤1 中的amax和vmax需要重新规划，方法与步骤3 相同，此时有匀速段。

STEP 5:如果s ＞sre，vlim＞vmax，即s 足够长，以致amax有足够的时间来增大至alim，并且vmax没有超过vlim，此时必定产生匀加减速段，假设vmax刚好增大至vlim，重新规划步骤1 中的amax和vmax。

STEP 6:在步骤5 中如果s ＜sref，s 不够长以致vmax无法增大至vlim，重新规划，匀加减速段减小。

STEP 7:在步骤5 中如果s ＞sref，s 足够长以致vmax能够增大至vlim而且产生匀速段，重新规划t2，aeuq，vmax。

图5 改进后的S 形加减速算法规划流程图

3 EMC2 中的运行及测试

EMC2 中采用的插补计算方法是数据采样插补法，也称为时间分割法，它尤其适合于闭环和半闭环以直流或交流电机为执行机构的位置采样控制系统。这种方法是把加工一段直线或圆弧的整段时间细分为许多相等的时间间隔，称为单位时间间隔(或插补周期)。每经过一个单位时间间隔就进行一次插补计算，算出在这一时间间隔内各坐标轴的进给量，边计算，边加工，直至加工终点［2］。

EMC2 本身没有定义S 形加减速中需要用到的最大加加速度这个变量，通过修改源码在配置文件ini 文件中增加最大加加速度的配置，其中单轴的最大加加速度用于自由模式下，全局的轨迹的最大加加速度用于联动模式下。

将完善后的等价T 形的S 形加减速算法应用到EMC2 上，修改相应的源码，在修改后的源文件中编译安装EMC2。在实验平台上的测试结果如下各图所示。

图6 原系统在单轴模式下速度曲线

图7 改造后系统在单轴模式下的速度曲线

图8 原系统在联动模式下的速度曲线

图9 改造后系统在联动模式下的速度曲线

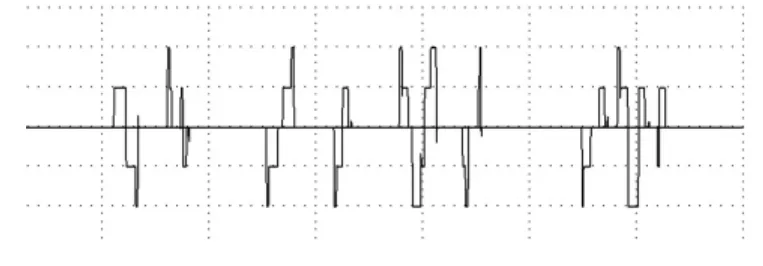
图10 原系统在联动模式下的加速度曲线

图11 改造后系统在联动模式下的加速度曲线

4 结束语

针对EMC2 系统中自带的T 形加减速控制算法启动和结束时存在加速度突变以及传统的S 形加减速控制算法存在加加速度突变的问题，文中通过提出一种新的S 形加减速控制算法，对EMC2 系统主要模块进行改造和升级，并在实验样机平台上进行实际测试。实验证明，机床伺服系统速度和加速度曲线更加平滑，运行稳定，满足高速加工要求的柔性加减速特性，能实现高速启停而又减少对机床的冲击，并且新算法规划简单便于应用。此方法为数控加工的加减速控制提供了一种新的方法和探索。

［1］商允舜. CNC 数控系统加减速控制方法研究与实现［D］. 浙江:浙江大学机械与能源工程学院，2006.

［2］吴晶. 基于EMC2 的工业机器人研究［D］. 广州:华南理工大学自动化科学与工程学院，2011.

［3］Shuanghui Hao，Fang Song，Jie Liu，Minghui Hao.An applied CNC acceleration and deceleration control algorithm research［C］. Proceedings of 2008 IEEE International Conference on Mechatronics and Automation.IEEE，2008:404－407.

［4］石川，赵彤，叶佩青，等. 数控系统S 曲线加减速规划研究［J］. 中国机械工程，2007，18(12):1421－1422.

［5］Tomislav Staroveski，Danko Brezak，Toma udilisk，Dubravko Majetic.Implementation of a Linux-Based CNC open control system.12thInternational Scientific Conference on Production Engineering.Zagreb:Croatian Association of Production Engineering，2009:210－213.

［6］Simple tp notes.http://wiki.linuxcnc.org/cgi-bin/wiki.pl?Simple_Tp_Notes.

［7］Jianren SUN，Chibing HU.Research on simulation of acceleration and deceleration algorithrithm with trigonometric function squared sine shape curve.2010 Third International Conference on Information and Computing.

［8］The EMC Tean.User Manual V2.5.2012.http://www.linuxcnc.org/index.php/English/documentation.

［9］ The EMC Tean. Integrators Manual V2.5.2012. http://www.linuxcnc.org/index.php/English/documentation.

［10］Kim Doang Nguyen，I-Ming Chen，Teck-Chew Ng.Planning algorithms for S-curve Trajectories［J］.IEEE.2007

［11］许军，李华. 开源数控系统EMC2 的编译和启动分析［J］. 现代制造技术与装备，2009，183(6):60.