单位生产成本与加工精度的多工序车削优化*

陈青艳，廖传林，陈 帆

(武汉软件工程职业学院 机械系，武汉 430205)

0 引言

数控加工技术的发展使得切削用量的选择范围和灵活性增大，仅凭传统上的经验或手册选择切削用量已经难以现代市场变化需求，因此运用现代数学优化模型、计算机技术进行切削用量优化选择，对控制和保证加工质量、充分发挥数控车床的能效及企业自身经济效益非常重要。

目前，大部分研究人员非常青睐模拟退火算法(SA/PS)［1］、分 散 搜 索 算 法(SS)［2］、粒 子 群 算 法(PSO)［3］、蚁群算法(ACO)［4］、混合人工蚁群算法(HABC)［5］、混合田径算法(HTHS)［6］用于单位生产成本的多工序车削单目标优化，然而上述算法不仅容易陷于局部最优解，而且只考虑到企业自身的经济效益而忽略了产品加工质量。

近五年来，研究人员为解决上述问题，提出了采用遗传算法及其变形的遗传算法对多工序车削进行多目标优化。如采用进化算法(EA)［7］和遗传算法(GA)［8-9］对刀具耐用度与切削力的车削双目标优化;因非支配排序遗传算法NSGA-II［10］具备精英保留策略、快速非支配排序、排序机制简洁明晰等特点，被广泛应用于车削用量的多目标优化。如采用差分进化算法(DE)与非支配排序遗传算法(NSGAII)［11］对刀具磨损率与金属切除率的多工序车削双目标优化;采用NSGA-II 算法［12］对刀具耐用度、金属切除率与表面粗糙度的多工序车削三目标优化;采用NSGA-II 算法［13］对单位生产率、单位生产成本与表面粗糙度的多工序车削三目标优化;然而上述文献中不仅都没有考虑加工精度对产品加工质量的影响，而且也都没有考虑采用不同变异方法对NSGA-II算法的影响;采用NSGA-II 算法［14］对加工精度与金属切除率的精车切削优化，考虑了精车的加工精度对产品加工质量的影响，然而既没有考虑实际生产中多工序车削情形，又没有考虑生产成本对加工精度的影响。

本文采用高斯变异和多项式变异的NSGA-II 算法，对单位生产成本和加工精度双目标的多工序车削模型进行优化，结合优化实例和切削试验对其有效性进行了详细的数据分析与讨论。

1 多工序车削多目标优化模型

1.1 优化目标函数一

最低单位生产成本使用寿命能保证加工成本最低，即加工一个零件所用的成本最低。

单位生产成本UC($/piece)［15］，可表示:

式(1)中:

式(2)中:

式(1 ～5)中，CM—实际切削费用($/piece);CI—机器闲置的费用($/piece);CR—更换刀具费用($/piece);CT—刀具费用($/piece);dr—粗车背吃刀量(mm);ds—精车背吃刀量(mm);fr—粗车进给量(mm/r);fs—精车进给量(mm/r);Vr—粗车切削速度(m/min);Vs—精车切削速度(m/min);dt—加工余量(mm);n—粗车走刀次数(取整数);kt—切削边缘费用($/min);k0—直接劳动费用与开销($/min);tc—准备装载与卸载辅助时间(min);te—换刀时间(min);h1—刀具移动时间相关系数(min);h2—刀具到达或离开时间相关系数(min);D—工件直径(mm);L—工件长度(mm);C0，p，q，r—刀具耐用度方程常数;Tr—粗车刀具耐用度(min);Ts—精车刀具耐用度(min);Tp—粗车刀具耐用度与精车刀具耐用度的加权组合刀具耐用度(min);θ—加权组合刀具耐用度Tp的加权系数，0≤θ ＜1。

1.2 优化目标函数二

工件加工精度(μm)，可表示成

式(6)中，

式(6－7)中，δg—工件的加工精度(μm);E—材料弹性模量(MPa);J—工件惯性矩(mm4);K—工件装夹方法系数;CFc、xFc、yFc、ηFc、KFc—主切削力系数、背吃刀量指数、进给量指数、切削速度指数、修正系数;η1—背向力与主切削力比值。

1.3 加工约束条件

(1)粗车约束条件

1)刀具耐用度

式中，TL—最小刀具耐用度(min);TU—最大刀具耐用度(min)。

2)切削力约束

式中，k1，μ，ν—切削力方程系数;Fr—粗车切削力(kgf);FU—机床容许的最大切削力(kgf)。

3)切削功率

式中，Pr—粗车切削功率(kW);PU—机床容许最大切削功率(kW)，η—功率效率。

4)稳定切削区域

式中，λ，ν—稳定切削区域相关常数;SC—稳定切削区域限制。

5)切削温度

式中:k2—切削刀具表面温度系数;τ，φ，δ—切削刀具表面温度相关指数;Qr—粗车时切削刀具表面温度(℃);QU—切削刀具表面最大容许温度(℃)。

(2)精车约束条件

1)刀具耐用度

2)切削力

式中，Fs—精车切削力(kgf);

3)切削功率

式中，Ps—精车切削功率(kW)。

4)表面粗糙度

式中，R—刀具圆弧半径(mm);SR、SRU—工件表面粗糙度及所容许的最大表面粗糙度(μm)。

5)稳定切削区域

6)切削表面温度

(3)粗车与精车相互关系约束

式中，k3、k4、k5—粗车与精车参数变量关系常数，k3，k4，k4≥1;

(4)参数变量取值范围约束

1)粗车切削速度

式中，VrL—最小粗车切削速度(m/min);VrU—最大粗车切削速度(m/min)。

式(22)中，

nmax，nmin分别为机床允许的最大转速与最小转速;

2)粗车进给量

式中，frL—最小粗车进给量(mm/r);frU—最大粗车进给量(mm/r)。

3)粗车背吃刀量

式中，drL—最小粗车背吃刀量(mm);drU—最大粗车背吃刀量(mm)。

4)精车切削速度

式中，VrL—最小精车切削速度(m/min);VrU—最大精车切削速度(m/min)。

式(27)中:

5)精车进给量

式中，frL—最小精车进给量(mm/r);frU—最大精车进给量(mm/r)。

6)精车背吃刀量

式中，drL—最小精车背吃刀量(mm);drU—最大精车背吃刀量(mm)。

7)粗车走刀次数约束

简化成:

因此:

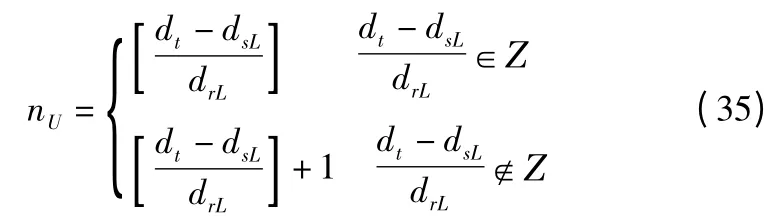
式中，nL，nU—分别为粗车走刀次数最小值与最大值，Ζ—为整数集，［·］为取整函数;

2 NSGA-II 遗传算法

2.1 算法流程

步骤一:设置种群规模N，最大遗传代数maxGen，其中N =20 ～200，最大遗传代数maxGen =100 ～5000。

设置以单位生产成本UC 最小化与加工精度δg最小化为优化目标，目标函数［15］表达:

步骤二:设置种群个体结构体的组成;

为了减少编码误差，采用实数编码，用结构体来表示。个体结构体组成元素:粗车切削速度、粗车进给量、精车背吃刀量、精车切削速度、精车进给量五个变量，单位生产成本UC、加工精度δg优化目标函数及其约束条件。

步骤三:对含有N 个体的种群规模进行初始化，首先在变量取值范围内随机分配变量值，然后分别计算两目标函数值及约束条件的取值，最后对N 个体进行非支配排序，得到初始种群P0。

步骤四:遗传代数t=1。

步骤五:判断条件遗传代数t≤maxGen，若不满足，则转向步骤十四。

步骤六:对遗传代数t 的种群Pt进行选择、交叉和变异，产生子代种群Qt。

步骤七:合并种群，Rt=Pt∪Qt，新种群Rt的规模为2N。

步骤八:对新种群Rt进行非支配等级排序，得到非支配等级分类不同的前沿集合F，式中F =(F1、F2、…)。

步骤九:令遗传代数t+1 种群Pt+1=Φ，i=1。

步骤十:判断条件|Pt+1| + |Fi|≤N，若不满足条件，则转向步骤十三。

步骤十一:对第i 前沿集合Fi进行拥挤距离计算，并按拥挤距离降序排列，Pt+1=Pt+1∪Fi，i =i +1，转向步骤十。

步骤十二:对第i 前沿集合Fi进行拥挤距离计算，并按拥挤距离降序排列，选择集合Fi中前N－|Pt+1|个元素，得到t +1 代种群Pt+1=Pt+1∪Fi［1:(N－ |Pi+1|)］。

步骤十三:对t+1 代种群Pt+1进行选择、交叉和变异，产生子代种群Qt+1，t=t+1，转向步骤五。

步骤十四:得到不同遗传代数t 的单位生产成本UC 与加工精度δg的Pareot 最优集合即对应参数取值集合，1≤t≤maxGen。

2.2 NSGA-II 算法优化

2.2.1 对约束条件的处理方法

解i 支配解j，如果满足下述条件之一:

(1)解i 可行，而解j 不可行。

(2)解i 与解j 都不可行，但解i 有更小的整体约束违反。

(3)解i 与解j 都可行，解i 支配解j。

2.2.2 NSGA-II 算法的选择、交叉与变异

选择方法:采用拥挤距离非支配排序选择算符;

交叉方法:中间重组交叉［来自GADS 工具箱(MATLAB2011a 版)］(参数:比率Ratio)。

变异:高斯变异［来自GADS 工具箱(MATLAB2011a 版)］(参数:扩张因子Scale、收缩因子Shrink)及多项式变异［16］。

为讨论和描述方便，将采用高斯变异方法的NSGA-II 命名为GNSGA-II，而将采用多项式变异方法的NSGA-II 算法命名为PNSGA-II。

3 实例分析

3.1 实例参数

工件材料45 钢锻件，工件长度300mm，工件直105MPa;主切削力系数2650、其背吃刀量指数1.0、径50mm，装夹方法系数3，材料弹性模量2.2 ×进给量指数0.75、切削速度指数－0.15、主切削力修正系数0.8。。

机床采用CAK6136V，主电机功率:5.5kW;功率效率:0.8，最大允许主切削力:5000N;主轴转速范围:200 ～3000 r/min;纵向进给量范围:0.05 ～1.12mm/r;背吃刀量范围:0.05 ～5mm，表面粗糙度1.6μm。

其余参数完全来自文献［2］，具体如下:

3.2 实例数据计算与验证

GNSGA-II 算法具体参数设置:种群规模N=100，遗传代数maxGen =10000，交叉概率0.4，变异概率0.4，中间重组交叉参数:比率Ratio =1.2;高斯变异参数:扩张因子Scale=0.1，收缩因子Shrink=0.5。

PNSGA-II 算法具体参数设置:种群规模N =100，最大遗传代数maxGen =10000，交叉概率0.4，变异概率0.4，中间重组交叉参数:比率Ratio =1.2，多项式变异参数:变异分布系数ηm=20。为讨论方便，取加权组合刀具耐用度Tp的加权系数θ=0.5。

比较粗车走刀次数n=2 时，分别采用GNSGA-II、PNSGA-II 计算得到的结果。分别采用高斯变异GNSGA-II 算法与多项式变异PNSGA-II 算法对单位生产成本和加工精度的多工序车削模型进行优化，如图1a所示，遗传代数gen≥2000 时，单位生产成本与加工精度的Pareto 最优解集个数均≥99，占种群规模N 的99%以上。图1a 同时也表明，要想获得低的单位生产成本，必须以牺牲加工精度为代价;同样的，要想获得高的加工精度，要增加所花费的单位生产成本;换句话说，加工精度与单位生产成本是相互矛盾的。采用高斯变异GNSGA-II 算法，遗传代数gen =5000 时，单位生产成本与加工精度的Pareto 最优解集仍未收敛到稳定的Pareto 最优解集，如图1b 所示。

图1a 为Pareto 最优解集个数演化过程;图1b、c为遗传代数Gen =2000、5000、9000、10000;图1d 为遗传代数Gen =10000 时单位生产成本与加工精度的Pareto 最优解集。

而采用多项式变异PNSGA-II 算法，遗传代数gen=2000 时，单位生产成本与加工精度的Pareto 最优解集已经收敛到稳定的Pareto 最优解集，如图1c 所示。

采用高斯变异GNSGA-II 算法所获得的Pareto最优解集位于采用多项式变异PNSGA-II 算法得到的Pareto 最优解集上方，如图1d 所示，表明采用多项式变异PNSGA-II 算法得到的单位生产成本与加工精度Pareto 最优解集优于采用高斯变异GNSGA-II算法得到的单位生产成本与加工精度Pareto 最优解集。下面采用PNSGA-II 算法进一步计算粗车走刀次数不同取值的情形，最大遗传代数maxgen=2000。

图1 单位生产成本与加工精度Pareto 最优解集

粗车走刀次数n=1 时，得到Pareto 最优解集中的所有加工精度均＞30μm，如图2 所示，不符合IT7的加工精度要求;因此，要想获得IT7 加工精度时的生产成本，粗车走刀次数须n≥2。

图2 生产成本与加工精度Pareto 最优解集(n=1)

比较图1、图3、图4，粗车走刀次数n 分别2、3、4时，得到的Pareto 最优解集的加工精度均满足IT7 要求，显然，相同加工精度下，粗车走刀次数n =2 时，单位生产成本最小。如加工精度4μm 时，粗车走刀次数n 分别2、3、4 时，单位生产成本依次2.329 $、2.783 $、3.239 $。

图3 生产成本与加工精度的Pareto 最优解集(n=3)

图4 生产成本与加工精度的Pareto 最优解集(n=4)

CAK6136V 的加工精度可达IT6、IT7，在实际加工中，为满足约束条件，数控加工编程时输入参数依次为:粗车背吃刀量2.975mm，粗车进给量1.112mm/r，粗车切削速度86.796m/min;精车背吃刀量0.05mm，精车进给量0.121mm/r，精车切削速度359.051m/min。此时数控加工得到的工件加工精度约3.981μm，单位生产成本为2.332 $(生产成本核算参照文献［2］)，与计算结果接近，表明NSGA-II 算法用于单位生产成本和加工精度的多工序车削双目标优化是有效的。

4 结论

通过不同变异方法的NSGA-II 算法，对生产成本与加工精度的双目标优化，得到如下结论:

采用多项式变异方法的NSGA-II 算法，比高斯变异方法的NSGA-II 算法更快更好地收敛到Pareto最优解集;

实例数据仿真及实验验证，采用多项式变异方法的NSGA-II 算法得到的生产成本与加工精度Pareto 最优解集是有效的;

优化实例与切削试验表明，粗车走刀次数一次往往无法满足加工精度的需求。为了首先满足加工精度的需求，首先确定较低的精车背吃刀量(如0.05mm);然后根据精车背吃刀量，计算粗车走刀次数n 最小时的粗车背吃刀量，切削实例中粗车走刀次数最小n=2;这样六变量的问题就转变为四变量的问题，加快获得优化结果。

［1］M. C. CHEN and D. M. TSAI，A simulated annealing approach for optimization of multi-pass turning operations［J］，INT. J. PROD. RES，1996，34(10):2803－2825.

［2］ M. C. CHEN，Optimization machining economics models of turning operations using the scatter search approach［J］，International Journal of Production Research，2004，42:2611－2625.

［3］A.R. Yildiz，A novel particle swarm optimization approach for product design and manufacturing ［J］，International Journal of Advanced Manufacturing Technology，2009，40(5):617－628.

［4］Yi-Chi Wang，A note on‘Optimization of multi-pass turning operations using ant colony system’［J］，International Journal of Machine Tools ＆ Manufacture，47(2007):2057－2059.

［5］A. R. Yildiz，A new hybrid artificial bee colony-based approach for optimization of multi-pass turning operations［J］，Information Science. 9644(2012)1－9.

［6］A.R.Yildiz，Hybrid Taguchi-Harmony Search Algorithm for solving engineering optimization problem［J］，International Journal of industrial engineering theory，Applications and practice，2008，15(3):286－293.

［7］Rituparna Datta and Anima Majumder. Optimization of turning process parameters using multi-objective evolutionary algorithm［J］. IEEE，2010.

［8］陈青艳. 非支配排序自适应遗传算法的车削优化［J］.机械设计与研究，2013(2):97－101.

［9］Ramon Quiza Sardinas，Marcelino Rivas Santana，Eleno Alfonso Brindis，Genetic algorithm based multi-objective optimization of cutting parameters in turning processes［J］，Apllications of Artificial Intelligence，19(2006):127－133.

［10］Kalyanmoy Deb，Amrit Pratap. A Fast and Elitist Multi-objective Genetic Algorithm:NSGA-II［J］. IEEE Transactions on Evolutionary Compution，2002，6(2):182－197.

［11］S.H.Yang，U.Natarjan，Multi-objective optimization of cutting parameters in turning process using differential evolution and non-dominated sorting genetic algorithm-II approaches［J］，Int.J.Adv.Manuf. Technol. 2009，49:773－784.

［12］Jianling Chen，Multi-objective Optimization of Cutting Parameters with Improved NSGA-II［J］，2009.

［13］Rituparna Datta，Kalyanmoy Deb，A Classical-cum-Evolutionary Multi-Objective Optimization for Optimal Machining Parameters［J］，World Congress on Nature ＆ Biologically Inspired Computing，2009:607－612.

［14］陈青艳，胡成龙，杜军. 加工精度和金属切除率的精车切削优化［J］. 组合机床与自动化加工技术，2013(3):111－114.

［15］Y.C.SHIN and Y.S.JOO. Optimization of machining conditions with practical constraints［J］. INT. J. PROD.RES.，1992，30(12):2907－2919.

［16］M.M. Raghuwanshi and O. G. Kakde，Survey on multiobjective evolutionary and real coded genetic algorithms［J］，Proceedings of the 8th Asia Pacific Symposium on Intelligent and Evolutionary Systems，2004:150－161.