径向基函数神经网络在高速铣削表面粗糙度预测中的应用*
陈英俊,陈庆华
(肇庆学院 电子信息与机电工程学院,广东 肇庆 526061)
近年来,随着高速切削技术飞速发展,对高速切削加工技术的研究越来越深入;同时随着对机械产品性能、寿命和可靠性要求的不断提高,对零件已加工表面粗糙度也提出了更高的要求。影响表面粗糙度的因素很多,其中切削用量的选取是主要因素。由于高速切削表面粗糙度的形成机理还不成熟,对切削参数的选用还没有成熟的经验公式、数据可供参考[1-3]。因而,通过实验研究高速切削表面粗糙度与工艺参数的关系,建立精度和可靠性均较高的表面粗糙度预测模型具有重要的现实意义,它不仅可以解决工艺参数优化问题,还能精确有效地保证加工质量。
目前,对高速切削表面粗糙度建模及参数优化的方法较多,常见的有响应曲面法、遗传算法及BP 神经网络等,但各种方法均有优缺点[4-6]:响应曲面法结合多元线性回归所需样本数量少,但在建模精度和泛化能力方面往往不能满足要求;BP 神经网络在处理非线性模式识别方面表现出很好的特性,但BP 算法收敛速度慢,误差函数在学习阶段可能会陷入局部极小值;虽然遗传算法可以避免局部极小,但一般都需要巨大的计算量。作为人工神经网络的一个重要分支,近期发展起来的径向基函数(Radial Basis Function,RBF)神经网络较为有效地解决了上述问题,学习速度比通常的BP 算法快得多,但在高速铣削加工领域的应用还是一片空白。基于此,本文应用RBF 神经网络建立数控高速铣削表面粗糙度预测模型,并对其精度进行了验证,从而可对高速铣削工艺参数进行优化和决策。
1 RBF 模型及其算法实现
1.1 RBF 模型结构
RBF 神经网络,即径向基函数网络是一种三层前向式网络,由一个输入层、一个隐含层和一个输出层组成,如图1 所示。RBF 网络不仅具有任意精度的泛函逼近能力和最优泛函逼近特性,而且具有较快的收敛速度,已被广泛应用于函数逼近、信号处理、系统建模和预测控制等领域。本文选用Gaussian函数作为RBF 神经元,表达式如下[6-7]:

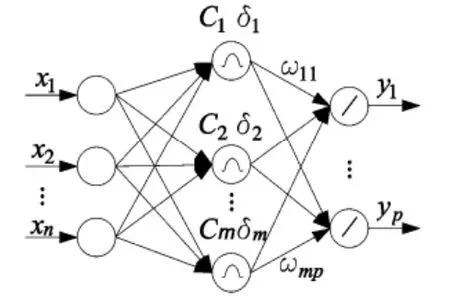
图1 RBF 神经网络简图
此时,输出层神经元的输出为:
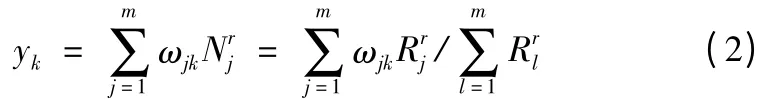
式中,yk为输出层第k 个神经元的输出;为隐层第j 个RBF 的归一化输出;ωjk为隐层至输出层的连接权值;m 为隐层RBF 节点数。
1.2 RBF 模型的学习算法
RBF 模型的结构参数需通过学习来确定。本文选用K-均值聚类算法来确定RBF 的中心Cj和宽度δj,采用误差梯度下降法训练隐层至输出层的权值ωjk。参考相应文献,具体学习过程如下[5,7]:
(1)确定隐层RBF 的中心Cj:

重复以上过程,直至所有聚类中心Cj不再变化,最后将Cj赋给隐层各单元作为RBF 中心。
(2)确定RBF 的宽度δj
RBF 宽度δj为与每个RBF 中心相联系的聚类域中样本散布的一个测度值,可表示为:

(3)确定从隐层到输出层的连接权值ωjk
令输出层输出yk的期望值为Tk,定义网络的目标函数为其全局误差E:
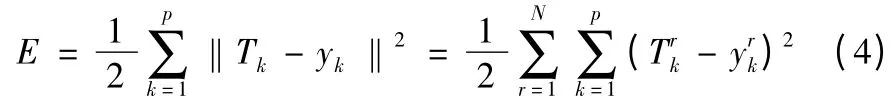
在基函数结构参数Cj、δj确定后,(4)式即为ωjk的函数,采用误差梯度下降法训练权值ωjk,使全局误差E 小于预先设定的精度值。
2 高速铣削表面粗糙度预测模型的建立
2.1 输入变量的确定
输入变量选择是神经网络建模前的一项重要工作,能否选出最能反映期望输出变化原因的输入变量,直接关系到网络预测的性能。在高速铣削加工中,切削用量是影响表面粗糙度值的重要因素,主要包含:铣削速度vc(或主轴转速)、每齿进给量fz(或进给速度)、铣削深度ap和铣削宽度ae,因而,建模前选取这四个工艺参数作为输入变量。
2.2 试验样本选取
为减少试验次数,提高预测模型的准确性,需要合理设计试验方案才能达到预期的目的。本文以相关文献试验数据为样本[8],为表面粗糙度预报分析作准备。该试验在立式高速加工中心上进行,加工工件为模具型腔,加工方式为端面高速铣削。每次铣削试验后采用SE-3H 型表面粗糙度仪测量试样表面粗糙度值,样本数据如表1 所示。
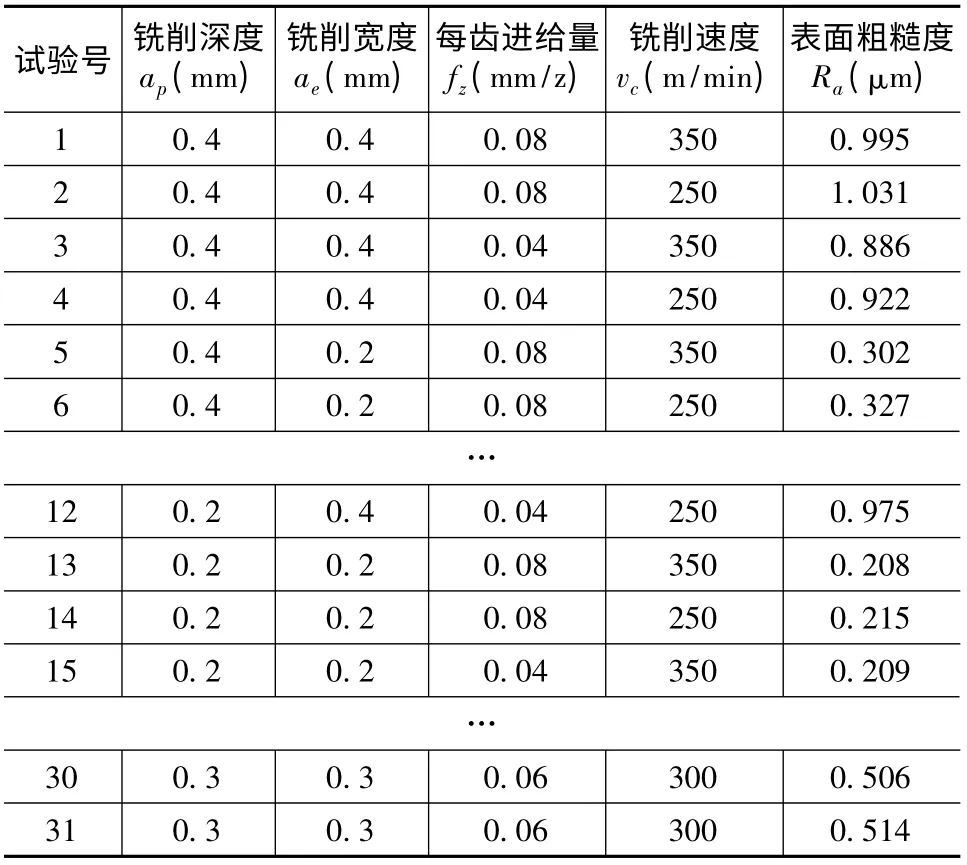
表1 高速铣削加工样本数据
2.3 样本归一化处理
由于各铣削参数的取值范围和量纲不同,为了在同一标准下确定各参数对表面粗糙度的影响,方便对RBF 神经网络进行学习训练,必须先对输入输出数据进行归一化(或标准化)处理:
将输入输出数据变换为[0,1]区间的值。常采用如下变换式:

式中:~x 为相应输入、输出的归一化结果,x 为相应输入、输出值,xmax和xmin为相应输入、输出的最大值及最小值。
2.4 模型的预测性能
采用图1 所示的RBF 网络结构,建立输入变量分别为铣削速度、每齿进给量、铣削深度和铣削宽度,而输出变量为表面粗糙度的预测模型,RBF 网络隐层神经元数目依据样本特性以及要求的预测精度动态确定。
选取24 组经归一化后的数据进行学习和建模。图2 为RBF 神经网络的训练过程,可见,经过11 次学习过程(即采用了11 个RBF 神经元),输出误差就能满足精度要求。

图2 RBF 神经网络的训练过程
选用剩下的样本数据对该模型进行精度检验,将模型的预测结果与表面粗糙度实测值进行比较,其结果如图3 所示。

图3 RBF 模型预测值与表面粗糙度实测值的比较
可见,表面粗糙度预测值与实测值非常接近,说明采用RBF 神经网络方法建立的预测模型,能够较准确地预测高速铣削的表面粗糙度,从而能实现对高速铣削已加工表面质量的稳定控制。
将RBF 神经网络模型的预测结果与常用的多项式回归模型进行比较。对样本数据进行多项式回归拟合以建立回归模型[8],与RBF 模型的精度对比如表2 所示。

表2 两种模型预测精度的比较
表2 中,相对误差(%)定义为:[(预测值实测值)/实测值]×100%。需要提及的是,RBF 模型的预测精度需建立在大样本训练的基础上,尽管可利用样本数据较少,无法使该模型达到较佳的性能,但从表2 中可看出,RBF 模型的预测精度稍高于多项式回归模型,达到满意的精度要求。随着训练样本数据的增多,RBF 模型的预测精度将会进一步提高。
3 高速铣削表面粗糙度的预报分析
预测模型的重要作用体现在对加工质量的监测和控制,以及对工艺参数的优化指导。在这里,利用所建立的RBF 预测模型对高速铣削模具型腔时表面粗糙度进行预报分析,结果如图4 所示。可见,RBF 模型预测的工艺参数的影响规律与相应文献回归分析的结果相一致[8]。铣削工艺参数对已加工表面粗糙度的影响呈非线性关系,且各工艺参数的影响程度及趋势并不相同。表面粗糙度Ra随vc的增大而减小,随fz、ap和ae的增大而增大;同时,铣削宽度ae的影响相当显著。预报分析结果表明,采用RBF 模型在对高速铣削表面粗糙度预报的基础上对加工参数进行分析优化是可行的,既降低了试验成本,并能满足实际工程需要。此外,通过合理选择工艺参数,尤其在控制铣削深度和铣削宽度的情况下,可获得Ra0.3μm 以下的已加工表面粗糙度。

图4 已加工表面粗糙度预报分析
4 结论
(1)采用RBF 神经网络方法建立了高速铣削已加工表面粗糙度的预测模型。预测值与实测值非常接近,且预测精度略高于回归模型的精度,说明该预测模型对高速铣削已加工表面质量的控制具有指导意义。
(2)运用预测模型对表面粗糙度进行了预报,并分析了工艺参数的影响规律,验证了模型对质量监测及工艺参数优化的可行性及实用性。结果表明:高速铣削模具型腔时,表面粗糙度Ra随vc的增大而减小,随fz、ap和ae的增大而增大,通过合理选择工艺参数,尤其在控制切削深度和切削宽度的情况下,可获得Ra0.3μm 以下的已加工表面粗糙度。
[1]Hamdan Ahmad et.al.,An optimization method of the machining parameters in high-speed machining of stainless steel using coated carbide tool for best surface finish,International Journal of Advanced Manufacturing Technology,2012,58(1-4):81-91.
[2]Cui XB,Zhao J,Surface roughness and chip formation in high-speed face milling AISI H13 steel,NATIONAL JOURNAL OF ADVANCED MANUFACTURING TECHNOLOGY,2012,61(1-4):1-13.
[3]陈锦江,龙超,等. 高速铣削P20 模具钢表面粗糙度预测模型研究[J]. 组合机床与自动化加工技术,2012(12):60-62.
[4]袁人炜,陈明,等. 响应曲面法预测铣削力模型及影响因素的分析[J]. 上海交通大学学报,2011,35:1041-1044.
[5]高印寒,唐荣江,等. 基于径向基函数神经网络的车内噪声品质评价系统[J]. 吉林大学学报(工学版),2012(6):1378-1383.
[6]吴艳华,张永强,等. 径向基神经网络在三维激光切割中的应用[J]. 中国机械工程,2006(12):1234-1237.
[7]韩立发,等. 径向基函数神经网络在复合材料滚压加工中的应用[J]. 组合机床与自动化加工技术,2005(4):8-10.
[8]刘永云,孙传俊,马日光. 高速精加工表面粗糙度值预测模型研究[J]. 模具制造,2007(12):63-66.

