板式行星分度凸轮机构的动力学和强度分析

关 伟，田广才，王 敏

(1.西安启源机电装备股份有限公司研发中心，西安 710018;2.军事交通学院 军事物流系，天津300161)

环板式行星分度凸轮机构是一种新型的凸轮型间歇机构，具有结构简单、分度数大、承载能力强、体积小、无输出机构等优点［1］。以机构学的观点分析，环板式行星分度凸轮机构是平行四边形机构和凸轮机构的串联组合［2-4］，其组成原理如图1 所示。

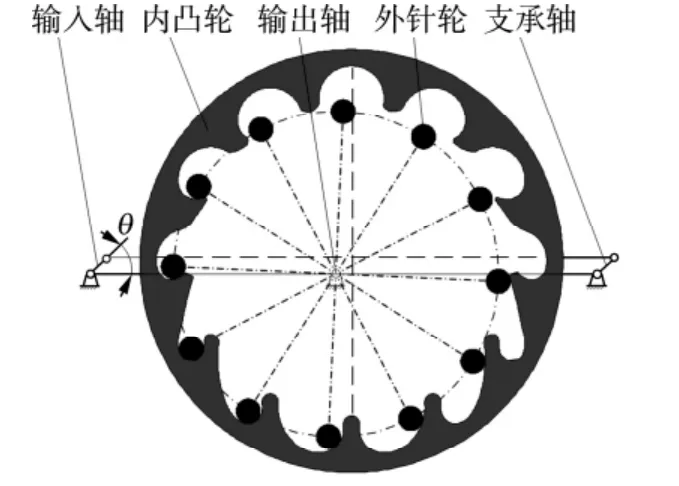
图1 传动原理图

图示的平行四边形机构中，有动力输入的曲柄轴称为输入轴，无动力输入的曲柄轴称为支承轴。平行四边形机构的连杆称为内凸轮环板，其上制有内凸轮，与输出轴上的外针轮组成凸轮——针轮啮合副。当输入轴逆时针等速回转时，带动内凸轮环板做平动，通过凸轮——针轮副推动输出轴做顺时针间歇回转，其运动规律可由具体应用场合确定［5］。

1 动力学分析

1.1 SolidWorks 模型

利用SolidWorks2010 建立环板式行星分度凸轮机构三维模型，见图2。为便于观察，对其上箱体作消隐处理。

1.2 Motion 运算结果

SolidWorks2010 的“Motion 分析”模块加载约束，例如旋转、平行等，输入轴转数20RPM，输出轴加载200NM 的反向转矩，凸轮和针齿的材料为45 号钢，如图3 所示，保留主要运动部件，其他作固定消隐。

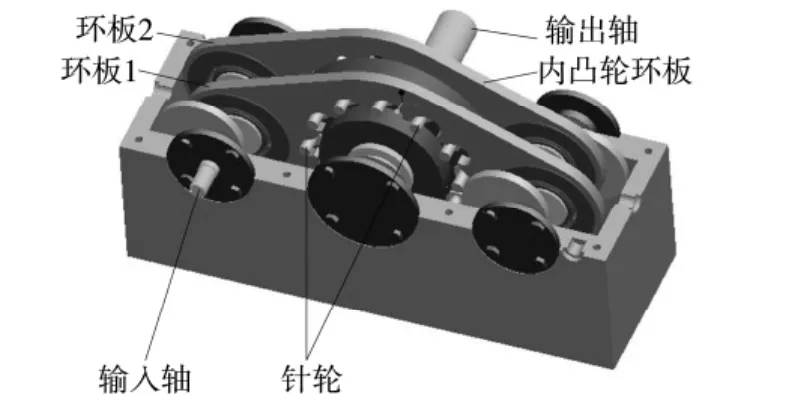
图2 实体模型

图3 Motion 分析模型

Motion 分析计算可以得到输出轴转速如图4 所示，针齿与两个环板的接触力如图5 和图6 所示。

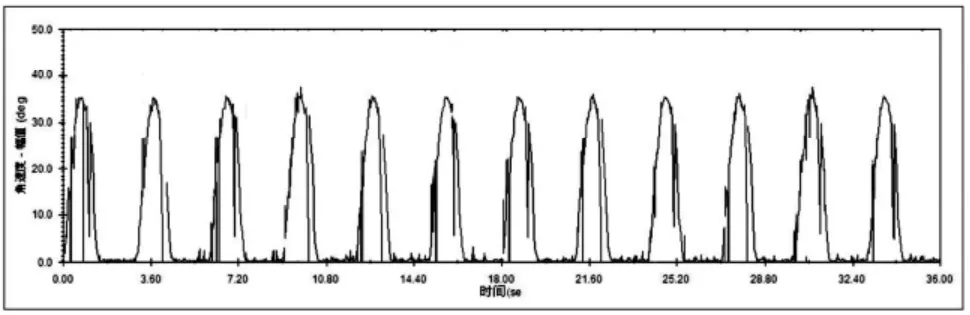
图4 输出轴的转速

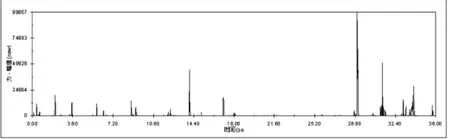
图5 针齿与环板1 的接触力

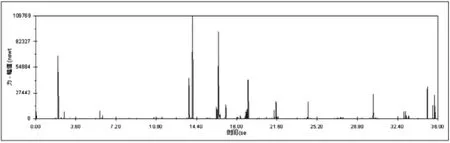
图6 针齿与环板2 的接触力

从图4 可以看出，输出转速符合预计的正弦函数关系;从图5 和图6 得出，在设计针齿时，其承载能力要满足11 万牛顿的力。

2 强度分析

强度分析是凸轮机构设计的基础。环板式行星分度凸轮机构是多齿啮合传动，属于超静定问题，针齿与凸轮之间的受力状态十分复杂，凸轮针轮副的受力状况是整个机构受力分析的关键，即强度校核的难点。

通过强度分析可以为零部件尺寸设计提供依据。针对环板式行星分度凸轮机构的强度分析，已有部分学者进行了探索和研究，陈新动等［6］在介绍该凸轮机构传动原理的基础上阐述了整机的摆动力以及摆动力矩的平衡问题。刘明涛［7］在进行机构的受力分析时，假设啮合副的装配间隙为零并忽略了摩擦因素，且将内凸轮视为刚体，忽略凸轮的变形，由于存在上述一系列的假设，使得所建的模型与实际情况有所出入，故这里将借助ANSYS 软件，建立考虑尽可能多影响因素的环板式行星分度凸轮机构的平面接触模型，精确计算其受力及应力/应变分布情况。

2.1 有限元模型的建立

2.1.1 凸轮阔线的建立

根据共轭齿形的形成原理，按照所设想的传动过程即:凸轮随平行四边形机构做沿逆时针方向旋转的平动，针轮沿顺时针方向做间歇运动，用矢量函数法可以得到凸轮的理论阔线。凸轮的实际阔线是以理论阔线为中心，以针轮的半径为半径形成的包络线，即内、外等距曲线拼接而成的，可用内、外等距曲线所围区域的布尔运算来求解，然后对尖点进行修缘，即得到凸轮的实际阔线(如图1 所示)，其中凸轮廓线的设计参数见表1。

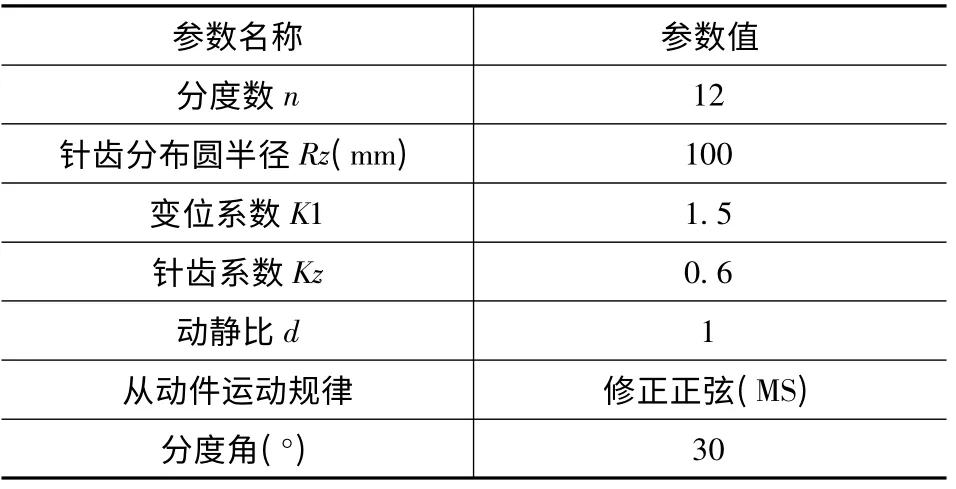
表1 机构设计参数表

2.1.2 有限元模型的建立

由于凸轮阔线非常复杂，所以采用自底向上的方法建模。首先由计算强大的Matlab 软件求得凸轮阔线上二千四百个点的点阵坐标，设制输出ANSYS承认的点阵坐标格式，进而编写ANSYS 软件的APDL 程序建模。

环板式行星分度凸轮机构的凸轮和针齿的材料参数和单元选择如表2 所示。

表2 材料特性和单元类型

网格划分是建模中非常重要的一个环节，网格划分的好坏直接影响计算精度与计算效率。根据此凸轮机构的特殊性，凸轮和针轮啮合过程中，与凸轮接触的针齿个数是变化的，有八到十一个。所以接触区域的网格细化，如图7 所示。这样不仅接触区域符合计算要求，而且非接触区域节省了计算时间。

图7 接触区域细化的网格

环板式行星分度凸轮机构的平面接触模型的网格划分如图8 所示，对不同的分析位置，有限元模型的单元数和节点数有所差别，其平均单元数为25000，平均节点数为50000。

图8 凸轮和针齿的网格划分

2.1.3 识别接触对

通过目标单元和接触单元来定义模型在变形期间可能发生接触的区域。原则:在能保证足以描述所需要的接触行为的条件下，尽量定义更小的局部化接触区域，以更有效地进行计算。所以明显看出凸轮和针齿不接触的，直接不设接触对;接触不易判断的或凸轮在载荷作用下可能接触的进行接触设置。通过图9 计算结果可以判断已设置的接触对中有两对实际不接触。

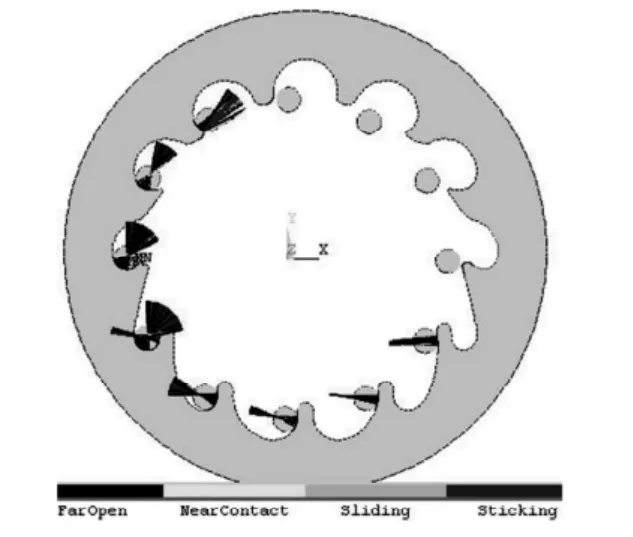
图9 接触状态

针轮作为目标面，凸轮作为接触面。目标面采用单元TARGE169，接触面采用单元CONTA172。设置单元关键字:单位时间步长设置选择自动二等分;初始穿透或缝隙的影响为包括由用户指定的接触表面便宜量，排除由初始几何形状引起的缝隙或穿透。将实常数穿透容差因子和初始靠近因子分别为0.5 和－2mm。

2.1.4 设置边界条件和载荷

约束针轮:限制针齿圆心和附近节点的水平和垂直方向的移动，这样针齿在受到接触力下既不会移动也不会转动。

约束凸轮:限制凸轮最外一圈所有节点在“径向”方向的移动，这样凸轮在力的作用下只能旋转，不会移动。

施加载荷:对凸轮最外一圈的节点施加周向力，即对凸轮施加转矩载荷。

2.1.5 定义求解选项和载荷步求解

指定分析类型为静态分析。使用牛顿拉普森平衡迭代的算法，使在每个载荷增量的末端解达到平衡收敛。

2.2 有限元结果分析

为了模拟机构运行过程中凸轮与针齿的接触情况，将机构输入转角的一个运动周期离散成36 等分，即对每隔10°的36 个离散位置分别进行接触计算。考虑到输入转角为180° ～360°时机构处于停歇期，其惯性负荷为零，故不对其进行计算。

经过计算可以得到凸轮与针齿接触的18 位置的应力云图，由于篇幅限制这里仅列出其中6 个位置，如图10 所示。

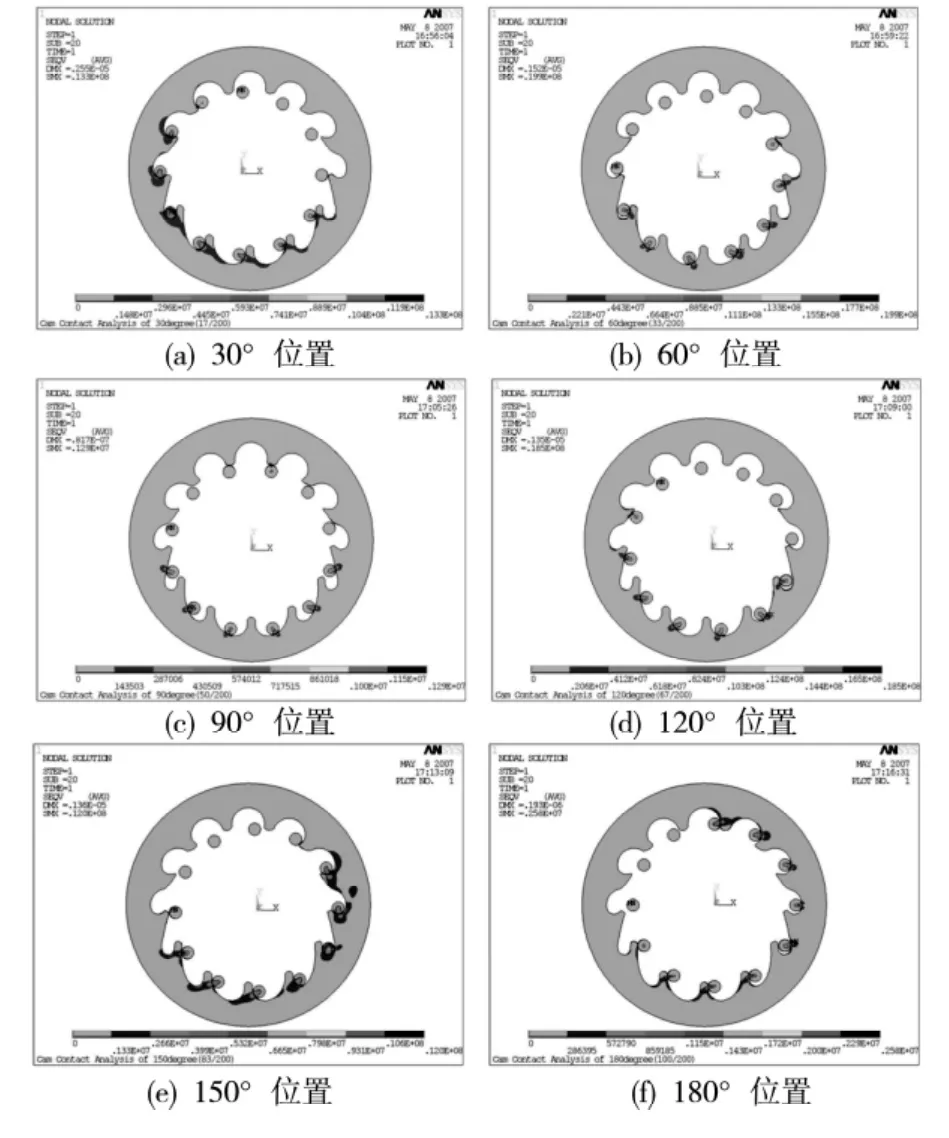
图10 机构在分度期的应力云图

从图10 可以看出，上述各离散位置的接触应力云图具有一个共同的规律:凸轮——针轮啮合区附近的应力值较大，而在非啮合区域，尤其是远离啮合点的凸轮外缘处，其应力值甚小，近似为零。换言之，环板式行星分度凸轮机构在工作载荷作用下，只有在接近啮合区的局部产生明显的变形。

在环板式行星分度凸轮机构中，外载荷主要是机构从动件和后置执行机构的惯性负荷。外载荷按照修正正弦的规律变化，当输入转角为25.2°时外载荷最大，其值为145Nm。经分析可得外载荷最大位置处机构的应力云图，如图11 所示。由图可知最大应力为11.3Mpa。

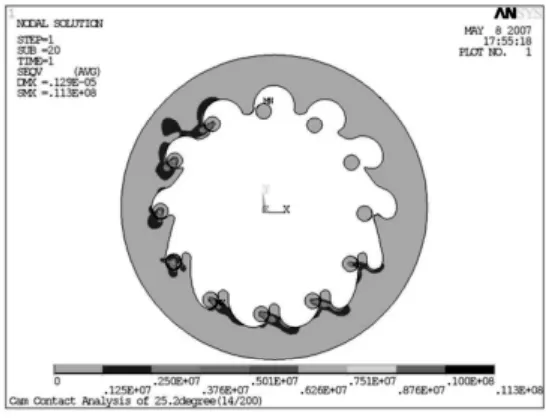
图11 外载荷最大时的应力云图

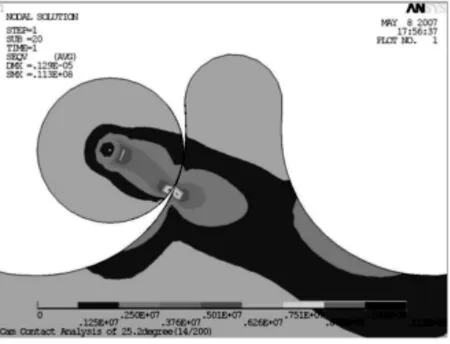
图12 实际的最大应力位置

图12 为θH=25.2°时凸轮与4 号针齿接触的应力云图，其中第1 号针齿位于坐标轴X 正向上，各针齿的序号以顺时针方向依次排列。由图可知，凸轮——针轮啮合副的最大接触应力并未发生在凸轮和针轮接触点处，而是靠近凸轮廓线的齿根部位。究其原因，若其连接部分是直角时，最大弯曲应力应发生在拐角处，而实际上，凸轮的齿根部位是圆滑过渡的，从而使得最大应力点向上发生偏移。说明该类机构中凸轮齿的弯曲应力高于其接触应力。

通过上述有限元法的分析结果可以提取每个离散位置处凸轮和针齿啮合时的最大应力值。为便于比较，将上述结果绘制成表格，如表3 所示。

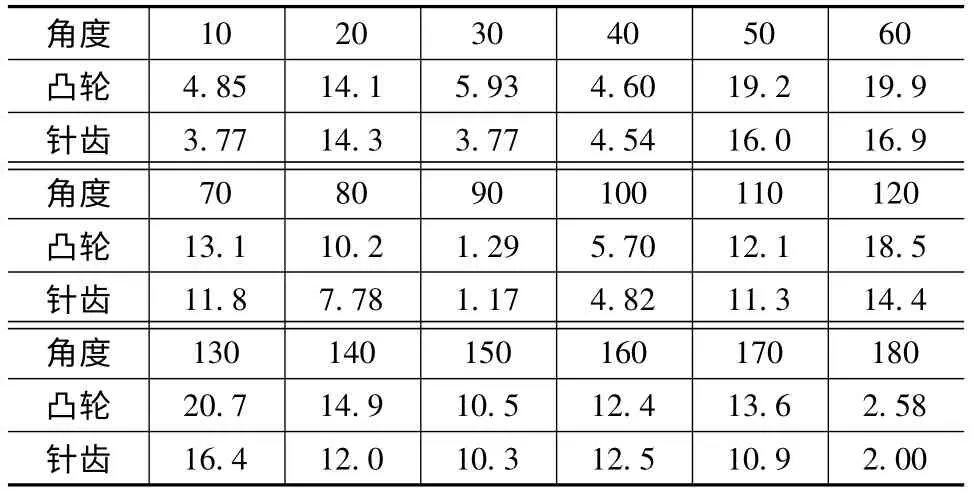
表3 凸轮和针齿在不同位置的最大应力(单位:MPa)

由表3 可以看出，在机构一个运动周期内，凸轮的最大应力发生在θH=130°时，其值为20.7MPa;针齿的最大应力发生在θH=60°，其值为16.9Mpa。二者的最大应力皆不发生在外载荷最大的时候(θH=25.2°或θH=158.4°，Tmax=145Nm)。究其原因，是由于在外载荷最大位置处，机构中参与啮合的凸轮——针齿副啮合对数较多，使得单对啮合副上的载荷降低。

2.3 有限元法与理论计算结果的对照

无论是理论分析方法［7］，还是有限元法，都可以得到每个针齿在机构运转一周内所受到的啮合力大小。为便于比较，将两种方法的结果分别绘制成曲线图，如图13 所示(篇幅所限，紧列出部分针齿的啮合力和总啮合力)。图中，右侧为有限元方法得到的啮合力，左侧图为理论分析方法得到的啮合力。第1 号针齿位于坐标轴X 正向上，各针齿的序号以顺时针方向依次排列。

图13 两种方法啮合力图的对比

图13 中横坐标是机构运转一周的无因次时间，纵坐标是啮合力。从左右两组图的对比可以看出，由两种模型求解出的应力曲线的变化趋势基本相同，曲线的峰值和谷值的个数及对应的位置基本相同，其数值的大小也非常接近，只是前者的应力值要略高于后者的应力值。总体而言，两种方法的结果比较吻合的。

但需要说明的是，本文采用的有限元法具有一些理论计算无法替代的优点:

(1)有限元模型中考虑了机构中各个弹性环节的变形，更贴近实际的工作状况，因而能更为准确地揭示机构的真实受力状况。而理论模型中，凸轮——针轮的啮合被近似为点接触，其啮合刚度低于实际值，因而使得所求出的接触应力高于由有限元方法求出的应力值。

(2)有限元方法能够揭示出机构中应力/应变的分布规律，能更全面地反映机构的受力状况，能准确计算出最大接触应力及其发生的部位，从而为结构设计和改进提供了可靠的力学依据。

3 结论

环板式行星分度凸轮机构通过SolidWorks2010中Motion 分析进行了动力学计算，又采用ANSYS 进行强度分析，得到如下结论:

(1)环板是环板式行星分度凸轮机构的主要设计零件，阔线设计符合预计的运动规律。最大应力发生在凸轮廓线靠近齿根的部位，而非凸轮和针齿的接触点，说明该类机构中凸轮齿的弯曲应力高于其接触应力，因此在设计该类机构时，应对凸轮齿的强度加以一定的考虑。

(2)针齿上安装轴承时，轴承的强度要进行充分考虑。

(3)有限元方法比理论分析方法的优点突出，能够模拟实际的工作状况，更为准确地揭示机构的真实受力状况，为结构设计和改进提供了可靠的力学依据。

［1］张策，杨玉虎，叶青，等. 平面行星分度凸轮机构［J］. 机械科学与技术，1996，15(6):871－873.

［2］Figliolini G.，Rea P.，Angeles J. The pure-rolling cam-equivalent of the Geneva mechanism ［J］，Mechanism and Machine Theory，2006，41:1320－1335.

［3］Wang H.，Zhang C.，Lin Z.Q.，et al. Meshing analysis of the planetary indexing cam mechanisms ［J］，ASME J.Mech. Des.，2005，127:340－346.

［4］王皓，张策，杨玉虎. 行星分度凸轮机构凸轮廓线的设计［J］. 机械工程学报，2003，39(3):13－16.

［5］张策，刘明涛，杨玉虎. 新型行星分度凸轮廓线设计及仿真［J］. 天津大学学报，2006，39:100－103.

［6］陈新动，张策，刘明涛，等. 双环式行星分度凸轮机构的平衡分析和样机实验研究［J］. 机械科学与技术，2006，25:142－145.

［7］刘明涛. 行星分度凸轮机构的创新设计与研究［D］. 天津:天津大学，2005.

［8］田广才. 环板式行星分度凸轮机构的强度与模态分析［D］. 天津:天津大学，2007.

［9］冯晓梅，孙开元，张大卫. 基于ANSYS 的高速精密定位平台有限元分析［J］. 组合机床与自动化加工技术，2009(9):76－80.

［10］赵志彬，贺尔铭，何秋荣，等. 基于ANSYS 的飞机炮舱段结构模态分析与结构优化［J］. 机械科学与技术，2008，27(3):297－300.