双圆弧齿轮传动多目标优化设计

郭 波，邹丽梅

(武夷学院 电子工程系，福建 武夷山 354300)

0 引言

双圆弧齿轮传动是近几十年发展起来的一种新型齿轮传动。它具有承载能力高、使用寿命长以及能在高速和重载条件下工作的特点。目前国内外针对双圆弧齿轮传动系统的研究尚处于初级阶段。从它的基础理论、设计方法到实际应用，还有许多问题有待解决。

双圆弧齿轮的齿形参数直接影响着双圆弧齿轮的承载能力和传动性能，而齿轮参数的优化设计还是目前研究中的薄弱环节。本文根据齿轮啮合原理、双圆弧齿轮的设计方法和规范，摈弃传统的多目标优化设计方法，对现有的用于两目标优化设计的粒子群优化设计技术加以改进，给出约束3 目标现代优化设计方法，在追求综合性能最优的前题下对双圆弧齿轮的齿形参数进行优化，以充分发挥双圆弧齿轮传动系统的潜能，达到最佳的技术经济指标。

1 纵向重合度

纵向重合度εβ对双圆弧齿轮的承载能力、振动和噪声有重大的影响。合理选用重合度，可以提高齿轮传动的承载能力，减轻振动和噪声。

重合度由整数部分με和尾数部分Δε 组成:

选取较大的重合度，可以提高传动平稳性和承载能力。但是采用大重合度时，传动系统对齿距误差、齿向误差、轴线平行度误差和轴系变形量会特别敏感。因此采用大重合度时，必须严格限制齿距误差、齿向误差、轴线平行度误差和轴系变形量。否则不能保证几个接触迹均匀地承担载荷，不能达到传动平稳和应有的承载能力。

尾数Δε 取得太小时，则当接触迹进入或脱开齿面时，端部齿根弯曲应力过大，容易引起齿端崩角。随着尾数的增大，端部应力将有所减小。但Δε 增大到0.4 以上之后，应力减小缓慢。Δε 取得太大时，增加了齿宽而不能使每一瞬间都增加接触迹数目［1］。

整数部分με的常用范围为1 ～6，尾数部分Δε的常用范围为0.2 ～0.4。

综上所述，为选取适宜的纵向重合度，本文改变传统的设计方法中将重合度作为约束条件的做法，而将重合度作为一个追求的目标函数。

2 齿面相对主曲率

圆弧齿轮的啮合齿面是一对共轭齿面。一对共轭齿面的曲率情况用相对主曲率来表征。

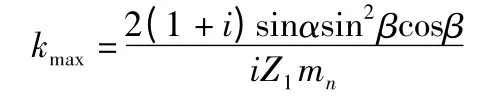
式中:kmax—齿面相对主曲率，mm－1;

i—传动比;

α—压力角，(°);

β—螺旋角，(°);

Z1—小齿轮齿数;

mn—模数，mm。

根据Hertz 弹性接触理论，齿面相对主曲率越小(即相对曲率半径越大)，齿面接触应力越小，接触强度越高;根据弹性流体动力润滑理论［2］，齿间最小油膜厚度越大，抗胶合能力越强。因此，以追求齿面相对主曲率最小作为第二个目标函数。

3 双圆弧齿轮传动约束多目标粒子群优化设计

为使双圆弧齿轮传动获取最佳的技术经济效果，本文以纵向重合度在一定条件下最大、齿面相对主曲率最小及齿轮传动总体积最小为同时追求的三个目标函数，这是一个3 目标优化问题。3 个目标没有公度性，且相互关联、相互制约、相互冲突，不宜用传统的多目标优化方法进行处理。这是因为传统的多目标优化方法是将3 个子目标通过权重的设置聚合成一个带正数的单个目标函数进行优化，系数由决策者决定，或者由优化方法自适应调整。传统方法在处理这类问题时至少存在着如下两个缺陷:首先，3 个目标函数没有相同的物理含义，量纲不一致，没有可比性，将3 个目标函数转化为一个单目标函数缺乏科学性;其次，通过权重的设置将多目标问题转化为单目标问题，带有较浓重的主观色彩，难以反映客观真貌。权重的设置要求设计者有长期的研究经验和厚重的领域知识，稍有偏差就会大大影响多目标最优解的产生，因此合适地选取权重并非易事。

粒子群优化算法(particle swarm optimization，PSO)［3-4］在解决约束多目标优化问题中得到有效应用。在文献［5-6］中提出的寻优原则和搜索方法基础上，给出本文范例约束3 目标粒子群优化算法。算法并非将3 个子目标函数通过权重的设置聚合成为一个单目标进行优化，而是首先在可行域内初始化一个粒子群体，然后通过各个子目标函数共同指导每个粒子在可行域中向3 个目标函数不同时增大的方向一步步搜寻，最终使粒子落入非劣最优目标函数空间。

具体实现要点如下:①以纵向重合度的倒数f1(X)、齿面相对主曲率f2(X)及双圆弧齿轮传动总体积f3(X)中的每个目标函数，找到粒子群体中相对应的全局极值G［j］(其中j =1，2，3 是目标函数的个数)和每个粒子的个体极值P［i，j］(其中i =1，2，…，N是粒子群体中的粒子个数)。②在更新每个粒子的速度(相当于有向步长)时，用各个G［j］的均值g 作为全局极值。③每个粒子的个体极值P［i，j］是通过判断矢量P［i，j］相对于矢量G［j］的离散程度来决定，是取P［i，j］的均值，还是在P［i，j］中随机选取。

算法流程如下，①给定算例粒子群规模N，在可行域内随机产生各粒子的位置Xi和速度Vi(i=1，2，…，N)。②用目标函数f1(X)、f2(X)和f3(X)分别计算每个粒子的适应度值。③在f1(X)、f2(X)和f3(X)下分别对每个粒子求得个体极值。④对f1(X)、f2(X)和f3(X)分别求三个全局极值。⑤计算三个全局矢量的均值g 和每两个全局矢量之间的距离d。⑥计算每个粒子个体极值之间的距离dP［i］。⑦对每个粒子计算更新速度Vi和位置Xi时所用的个体极值Pi，如果dP［i］＜d，则在每个粒子对于f1(X)的个体极值P［1，i］、对于f2(X)的个体极值P［2，i］和对于f3(X)的个体极值P［3，i］之间随机选取一个个体极值作为Pi;否则，取P［1，i］、P［2，i］和P［3，i］的平均值作为Pi。⑧用⑤、⑦所得的g 和Pi按下式更新每个粒子速度Vi(表征搜索方向和步长)和位置Xi:

式中，ω 为惯性因子，c1和c2是学习因子，rand()和Rand()是介于(0，1)之间的随机数。更新后检验每个新粒子是否在可行域内，若不在可行域内，则重更新，直到在可行域内为止。⑨设置循环迭代次数。若达到该次数，结束;否则回②。

4 优化范例

4.1 算例描述

功率P=9000kW，转速n1=6054r/min，n2=1485r/min，每天24 小时连续运行，持久寿命设计。大小齿轮材料均选用42CrMo，单级人字齿轮结构，齿形为GB/T12759-1991 标准双圆弧齿廓，齿轮精度不低于6 级(GB/T15753-1995)。

4.2 选取5 个设计变量

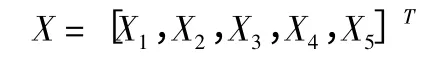
式中:X1—小齿轮齿数;X2—法向模数;

X3—齿宽系数;X4—螺旋角;

X5—齿端修薄长度。

4.3 建立目标函数

(1)将纵向重合度

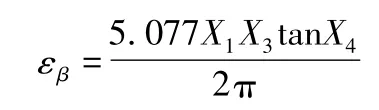
(2)将齿面相对主?曲率

最小作为第二个追求的目标;

(3)将齿轮传动总体积

最小作为第三个追求的目标;

4.4 确定约束条件

依据文献［7］和工程经验确定齿面接触疲劳强度约束条件、齿根弯曲疲劳强度约束条件、齿宽系数约束条件、齿端修薄长度约束条件及限定设计变量的上下界。

4.5 优化计算

用MATLAB 进行程序设计计算，循环300 次，结果得到60 组可行解及相应的目标函数值，非劣最优目标域如图1 所示。

图1 非劣最优目标域

决策者可根据自己的偏好选择其中的一组解作为最终方案。例如，选择综合性能都较佳的第22 组解作为最终方案:

式中:φα—齿宽系数;

δ—齿端修薄长度;

其它符号意义同前。

5 结论

(1)本文给出了3 目标粒子群优化方法，并对范例成功地进行了优化，优化设计出的双圆弧齿轮传动即具有较高的接触强度、抗胶合能力、较好的平稳性及啮合特性，又具有较低的产品成本。能够充分地发挥摆针传动系统的潜质，比传统的多目标优化设计方法及通过每一单目标进行优化的现代方法具有明显的科学合理性。

(2)由于其它齿轮的设计计算与双圆弧齿轮传动有相似的原理，可以将本文的优化方法拓展到其它齿轮传动中。该方法对于其他相类似的复杂机械传动系统的约束多目标优化研究也具有一定的适用价值。

［1］陈谌闻. 圆弧齿圆柱齿轮传动［M］. 北京:高等教育出版社，1995.

［2］温诗铸，黄平. 摩擦学原理［M］. 北京:清华大学出版社，2002.

［3］Kennedy J，Eberhart R. Particle swarm optimization［C］//IEEE International Conference on Neural Networks:Perth，Australia Piscataway NJ:IEEE Service Center，1995:1942－1948.

［4］Eberhart R，Kennedy J. A new optimizer using particle swarm theory［C］//Roc. Sixth International Symposium on Micro Machine and Human Science:Nagoya，Japan Piscataway，NJ:IEEE Service Center，1995:39－43.

［5］张敏. 约束优化和多目标优化的进化算法研究［D］. 合肥:中国科学技术大学，2008.

［6］张利彪，周春光，马铭，等. 基于粒子群算法求解多目标优化问题［J］. 计算机研究与发展，2004，41(7):1287－1290.

［7］齿轮手册编委会. 齿轮手册［M］. 北京:机械工业出版社，2005.