弧形齿万向轴外齿的包络法加工计算*
孙兴伟,葛 干,王 可
(沈阳工业大学 机械工程学院,沈阳 110870)
0 引言
当前螺杆钻具万向轴的种类,主要为球笼式和花瓣式:对于球笼式万向轴,以钢球传递扭矩和速度,传动平稳、容易润滑、导向灵敏,但加工难度高。由于钢球工作接触面积小,因此传递扭矩小,接触面容易产生疲劳,使用寿命短[1]。花瓣式万向轴,加工方便、传动扭矩大、转角大,但传动不平稳、加工精度低、机械效率低、磨损厉害,故使用寿命较短[2]。
弧形齿万向轴作为一种新型的螺杆钻具万向轴,不仅很好地克服了以往万向轴所存在的传动不平稳、磨损厉害、加工精度低、机械效率低等缺点,具有结构简单、润滑良好、大摆角、大扭矩、使用寿命长等优点[3]。
对于弧形齿万向轴的外齿加工,考虑到盘形铣加工的经济性,高效性,表面加工质量好等优点,但对其采用平面包络计算方法计算刀具轨迹时,存在着加工维度低、盘形铣刀在齿根处与已加工表面产生干涉现象的问题,从而导致加工工艺失败。为了增加加工维度,避免干涉,本文采用空间包络计算方法,计算加工弧形齿万向轴外齿齿面的刀具运动轨迹。
1 刀具和工件模型的建立
要进行外齿齿面的包络分析,首先必须建立其刀具、工件的几何数学模型。
1.1 坐标系以及坐标转换
S(o,x,y,z)坐标系,为与外齿固连的工件坐标系,如图1 所示:z 轴与万向轴的轴线重合。S1=(O1,x1,y1,z1)坐标系,为与刀触点(即刀具铣削面与加工面实际接触的点)固连的动坐标系,如图2 所示:原点o1在S(o,x,y,z)坐标系的坐标为(x0,y0,z0);y1轴与y 轴夹角α 为外齿绕z 的转角;z1轴与z轴夹角θ 为刀具旋转角。S'(O,X,Y,Z)坐标系,为与机床固连的机床坐标系,如图3 所示:原点O 与原点o 重合;X 轴与x 轴夹角α 为绕Z 轴的转角;Z 轴与z 轴平行;S″(O1,X1,Y1,Z1)坐标系,为与刀具固连的刀具坐标系,如图4 所示:X1轴与x1轴平行;Y1轴与y1轴平行;Z1轴与z1轴平行。
1.2 坐标系转换关系
S1坐标系转换到S 坐标系转换关系为:

图1 S 坐标系

图2 S1 坐标系

图3 S'坐标系

图4 S″坐标系

S 坐标系转换到S'坐标系转换关系为:
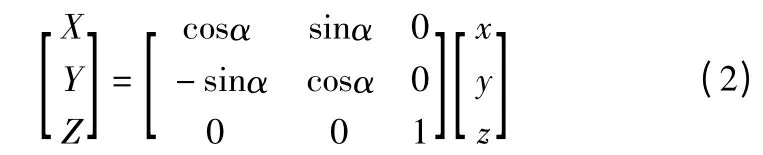
式中:θ— 刀具旋转角;α—工件旋转角度;
(x0,y0,z0)—S 坐标系下刀触点坐标。
1.3 刀具模型
包络法加工外齿,通常采用盘形铣刀,铣削面为由圆环面过渡的双锥曲面。在包络加工时,回转锥面起到切削金属的作用,工件已加工表面则是由刀尖圆弧部分回转形成的圆弧面包络成型。因此,可以将刀具简化成圆环面模型,如图4 所示。铣削面上刀触点(铣削点)的运动轨迹组成了铣削轨迹束。
1.4 工件模型
外齿齿面为椭球面[4],为了简化问题,我们只以齿1 为研究对象,其他齿面迎刃而解。S 坐标系下的齿面方程为:

式中:R—基圆半径;a—椭球短轴;b—椭球长轴。
2 刀位点方程的建立
在S 坐标系下,刀触点运动轨迹所在铣削平面∑1的平面(平面y1o1z1),与椭球齿面∑2所交的空间曲线即为齿面上与刀触点运动轨迹相切的空间曲线Γ,如图5 所示。因此,通过空间曲线Γ 的切向量,可以计算出刀触点运动轨迹的圆心。由于该圆心又与刀位点(图5 中M1点)运动轨迹的圆心同位于盘形铣刀的轴线上,且两轨迹所在平面平行,进而可以推算出刀位点坐标。
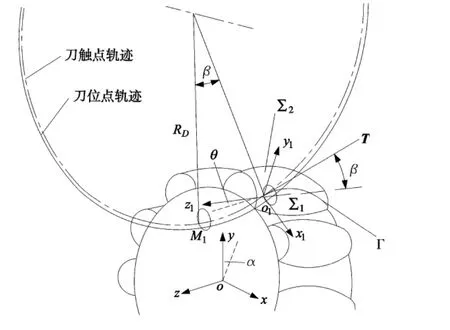
图5 刀具与工件空间位置关系
为了简化计算,我们在刀触点建立动坐标系S1=(01,x1,y1,z1),坐标原点o1与刀触点重合。首先在该坐标系下,求刀位点的坐标,然后通过坐标转换,求其在S(o,x,y,z)坐标系下的坐标,最后,再通过坐标转换到机床坐标系下。
2.1 铣削角的计算
求取在S1=(01,x1,y1,z1)坐标下的刀位点坐标之前,首先必须先求出铣削角β,它是刀位点运动轨迹半径计算的关键。所谓的铣削角β,就是在铣削平面∑1内,曲线Γ 在刀触点的切向量与z1轴的夹角。
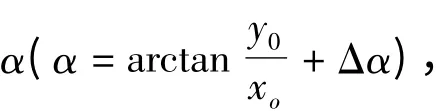
刀具切削平面Σ1在S1坐标系下的法向量为:

根据式(1)可转换到S 坐标系下得:

设点M(x,y,z)为平面Σ1任意一点,由于M0(x0,y0,z0)在平面Σ1上一点,则向量M0M必与平面Σ1的法向量n 垂直,即它们的向量积为零:

则刀具切削平面Σ1的方程为:
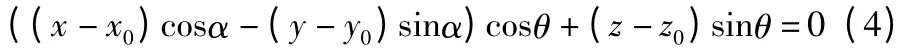
联立(3)、(4),可得空间曲线Γ 的方程为:

(5)其参数方程形式为:

根据雅克比(Jacobi)公式[6]可得:

其中:
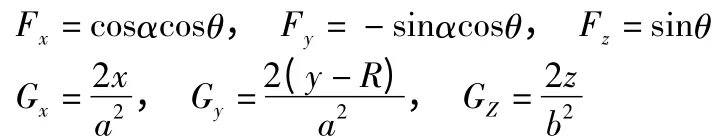
化简得:
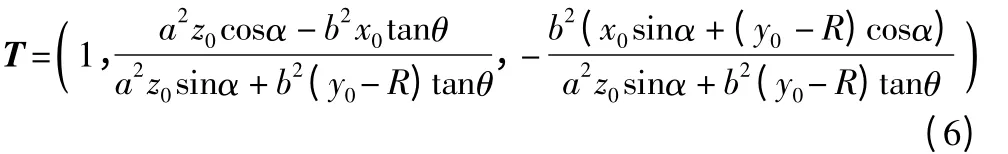
z1轴在S1坐标系下为:z1=(0,0,1)
根据式(1)可转换到S 坐标系下得:

2.2 刀位点坐标计算
在S1坐标系内,刀触点M 与刀位点M1存在偏置,其偏置量计算如下:
x1方向的偏置:

y1方向的偏置(参看图5):

S1坐标系内,刀位点坐标为:

式中:RD—刀触点运动轨迹的半径;
r—刀尖半径;R刀—盘刀半径。
经过坐标变换即可求得刀位点的坐标。
3 数学模型的求解
加工椭球面需要五个伺服变量,其中三个直线坐标和两个旋转坐标。(x,y,z)为直线坐标,盘形铣刀旋转角θ 以及工件旋转角α 为旋转坐标。为增强系统的稳定性,降低加工维数,在铣削椭球面某一截面时,使z 坐标为定值。建立盘形铣刀旋转角度θ 与刀位点z 坐标建立一一对应关系。
设在加工M0(x0,y0,z0)时,刀位点z 方向坐标为c。根据式(1)可得方程:

将整理后的刀位点的坐标代入式(9)并整理可得:

为了求解未知量θ,我们令w=tanθ,定义函数f(w):
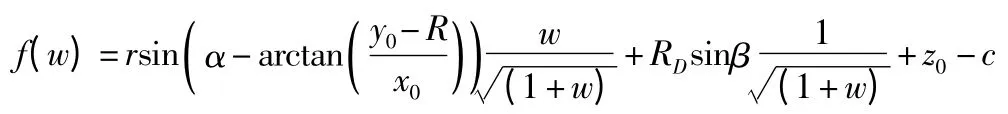
这里转化成关于变量w 的函数,考虑到这里直接求方程的解析解存在着困难,可以借助搜索法进行迭代,求解方程的近似解。
搜索法步骤如下:
步骤1:选定初始点w0和步长h、计算精度ε,置k=0;
步骤2:比较函数值的大小。若f(wk)≤ε,转步骤4,若f(wk)>ε,转步骤3;
步骤3:寻找下一点。令wk+1=wk+(k +1)h 计算f(wk+1),若f(wk+1)≤ε,wk=wk+1,转步骤4;若f(w0)>ε,令k=k+1;转回步骤3;
步骤4:x=wk。
按上述方法,求解出w,进而求解出θ,至此,(x,y,z,α,θ)五个变量都已经确定,那么机床的运动轨迹也就确定。
4 应用实例
现在以螺杆钻具172 型号用弧形齿万向轴为例,计算其包络法加工坐标。其尺寸参数为:齿数8个,a=b=11,c=25,R=39.5,r=1.2,R刀=145。
由于数据点过多,现任取其中的z0=8 截面的廓形数据,如表1 所示,代入式(8)、式(10)得到的刀位点M1的坐标,见表2。利用UG 三维软件进行仿真的结果如图6 所示。

表1 廓形数据点表

(续表)

表2 对应刀位点
取z0=8 处的截面仿真廓形数据与理论廓形数据进行对比,其径向误差为:
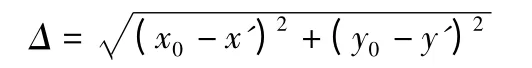
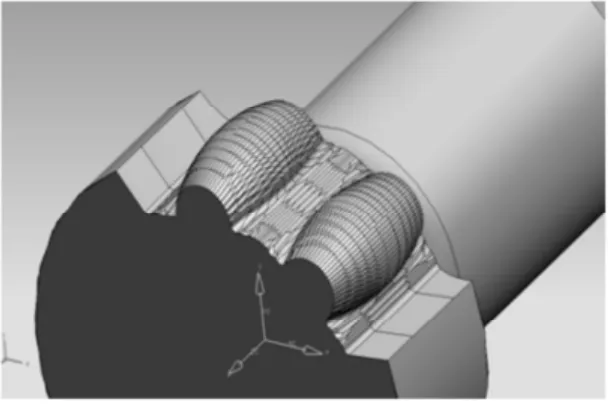
图6 仿真效果图
表3 为其径向误差Δ 在各点处误差值,其分布如图7 所示。

表3 仿真廓形点以及径向误差
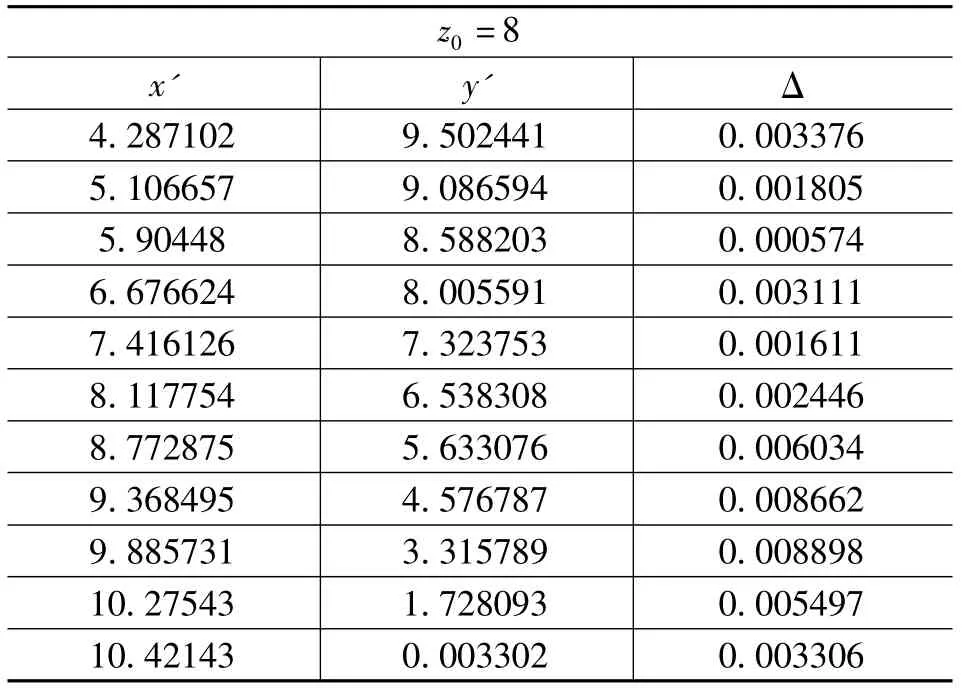
(续表)
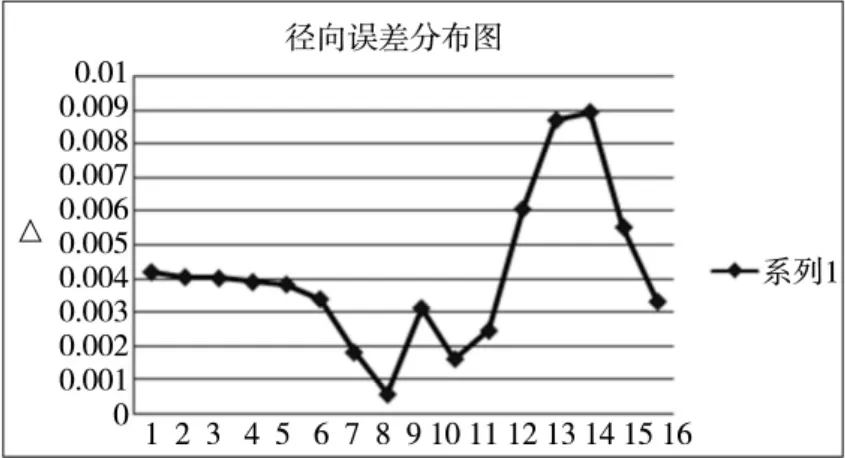
图7 径向误差Δ 分布图
通过表3、图7 可见,仿真出来的齿面廓形与理论廓形之间的最大径向误差不超过0.009mm,满足加工工艺精度要求。但在点7-15 出现误差变化大的原因,是主要由于加工这些点时盘形铣刀摆角角度变化大以及廓形计算时小数省略的原因造成。
5 结论
本文提出的基于空间包络法加工万向轴外齿面的刀位点的计算方法,虽借鉴于螺杆成型方法,但又有自己的特点:①加工时,盘刀中心、刀位点、工件中心不在一条直线上,避免刀具与已加工齿面产生径向干涉;②B 伺服轴,旋转角度不断变化,以适应空间包络要求,避免产生轴向干涉。③通过UG 三维软件进行仿真可以发现,该刀具轨迹计算方法具有计算精度高,加工表面质量好,刀具过程干涉小等优点。
[1]刘凤波,辛明金,崔雯辉. 轻型汽车球笼式万向节设计[J]. 辽宁省交通高等专科学校学报,2010,12(1):14-18.
[2]董卫国. 花瓣式万向节的使用现状及改进[J]. 中国科技信息,2008(19):115-117.
[3]于风春. 弧形齿万向联接轴附加弯矩计算技术的开发[J]. 冶金设备,2010,6(3):49-51.
[4]张延. 基于FANUC 宏程序的三轴不相等半凸型椭球面加工[J]. 制造业信息化,2009,7(3):352-355.
[5]同济大学应用数学系. 高等数学(下册)第五版[M]. 北京:高等教育出版社,2006.
[6]石鸿雁,苏晓鹏. 优化方法(第一版)[M]. 大连:大连理大学出版社,2009.
[7]王金铭,刘艳秋,陈欣. 数值分析[M]. 大连:大连理工大学出版社,2007.

