基于ANSYS 分析的螺栓组拧紧工艺研究*

马 跃，王 崴，徐 浩，徐晓东，刘晓卫

(空军工程大学 防空反导学院，西安 710051)

0 引言

螺栓组连接结构广泛存在于机械行业的各个领域。据统计，航空发动机上40% ～50%的零件为螺钉，波音747 上的螺栓数高达250 万个。螺栓组拧紧过程中，由于螺栓间相互弹性作用，后拧紧的螺栓对先拧紧的螺栓会造成干扰，导致螺栓组各螺栓之间残余预紧力不等，结合面面压分布不均，严重影响螺栓组的连接性能。尤其是对具有密封要求和精密装配的螺栓组连接结构。因此，研究合适的螺栓组拧紧工艺，对整个机械行业十分重要。

在螺栓组拧紧工艺研究方面，国内外学者做了大量研究工作:在国外，Bibel 等［1］通过试验研究了螺栓的弹性相互作用，发现法兰垫片螺栓连接中，由于弹性相互作用预紧力会不同程度的丢失，并通过构建基于应力的弹性相互作用矩阵，来调节达到要求的夹紧力所需的初始预紧力;Fukuoka 等［2-3］采用仿真分析结合试验研究了不同拧紧顺序对弹性相互作用的影响，通过一定的拧紧顺序改善了夹紧力分布的均匀性;Nassar 等［4-5］研究了拧紧速度对载荷传递的影响，得出力的施加速度与结合面面压间的关系。在国内，西安交通大学杨国庆等［7］运用ANSYS 和弹性相互作用理论，构建了初始预紧力和结合面面压分布的关联模型，进而运用该模型求解满足某汽车发动机密封性能要求所需的初始预紧力;西安交通大学陈成军等［8］运用有限元模拟螺栓组拧紧过程，构建螺栓组连接弹性相互作用模型，为螺栓组装配连接工艺设计和性能预测提供了参考;朱正德［9］等通过对拧紧后设备能力的验证，阐述扭矩拧紧控制的实质，提出改善螺栓连接质量的工艺途径。

对于螺栓组拧紧工艺的研究，学者们对螺栓的拧紧顺序和拧紧速度研究较多，而对分步拧紧对螺栓组拧紧效果的研究较少。本文以某型发动机盘式连接螺栓组为研究对象，运用大型有限元仿真软件ANSYS，研究分步加载对螺栓组连接性能的影响规律，并据此对原有工艺进行优化，指导装配工艺设计。

1 螺栓组连接有限元模型的建立

1.1 发动机盘式连接螺栓组几何模型

发动机盘式连接螺栓组由24 个螺栓连接，结构过于复杂(如图1)，不利于在ANSYS 中计算分析。因此，本文在不影响所研究的结构特点的前提下对其进行了简化，由24 个螺栓精简为6 个螺栓，不考虑螺栓螺纹结构，用圆柱体等效。上、下盘外径50mm，内径30mm，盘厚均为5mm，螺栓孔直径为8mm，结构如图2 所示。

图1 发动机盘式连接

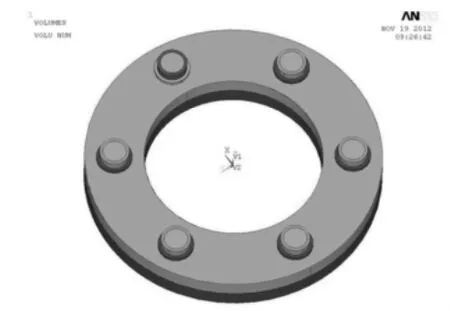
图2 盘式连接螺栓组几何

1.2 发动机盘式连接螺栓组的有限元模型

在ANSYS 中建立好盘式连接螺栓组几何模型后，定义各部件材料属性，如表1 所示。

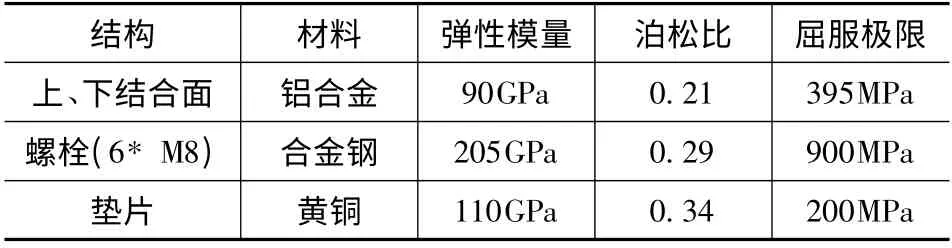
表1 模型各部分材料属性

除垫片采用SOLID186 单元划分网格外，其余均用六面体单元划分网格。选用TARGE170 面-面接触单元定义螺栓和上、下板间接触，选用CONTA174 面-面接触单元定义上、下板与垫片接触。选用PRETS179单元模拟螺栓的预紧和卸载，结构如图3 所示。螺栓连接几何模型的建立，材料属性的定义，面-面接触单元的选取，迭代运算的设置等全部运用ANSYS 自带的APDL 语言进行编写，其有限元模型如图4 所示。

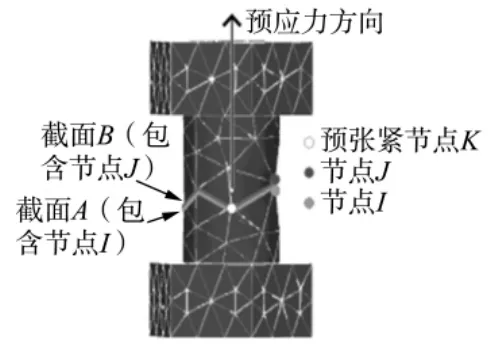
图3 PRETS179 单元

图4 盘式螺栓组有限元模型

2 螺栓组分步拧紧有限元分析

2.1 螺栓组拧紧方式

螺栓组拧紧的先后顺序和力的加载速度均会对连接性能造成影响。由文献［2］可知，呈环形分布螺栓组按对角顺序拧紧时，螺栓间的弹性相互作用最弱，残余预紧力和面压分布最均匀，拧紧效果最好，因此，本文采用的螺栓拧紧顺序为对角拧紧，如图5所示。鉴于拧紧速度对连接性能也会产生影响［4］，本文每个分步载荷加载时，均采用在10S 内匀速加载至分步目标载荷的方法。

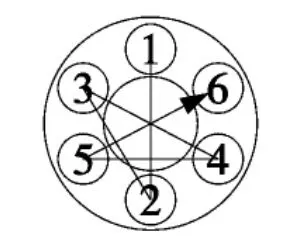
图5 螺栓组对角拧紧顺序

2.2 分步加载分析

编写APDL 程序时，运用SLOAD 命令设置螺栓组的分步加载。设螺栓拧紧初始预紧力F 为15KN，分i 步加载，每步加载较上一步递增15/iKN 的预紧力，共有2i 个载荷步，在第2i－1 步施加载荷，在第2i 步锁紧载荷。i 分别取1、2、3、4、5、10、15，选择垫片显示应力分布云图如6 至图11 所示。

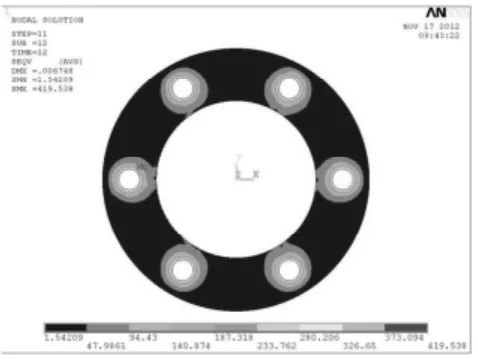
图6 1 次分步加载

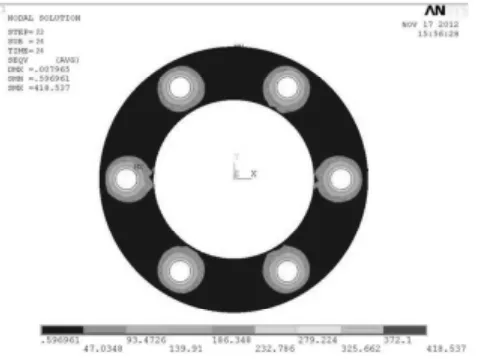
图7 2 次分步加载

图8 3 次分步加载

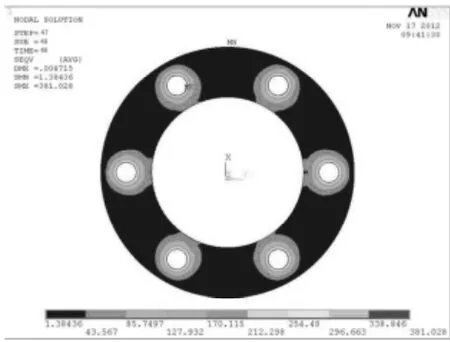
图9 4 次分步加载

图10 5 次分步加载

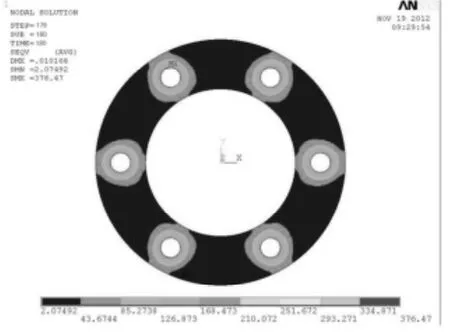
图11 13 次分步加载

运用PRNLD 命令提取各个螺栓残余预紧力，如表2 所示。

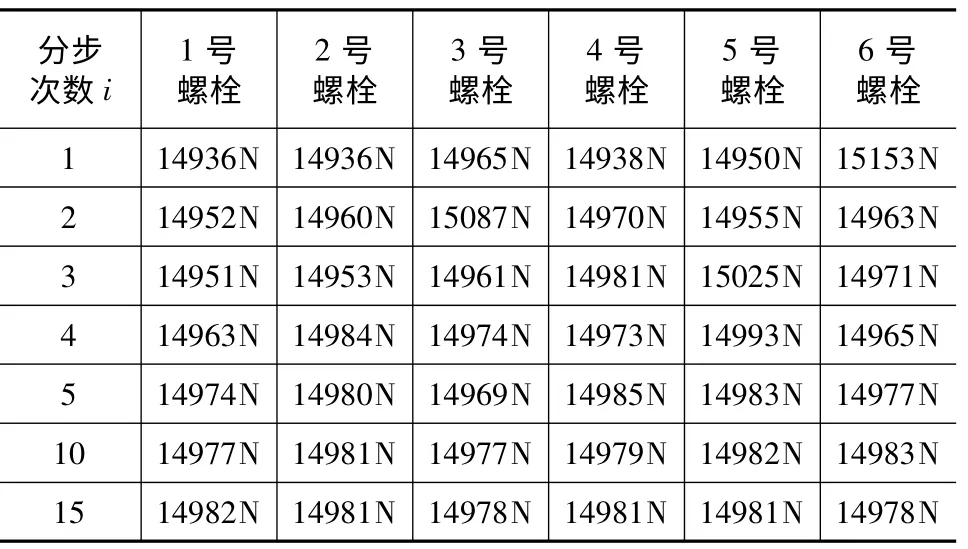
表2 不同分步螺栓残余预紧力提取值

由标准差计算公式:

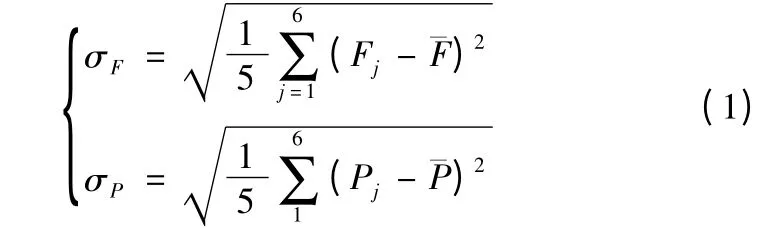
可知:当i 分别取1，2，3，4，5，10，15 时，各螺栓残余预紧力标准差分别为87.58，55.33，27.53，10.47，5.93，1.74，1.72。同理，提取并计算各螺栓半径8mm内平均应力标准差为:3.2421，2.7103，2.2637，1.9986，1.8362，1.5943，1.5388。本文还分析了顺序拧紧残余预紧力和接触应力标准差随分步次数的变化规律，通过对比进一步揭示分步加载对螺栓残余预紧力和结合面面压的影响规律，如图12，13 所示。

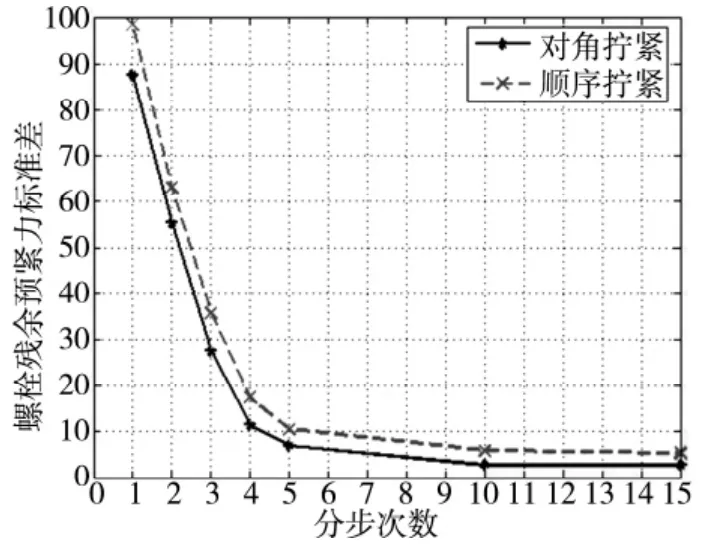
图12 残余预紧力标准差变化图

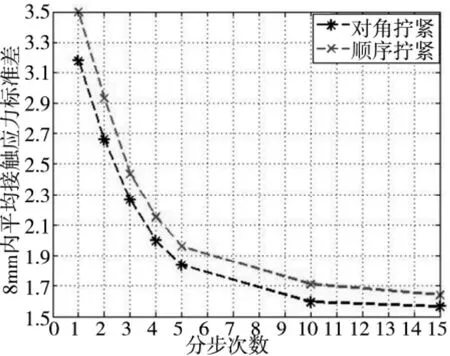
图13 8mm 内平均接触应力标准差变化图

由上图可知，对角拧紧和顺序拧紧均遵循如下规律:

(1)随着载荷加载分步步数的增加，螺栓间残余预紧力和结合面接触应力标准差降低。

(2)螺栓残余预紧力和结合面接触应力标准差在5 次分步加载以前减小趋势较大，5 次分步以后几乎不再变化，趋于平稳。

3 某型发动机盘式螺栓组拧紧工艺优化

3.1 螺栓组拧紧优化工艺的提出

根据某型发动机盘式螺栓组现有装配要求，满足其正常使用功能须在每个螺栓上加载28N·m 的力矩。传统拧紧工艺为:按照图5 所示对角拧紧顺序，先加载32N·m 的力矩，保持45 分钟，完全卸载，再用28N·m 的力矩一次拧紧，流程如图14a 所示。在拧紧螺母时，将双头螺栓顶端固定在保持器上以免发生转动。先加载至32N·m 是为了使螺栓充分拉伸，防止螺纹牙错齿、滑丝，同时加工硬化增加其连接强度。

由前文研究可知，分步拧紧可以降低结合面应力分布标准差。为了改善螺栓组连接性能，使结合面应力分布更加均匀，本文对传统拧紧方式提出一种改进的拧紧工艺，即对两次加载均采用二次分步加载，具体方案如图14b 所示。并以仿真计算得到的各螺栓周围8mm 范围内的平均接触应力标准差作为衡量指标，评判对原有工艺的优化效果。

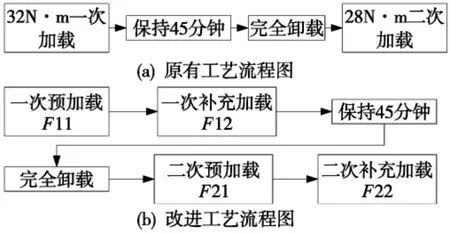
图14 改进前后工艺流程图

3.2 优化工艺与原工艺分析比较

由于在ANSYS 中施加的是螺栓预紧力，所以须将施加力矩转换为预紧力，由公式:

式中:T—扭矩;

K—扭矩系数，本文取0.2331［10］;

D—为螺栓直径，本文取8mm;

计算得28N·m 的力矩约为15000N，32N·m 的力矩约为17500N。

对原有工艺，编写APDL 程序，用TIME 命令设置保持时间，RESTART 表示卸载，输入ANSYS 中进行运算分析。

在改进工艺中，为了得到最优的一次预加载荷F11，一次预加载荷分别取一组数据，补充载荷取定值17500N，在ANSYS 编写程序仿真，提取并计算第一次初始预紧力对接触应力标准差的影响，如图15a 所示。

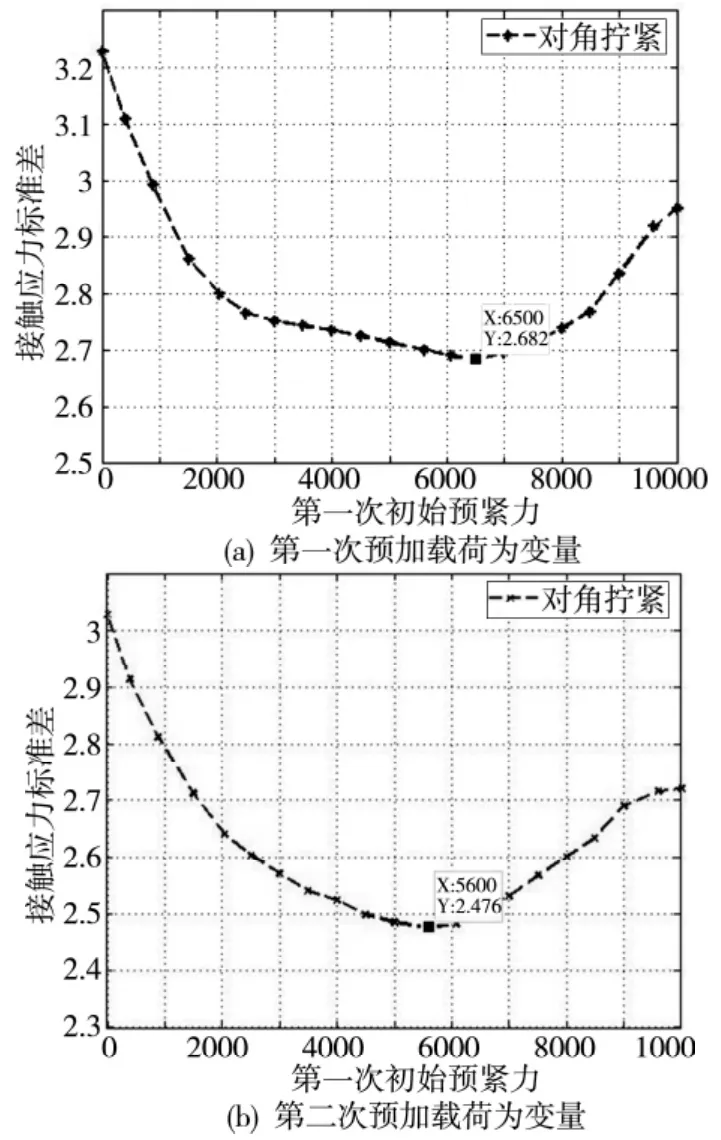
图15 初始预紧力和接触应力标准差关系图

由拟合曲线可知，当第一次初始预紧力取值6500N 时，接触应力标准差最小。设定保持时间然后卸载。在ANSYS 中进行第二次分步加载，运用相同方法，得到当第二次初始预紧力F21 为5600N 时，接触压力标准差最小，如图15b 所示。

由此可以得到，改进后拧紧工艺为:一次预加载6500N→一次补充加载17500N→保持45 分钟→卸载→5600N 二次预加载→15000N 二次补充加载。

提取并计算改进前后螺栓8mm 内平均应力值如表3 所示。

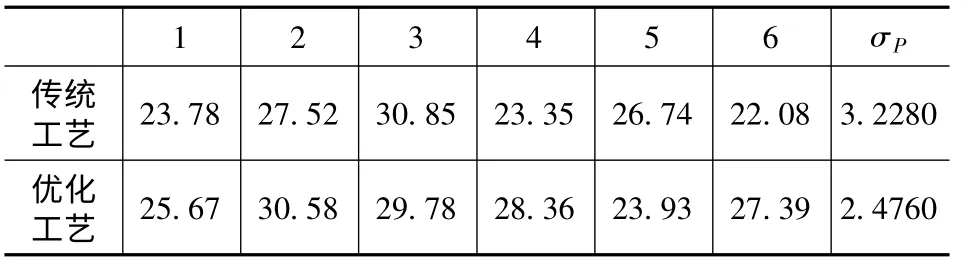
表3 改进前后螺栓应力分布(单位MP)

由σP值可知，改进后工艺各螺栓周围平均应力标准差由3.2280 下降到2.4760，结合面应力分布更加均匀，达到了一定优化效果。

将力转换回力矩，得到优化后拧紧工艺为:12.0N·m 第一次初始预紧→32N·m 第一次补充加载→保持45 分钟→卸载→10.3N·m 第二次初始预紧→28N·m 第二次补充加载。

4 结论

运用ANSYS 建立某型发动机盘式连接螺栓组有限元模型，用APDL 语言编写载荷分步加载程序，模拟载荷分步加载全过程。通过提取的对角拧紧和顺序拧紧两组分步加载数据表明:

(1)分步加载可以使螺栓组各螺栓间残余预紧力相差减小，使结合面应力分布更加均匀，从而提高螺栓组的连接性能。

(2)当分步数小于5 时改善效果明显，当分步数超过5 时，改善效果不再明显，螺栓残余预紧力和结合面面压趋于稳定，因此，过细的分步是没有必要的，一般取3 ～5 即可。

(3)根据仿真得到的结论，对发动机盘式连接螺栓组现有拧紧工艺进行优化，通过有限元仿真得到，优化后的拧紧工艺使各螺栓之间受力更加均衡，结合面应力分布更均匀，对装配连接工艺设计具有一定的指导意义。

［1］BibelG，EzellRAn Improved Flange Bolt－up Procedure Using Experimentally Determined Elastic Interaction Coefficient［J］Journal of Pressure Vessel Technology (ASME)1992，114(3):439－443.

［2］Toshimichi Fukuoka. Finite Element Simulation of Bolt－Up Process of Pipe Flange Connections［J］. Transactions of the ASME.2001，123(5):282－286.

［3］Toshimichi Fukuoka. Finite Element Simulation of Bolt－Up Process of Pipe Flange Connections With Spiral Wound Gasket［J］. Journal of Pressure Vessel Technology (ASME).2003，125(4):371－378.

［4］A.S. Nassar，S. Ganeshmurthy，R. M. Ranganathan，Gary C.Barbe. Effect of Tightening Speed on the Torque－Tension and Wear Pattern in Bolted Connections［J］. Transactions of the ASME. 2007，129(13):426－439.

［5］AS.Nassar，A.A. Alkelani. Clamp Load Loss due to Elastic Interaction and Gasket Creep Relaxation in Bolted Joints［J］. Transactions of the ASME.2006，128(6):394－400.

［6］ A. Bouzid，A. Nechache. The modeling of bolted flange joints used with disc springs and tube spacers to reduce relaxation［J］. International Journal of Pressure Vessels and Piping. 2010(87):730－736.

［7］杨国庆，陈成军，等.面向结合面密封性能要求的装配连接工艺设计［J］.西安交通大学学报，2012，46(3):75－82.

［8］陈成军，杨国庆，等. 基于有限元法的螺栓组连接弹性相互作用研究［J］. 武汉理工大学学报，2011，30(10):131－135.

［9］朱正德，林湖. 扭矩一转角法拧紧工艺条件下的装配质量评价［J］. 轻型汽车技术，2004，181(9):28－29.

［10］秦树人. 机械工程测试原理及技术［M］. 重庆大学出版社，2002.