均质刚体转动惯量的几种算法
高彩云
(山西大同大学物理与电子科学学院,山西大同 037009)
惯性是物体的一种固有属性,它表现为物体对其运动状态变化的一种阻抗程度。当物体受力为零时,惯性表现为物体保持其原有的静止或匀速直线运动状态;当物体受力不为零时,惯性表现为外力改变其原有运动状态的难易程度。物体的运动分为平动和转动,物体平动时表现出的惯性大小用物体的质量来量度,质量越大,平动惯性越大;物体转动时表现出的惯性大小用物体的转动惯量来量度,转动惯量越大,转动惯性越大。[1-3]
任何物体在受外力作用时都会发生形变,但如果形变的程度相对于物体本身线度来说极为微小,或者物体的形变不影响所研究的问题时,就可将形变忽略不计,把物体视为刚体。刚体转动惯量是刚体转动特性的一个重要的物理量,它的大小取决于物体的形状、质量分布及转轴的位置,而与其绕轴转动的角速度无关。刚体转动惯量的计算一直备受关注,目前已有不少文献对其进行了研究。对于形状不规则或非均质刚体的转动惯量,一般采用实验的方法进行测定,而对于形状规则的均质刚体,其转动惯量可直接利用公式计算。在大学物理教材中是通过微积分的方法,结合平行轴定理和垂直轴定理进行计算的。此外,还有质量投影法、量纲法、缩减法、等边n 角形极限法等。[4-10]本研究以几种常见的均质刚体为例,用不同的方法进行计算分析,有利于拓宽学生计算转动惯量的思路,并深刻理解刚体转动惯量的物理意义。
1 微元法
1.1 算法
转动惯量是刚体绕轴转动时惯性大小的量度,其定义式为:
式中,Δmi是刚体中某一质元的质量,ri是该质元到转轴的垂直距离,这里刚体中的质元是独立分布的。
对于质量连续分布的刚体,可以写成积分形式:
式中,dm是刚体中某一质元的质量,r是该质元到转轴的垂直距离,积分遍及整个刚体。在实际问题中,均匀刚体的质量可能是体分布(如均质正方体、圆柱体)、面分布(如均质圆盘)或线分布(如均质细棒),故质元的质量dm=ρdV=σds=λdl,式中ρ、σ、λ分别表示刚体的体密度、面密度和线密度。
1.2 算例
1.2.1 均质刚性杆的转动惯量
设质量均匀分布的刚性杆质量为m,长为l,绕z轴转动,如图1所示。
由图1 知,刚性杆上的质元是连续分布的,利用微元法计算时,可将刚性杆分割成无数个长为dx的微元,质量为dm,可视为质点,该微元到z轴的距离都为x,则该质元绕z轴转动的转动惯量为dI=x2dm,设刚性杆的线密度为λ,则dm=λdx,则刚性杆绕z轴转动的转动惯量为:
又知z′轴与z 轴的距离为,则由平行轴定理可得,刚性杆绕z′轴转动的转动惯量为:
可见,当刚体形状和质量分布不变时,其转动惯量和转轴的位置有关,且过质心轴线转动时的转动惯量最小。
1.2.2 均质圆盘的转动惯量
设质量均匀分布的圆盘质量为m,半径R,厚度不计,绕过圆心且垂直于盘面的o轴转动,如图2所示。
由图2 知,均质圆盘上的质元是连续分布的,利用微元法计算时,可将圆盘分割为无数个半径为r,宽为dr的薄圆环。设圆盘的面密度为σ,则dm=σ·2πrdr,圆环绕中心o轴转动的转动惯量dI=r2dm=r2·σ·2πrdr,则圆盘绕中心o轴线转动的转动惯量为:
这里也可以将圆盘分割成长rdθ,宽为dr的小面元,积分将转化为二重积分,计算较为复杂。故将圆盘分割成一系列的圆环,根据转动惯量的定义,圆环上各点到中心轴的距离都相等,只需沿着半径方向进行一重积分。
2 质量投影法
2.1 算法
由转动惯量的定义I=可知,若质元到刚体转轴的距离保持不变,则对该转轴的转动惯量就不变。由此可引入质量投影法:将刚体上各质元向垂直于转轴的平面投影,保持总质量不变,得到新的刚体,转动惯量不变。这样,可将三维刚体转化为与其转动惯量相等的二维刚体,同理,将二维刚体转化为与其转动惯量相等的一维刚体。
2.2 算例
2.2.1 均质矩形板的转动惯量
设质量均匀分布的矩形板质量为m,长为a、长为b,厚度不计,绕y轴转动,如图3所示。
根据质量投影法,把矩形板投影到与y轴垂直的平面,总质量保持不变,这样将二维刚体(矩形板)转化成一维刚体(刚性杆),它们绕y轴转动的转动惯量相等,那么,只需要计算刚性杆绕y轴转动的转动惯量。
依据上述微元法可得刚性杆绕y轴转动的转动惯量为Iy=,故矩形板绕y轴转动的转动惯量也为Iy=,同理可得,矩形板绕x轴转动的转动惯量也为Ix=。此方法计算简便,但是需要已知均质刚性杆绕轴转动的转动惯量。
2.2.2 长方体的转动惯量
设质量均匀分布的长方体质量为m,棱长分别为a、b、c,绕z轴转动,如图4所示。
根据质量投影法,把长方体投影到与z轴垂直的平面,总质量保持不变,这样将三维刚体(长方体)转化成二维刚体(矩形板),它们绕z轴转动的转动惯量相等,那么,只需要计算矩形板绕z轴转动的转动惯量。
由垂直轴定理,矩形板对z轴的转动惯量为Iz=Ix+Iy=,则长方体对z轴的转动惯量也为。显然,此方法计算简便,但是需要已知均质矩形板绕轴转动的转动惯量。
2.2.3 均质圆柱体的转动惯量
设质量均匀分布的圆柱体质量为m,半径为R,绕z轴转动,如图5所示。
根据质量投影法,把圆柱体投影到与z轴垂直的平面,总质量保持不变,这样将三维刚体(圆柱体)转化成二维刚体(圆盘),它们绕z轴转动的转动惯量相等,那么,只需要计算矩形板绕z轴转动的转动惯量。
由微元法可知,圆盘绕z 轴的转动惯量为Iz=,则长圆柱体对z轴的转动惯量也为。用此方法计算需要已知圆盘绕过中心且垂直于盘面轴转动的转动惯量。
3 缩减法
3.1 算法
转动惯量的量纲是ML2,引入无量纲常数k,设m为物体的质量,则一维物体的转动惯量可以表示为:
I=kmx2,
其中,x是物体的独立长度。
二维物体的转动惯量可表示为:
I=∑ikmxiy2-i,i∈R,
其中,x、y是物体的两个独立长度。
三维物体的转动惯量可表示为:
I=∑i∑jkmxiyjz2-i-j,(i,j)∈R2,
其中,x、y、z是物体的3个独立长度。
3.2 算例
3.2.1 均质等腰三角形的转动惯量
设质量均匀分布的等腰三角形质量为m,腰长为a、底边为b,绕垂直穿过其质心的o轴的转动,如图6所示。
等腰三角形是二维刚体,其惯量可写成I=∑ikmxiy2-i。现将其分割为4个全等的小等腰三角形,其质量、腰长、底边分别为。分割缩小后的4个小三角形腰长和底边都为原三角形的,缩放倍数n=,每个小三角形的o1轴与o轴的距离为,o2、o3轴与o轴的距离为,绕垂直穿过其新质心轴的转动惯量为。
原等腰三角形的转动惯量应为4个小等腰三角形相对于原转动o轴的转动惯量之和,根据平行轴定理,得:
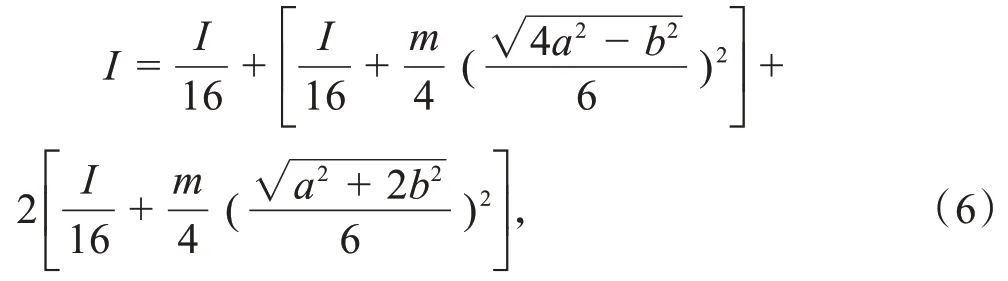
化简得:I=。
可知,等腰三角形绕质心o轴的转动惯量与其质量、底边和腰长有关。若三角形为等边三角形,则a=b,I=。
3.2.2 均质矩形板的转动惯量
设质量均匀分布的矩形板质量为m,长为a、长为b,厚度不计,绕垂直穿过其质心的o 轴的转动,如图7所示。
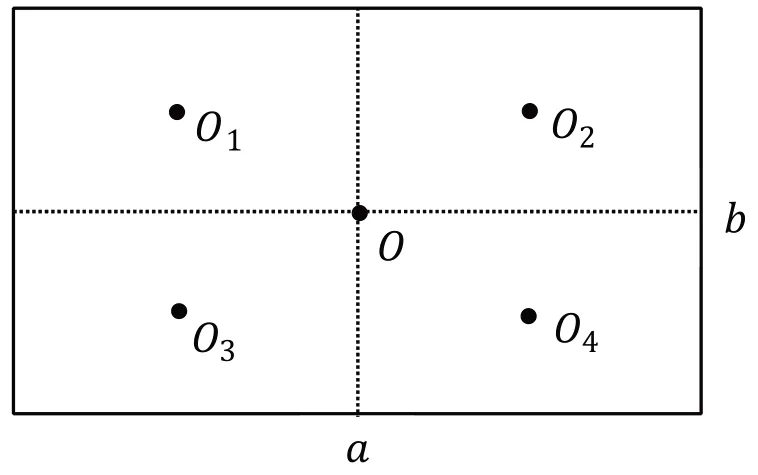
图7 等腰三角形绕质心轴转动
矩形板是二维刚体,其惯量可写成I=∑ikmxiy2-i。现将其分割为4个全等的小矩形,其质量、长、宽分别为。分割缩小后的4个小矩形的长和宽都为原矩形板的,缩放倍数n=,每个小矩形的新质心轴o1、o2、o3、o4与原质心o轴的距离为,o2、o3轴与o轴的距离为,绕垂直穿过其新质心轴的转动惯量为。
原矩形绕质心o轴的转动惯量应为4个小矩形绕o轴的转动惯量之和,根据平行轴定理,得:
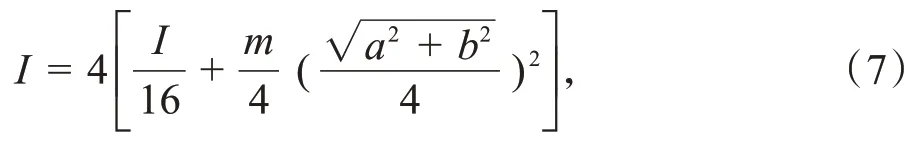
化简得I=。若是正方形,则a=b,I=。
3.2.3 长方体的转动惯量
设质量均匀分布的长方体质量为m,棱长分别为a、b、c,绕oo′轴转动,如图8所示。
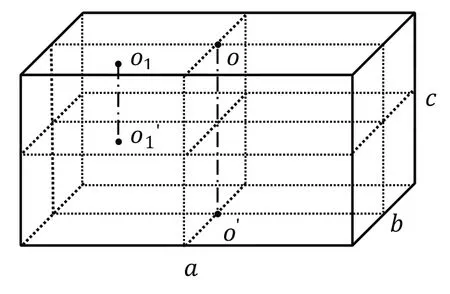
图8 长方体绕质心轴转动
长方体是三维刚体,其惯量可写成I=∑i∑jkmxiyjz2-i-j。现将其分割为8 个相同的小长方体,其质量和棱长分别为。分割缩小后的8 个小长方体的棱长都为原长方体的,缩放倍数n=,小长方体的新质心轴o1o1′与原质心轴oo′的距离为,绕垂直穿过其新质心轴的转动惯量为。
原长方体绕质心轴oo′的转动惯量应为8 个小长方体绕oo′轴的转动惯量之和,根据平行轴定理,得:
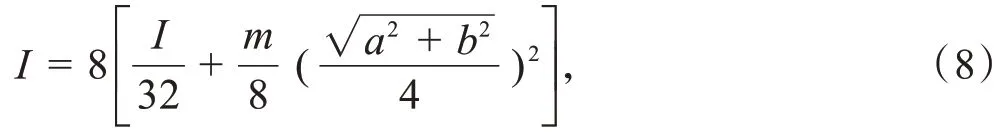
化简得I=。若是正方形,则a=b,I=。
4 结语
转动惯量是刚体转动惯性的量度,其大小与刚体质量分布及轴的位置有关,质元的质量越大,质元到轴的距离越大,其转动惯量就越大。从刚体转动惯量的定义出发,分别采用微元法、质量投影法和缩减法计算了刚性杆、圆盘、三角形、长方形、长方体和圆柱体的转动惯量。通过计算可得,微元法积分法易于理解,但只能计算形状规则的均质刚体的转动惯量,对于形状不规则、质量分布不均匀的刚体,涉及到复杂的积分运算,故运用较少;质量投影法是根据转动惯量的定义推导而得,已于理解,可将问题化简,但是需要已知投影之后刚体的转动惯量;缩减法是将刚体按比例放大或缩小,引入无量纲常数,计算时需要结合平行轴定理,对于简单的问题不能简便,但可以拓展思路。

