加强初中数学建模教学 培养学生应用数学意识

和恒环

摘 要:通过对新课改初中数学的教学和研究,结合新教材的编写特点,应对如何加强初中数学建模教学,培养学生应用数学的意识进行探索。

关键词:数学建模;应用意识;思想方法

中图分类号:G633.6 文献标识码:A 文章编号:1009-010X(2009)08-0049-02

全日制义务教育《数学课程标准》中指出:“数学教学就是让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生对数学理解的同时,在思维能力、情感态度、价值观等方面得到进步和发展。体会到数学就在身边,感受到数学的趣味和作用,体验到数学的魅力和应用。”课程标准将“发展学生的数学应用意识”作为主要理念之一,认为开展数学应用的教学活动符合社会需要,有利于激发学生学习数学的兴趣,有利于增强学生的应用意识,有利于扩展学生的视野。初中数学课程应提供基本内容的实际背景,反映数学的应用价值,开展“数学建模”的学习活动。从数学课程标准中我们看出数学建模已成为注重数学应用教学的主要思路和必然选择。

近年来数学建模的题目在中考试题中也逐渐增大了权重。中考试题加强了应用题的考查,这些应用题以数学建模为中心,考查学生应用数学的能力,但学生在应用题中的得分率远低于其他题目,原因之一就是学生缺乏数学建模能力和应用数学意识。因此,我们应加强数学建模的教学,提高学生数学建模能力,培养学生应用数学意识。那么在教学设计中如何渗透数学建模思想,如何开展数学建模的教学呢?本文结合教学实践,就如何加强初中数学建模教学谈几点体会。

一、掌握常见数学应用题的基本数学模型

在初中阶段通常通过建立几何图形、方程或不等式、函数、三角函数等数学模型来解应用题。通过这些应用题的教学渗透数学建模的思想与方法。

几何与人类生活和实际需要密切相关,诸如航海、建筑、测量、工程定位、裁剪方案、道路拱桥设计等涉及一定图形的性质时,常把实际问题转化为几何问题,通过建立几何模型来加以解决。建立几何模型可以使学生多方面全方位地感受数学建模过程,巩固数学建模思维。教学中对学生展示如下的建模过程:现实原型问题,数学抽象,简化原则,数学模型,演算推理,数学模型的解,现实原型问题的解,返回解释。

例:在一次数学综合实践活动课上,老师带领学生去测一条南北流向的河的宽度,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西经验45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度。(参考数值:tan31°≈3/5,sin31°≈1/2)

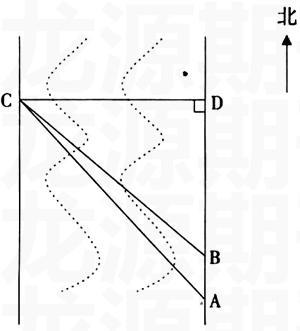
分析:本例题是把生活中常见的问题建立几何模型,然后利用三角函数来解答。

现实生活事物之间存在着广泛的联系,函数(方程、不等式)揭示了现实世界众多的数量关系及运动规律。运用函数(方程、不等式)解应用题体现了在数学建模思维过程要据所掌握的信息和背景材料,对问题加以变形,使其形简化,且解题过程中重要的步骤是据题意列出函数(方程、不等式),从而使学生明白,数学建模过程的重点及难点就是据实际问题的特点,通过观察、类比、归纳、分析、概括等基本思想,联想现成的数学模型或变换问题构造新的数学模型来解决问题。如利息(复利)的数列模型、利润计算的方程模型,决策问题的函数模型以及不等式模型等。

例:一家用电器开发公司研制出一种新型电子产品,每件的生产成本为20元,按定价60元出售,每月可销售20万件。为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件。

(1)求出月销售量y(万件)与销售单价x(元)之间的函数关系式(不必写的取值范围);

(2)求出月销售利润z(万元)(利润=售价-成本价)与销售单价x(元)之间的函数关系式(不必写的取值范围);

(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于1200万元。

分析:这属于计划决策问题,问题的关键是找到月销售利润与销售单价之间的函数关系式,建立函数模型,最后将问题转化为求满足条件的函数自变量x取值范围的问题。解(略)。

总之,我认为在实际教学中做好常见应用题数学建模的教学,要弹奏好以下四步曲:

1.要认真审题。

建立数学模型,首先要认真审题。实际应用题的题目一般都比较长,涉及的名词、概念较多,因此要耐心细致地读题,深刻分解实际问题的背景,明确建模的目的;弄清问题中的主要已知事项,尽量掌握建模对象的各种信息;挖掘实际问题的内在规律,明确所求结论和对所求结论的限制条件。

2.要进行必要简化。

根据实际问题的特征和建模的目的,对问题进行必要简化。抓住主要因素,抛弃次要因素,根据数量关系,联系数学知识和方法,用精确的语言作出假设。

3.抽象。

将已知条件与所求问题联系起来,恰当引入参数变量或适当建立坐标系,将文字语言翻译成数学语言,将数量关系用数学式子、图形或表格等形式表达出来,从而建立数学模型。

4.数学模型求解、寻找现实原型问题的解,返回解释。

数学模型求解也是很关键的一步,如果不能用数学方法正确求解的话,就不能让数学回归至正确解决实际问题,所有的工作将是功亏一篑,所以要让学生掌握数学模型的简捷快速高效的求解方法。

完成模型求解之后,我们还需要验证求解数据对解决实际问题的合理性和适用性,找到实际应用题的解。显然,这一步是非常重要的,并且是必不可少的。这一步是体现数学应用价值的非常重要的一个环节,也是培养学生数学应用意识的最重要的一个环节。

二、数学建模教学要重视知识产生和发展过程

由于知识产生和发展过程本身就蕴含着丰富的数学建模思想,因此教师既要重视实际问题背景的分析、参数的简化、假设的约定,还要重视分析数学模型建立的原理与过程,数学知识、方法的转化与应用,不能仅仅讲授数学建模结果,忽略数学建模的过程。

三、鼓励学生积极主动地参与,把教学过程更自觉地变成学生活动的过程

数学应用与数学建模的目的并不是仅仅为了解决一些具体问题,而是要培养学生的应用意识、数学能力和数学素质。因此我们不应该沿用老师讲题、学生模仿练习的套路,而应该重过程、重参与,更多地表现活动的特性。

四、注意结合学生的实际水平,分层次逐步地推进数学建模的教学

数学建模对教师对学生都有一个逐步的学习和适应的过程。教师在数学建模教学实践中,特别应考虑学生的实际能力和水平,起始点要低,形式多样有利于更多的学生参与。在开始的教学中,在讲解知识的同时有意识地介绍知识的应用背景。在应用的重点环节结合比较多的训练,逐步扩展到让学生用已有的数学知识解释一些实际结果,描述一些实际现象,模仿地解决一些比较确定的应用问题,到独立地运用数学建模的方法解决教师提供的数学应用问题,最后发展成能独立地发现、提出一些实际问题,并能用数学建模的方法解决它。

加强初中数学建模教学,培养学生应用数学的意识,重要的是在教学中坚持以学生为主体。让学生感受到学数学是为了用数学,数学就在我们的身边,从而体验数学的应用价值,自觉地在学习过程中构建和应用数学模型意识。

参考文献:

[1]教育部.全日制义务教育数学课程标准(实验稿)[M].2001,7.

[2]冯永明.中学数学建模的教学构想与实践[J].数学通讯,2000,7.

【责任编辑 姜华】